距離度量以及python實現(二)
接上一篇:http://www.cnblogs.com/denny402/p/7027954.html
7. 夾角余弦(Cosine)
也可以叫余弦相似度。 幾何中夾角余弦可用來衡量兩個向量方向的差異,中借用這一概念來衡量樣本向量之間的差異。
(1)在二維空間中向量A(x1,y1)與向量B(x2,y2)的夾角余弦公式:
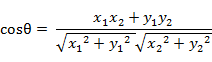
(2) 兩個n維樣本點a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夾角余弦
類似的,對於兩個n維樣本點a(x11,x12,…,x1n)和b(x21,x22,…,x2n),可以使用類似於夾角余弦的概念來衡量它們間的相似程度。
即:
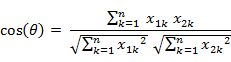
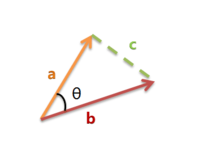
余弦取值範圍為[-1,1]。求得兩個向量的夾角,並得出夾角對應的余弦值,此余弦值就可以用來表征這兩個向量的相似性。夾角越小,趨近於0度,余弦值越接近於1,它們的方向更加吻合,則越相似。當兩個向量的方向完全相反夾角余弦取最小值-1。當余弦值為0時,兩向量正交,夾角為90度。因此可以看出,余弦相似度與向量的幅值無關,只與向量的方向相關。
import numpy as np x=np.random.random(10) y=np.random.random(10) #方法一:根據公式求解 d1=np.dot(x,y)/(np.linalg.norm(x)*np.linalg.norm(y))#方法二:根據scipy庫求解 from scipy.spatial.distance import pdist X=np.vstack([x,y]) d2=1-pdist(X,‘cosine‘)
兩個向量完全相等時,余弦值為1,如下的代碼計算出來的d=1。
d=1-pdist([x,x],‘cosine‘)
8. 皮爾遜相關系數(Pearson correlation)
(1) 皮爾遜相關系數的定義
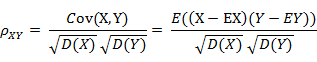
前面提到的余弦相似度只與向量方向有關,但它會受到向量的平移影響,在夾角余弦公式中如果將 x 平移到 x+1, 余弦值就會改變。怎樣才能實現平移不變性?這就要用到皮爾遜相關系數
如果將夾角余弦公式寫成:
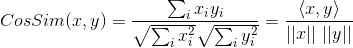
表示向量x和向量y之間的夾角余弦,則皮爾遜相關系數則可表示為:
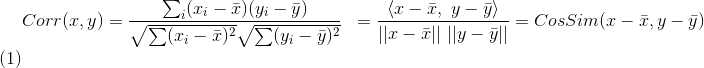
皮爾遜相關系數具有平移不變性和尺度不變性,計算出了兩個向量(維度)的相關性。
在python中的實現:
import numpy as np x=np.random.random(10) y=np.random.random(10) #方法一:根據公式求解 x_=x-np.mean(x) y_=y-np.mean(y) d1=np.dot(x_,y_)/(np.linalg.norm(x_)*np.linalg.norm(y_)) #方法二:根據numpy庫求解 X=np.vstack([x,y]) d2=np.corrcoef(X)[0][1]
相關系數是衡量隨機變量X與Y相關程度的一種方法,相關系數的取值範圍是[-1,1]。相關系數的絕對值越大,則表明X與Y相關度越高。當X與Y線性相關時,相關系數取值為1(正線性相關)或-1(負線性相關)。
9. 漢明距離(Hamming distance)
(1)漢明距離的定義
兩個等長字符串s1與s2之間的漢明距離定義為將其中一個變為另外一個所需要作的最小替換次數。例如字符串“1111”與“1001”之間的漢明距離為2。
應用:信息編碼(為了增強容錯性,應使得編碼間的最小漢明距離盡可能大)。
在python中的實現:
import numpy as np from scipy.spatial.distance import pdist x=np.random.random(10)>0.5 y=np.random.random(10)>0.5 x=np.asarray(x,np.int32) y=np.asarray(y,np.int32) #方法一:根據公式求解 d1=np.mean(x!=y) #方法二:根據scipy庫求解 X=np.vstack([x,y]) d2=pdist(X,‘hamming‘)
10. 傑卡德相似系數(Jaccard similarity coefficient)
(1) 傑卡德相似系數
兩個集合A和B的交集元素在A,B的並集中所占的比例,稱為兩個集合的傑卡德相似系數,用符號J(A,B)表示。
![]()
傑卡德相似系數是衡量兩個集合的相似度一種指標。
(2) 傑卡德距離
與傑卡德相似系數相反的概念是傑卡德距離(Jaccard distance)。傑卡德距離可用如下公式表示:
![]()
傑卡德距離用兩個集合中不同元素占所有元素的比例來衡量兩個集合的區分度。
(3) 傑卡德相似系數與傑卡德距離的應用
可將傑卡德相似系數用在衡量樣本的相似度上。
樣本A與樣本B是兩個n維向量,而且所有維度的取值都是0或1。例如:A(0111)和B(1011)。我們將樣本看成是一個集合,1表示集合包含該元素,0表示集合不包含該元素。
在python中的實現:
import numpy as np from scipy.spatial.distance import pdist x=np.random.random(10)>0.5 y=np.random.random(10)>0.5 x=np.asarray(x,np.int32) y=np.asarray(y,np.int32) #方法一:根據公式求解 up=np.double(np.bitwise_and((x != y),np.bitwise_or(x != 0, y != 0)).sum()) down=np.double(np.bitwise_or(x != 0, y != 0).sum()) d1=(up/down) #方法二:根據scipy庫求解 X=np.vstack([x,y]) d2=pdist(X,‘jaccard‘)
11. 布雷柯蒂斯距離(Bray Curtis Distance)
10. 卡方距離(Ki-square Distance)
距離度量以及python實現(二)
