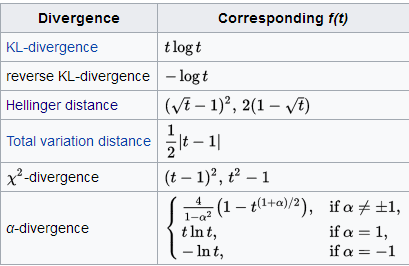
1、f 散度（f-divergence)

KL-divergence 的壞處在於它是無界的。事實上KL-divergence 屬於更廣泛的 f-divergence 中的一種。

如果P和Q被定義成空間中的兩個概率分佈，則f散度被定義為：

一些通用的散度，如KL-divergence, Hellinger distance, 和total variation distance，都是f散度的一種特例。只是f函式的取值不同而也。

在python中的實現 ：

import numpy as np
import scipy.stats
 
p=np.asarray([0.65,0.25,0.07,0.03])
q
 
=np.array([0.6,0.25,0.1,0.05])

def f(t):
    return t*np.log(t)
    
#方法一：根據公式求解
f1=np.sum(q*f(p/q))

#方法二：呼叫scipy包求解
f2=scipy.stats.entropy(p, q) 

2、Hellinger distance

1 定義

  1.1 度量理論

    為了從度量理論的角度定義Hellinger距離，我們假設P和Q是兩個概率測度，並且它們對於第三個概率測度λ來說是絕對連續的，則P和Q的Hellinger距離的平方被定義如下：

這裡的dP / dλ

  1.2 基於Lebesgue度量的概率理論

    為了在經典的概率論框架下定義Hellinger距離，我們通常將λ定義為Lebesgue度量，此時dP / dλ 和 dQ / dλ就變為了我們通常所說的概率密度函式。如果我們把上述概率密度函式分別表示為 f 和 g ，那麼可以用以下的積分形式表示Hellinger距離：

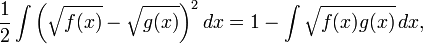
上述等式可以通過展開平方項得到，注意到任何概率密度函式在其定義域上的積分為1。

根據柯西-施瓦茨不等式（Cauchy-Schwarz inequality），Hellinger距離滿足如下性質：

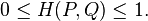
  1.3 離散概率分佈

對於兩個離散概率分佈 P=(p1,p2,...,pn)和 Q=（q1,q2,...,qn)，它們的Hellinger距離可以定義如下：

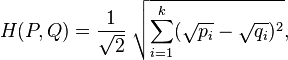
上式可以被看作兩個離散概率分佈平方根向量的歐式距離，如下所示：

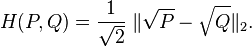
也可以寫成：

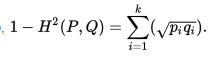
在python中的實現：

import numpy as np
 
p=np.asarray([0.65,0.25,0.07,0.03])
q=np.array([0.6,0.25,0.1,0.05])

#方法一：
h1=1/np.sqrt(2)*np.linalg.norm(np.sqrt(p)-np.sqrt(q))

#方法二：
h2=np.sqrt(1-np.sum(np.sqrt(p*q)))

3、巴氏距離（Bhattacharyya Distance）

在統計中，Bhattacharyya距離測量兩個離散或連續概率分佈的相似性。它與衡量兩個統計樣品或種群之間的重疊量的Bhattacharyya係數密切相關。Bhattacharyya距離和Bhattacharyya係數以20世紀30年代曾在印度統計研究所工作的一個統計學家A. Bhattacharya命名。同時，Bhattacharyya係數可以被用來確定兩個樣本被認為相對接近的，它是用來測量中的類分類的可分離性。

對於離散概率分佈 p和q在同一域 X，巴氏距離被定義為：

其中BC(p,q)是Bhattacharyya係數：

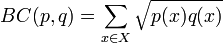
對於連續概率分佈，Bhattacharyya係數被定義為：

從公式可以看出，Bhattacharyya係數BC(P,Q)可以和前面的Hellinger距離聯絡起來，此時Hellinger距離可以被定義為：

因此，求得巴氏係數之後，就可以求得巴氏距離和Hellinger距離。

在python中的實現：

import numpy as np
 
p=np.asarray([0.65,0.25,0.07,0.03])
q=np.array([0.6,0.25,0.1,0.05])

BC=np.sum(np.sqrt(p*q))

#Hellinger距離：
h=np.sqrt(1-BC)

#巴氏距離：
b=-np.log(BC)

4、MMD距離（Maximum mean discrepancy)

最大均值差異（Maximum mean discrepancy），度量在再生希爾伯特空間中兩個分佈的距離，是一種核學習方法。兩個隨機變數的距離為：

其中k(.)是對映，用於把原變數對映到高維空間中。X,Y表示兩種分佈的樣本，F表示對映函式集。

基於兩個分佈的樣本，通過尋找在樣本空間上的對映函式K，求不同分佈的樣本在K上的函式值的均值，通過把兩個均值作差可以得到兩個分佈對應於K的mean discrepancy。尋找一個K使得這個mean discrepancy有最大值，就得到了MMD。最後取MMD作為檢驗統計量（test statistic），從而判斷兩個分佈是否相同。如果這個值足夠小，就認為兩個分佈相同，否則就認為它們不相同。更加簡單的理解就是：求兩堆資料在高維空間中的均值的距離。

近年來，MMD越來越多地應用在遷移學習中。在遷移學習環境下訓練集和測試集分別取樣自分佈p和q，兩類樣本集不同但相關。我們可以利用深度神經網路的特徵變換能力，來做特徵空間的變換，直到變換後的特徵分佈相匹配，這個過程可以是source domain一直變換直到匹配target domain。匹配的度量方式就是MMD。

在python中的實現，根據核函式不同，公式可能不一樣，根據公式程式設計即可。

5、Wasserstein distance

Wasserstein 距離，也叫Earth Mover's Distance，推土機距離，簡稱EMD，用來表示兩個分佈的相似程度。

Wasserstein distance 衡量了把資料從分佈“移動成”分佈時所需要移動的平均距離的最小值（類似於把一堆土從一個形狀移動到另一個形狀所需要做的功的最小值）

EMD是2000年IJCV期刊文章《The Earth Mover's Distance as a Metric for Image Retrieval》提出的一種直方圖相似度量（作者在之前的會議論文中也已經提到，不過鑑於IJCV的權威性和完整性，建議參考這篇文章）。

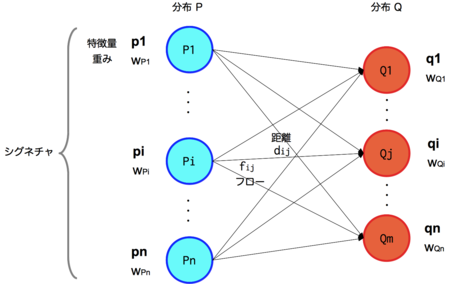
假設有兩個工地P和Q，P工地上有m堆土，Q工地上有n個坑，現在要將P工地上的m堆土全部移動到Q工地上的n個坑中，所做的最小的功。

每堆土我們用一個二元組來表示(p,w)，p表示土堆的中心，w表示土的數量。則這兩個工地可表示為：

每個土堆中心pi到每個土坑中心qj都會有一個距離dij，則構成了一個m*n的距離矩陣。

那麼問題就是我們希望找到一個流（flow），當然也是個矩陣[fij]，每一項fij代表從pi到qj的流動數量，從而最小化整體的代價函式：

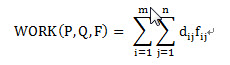
問題描述清楚了：就是把P中的m個坑的土，用最小的代價搬到Q中的n個坑中，pi到qj的兩個坑的距離由dij來表示。fij是從pi搬到qj的土的量；dij是pi位置到qj位置的代價（距離）。要最小化WORK工作量。EMD是把這個工作量歸一化以後的表達，即除以對fij的求和。

 EMD公式：

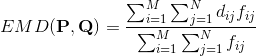
更多關於EMD的理解請參考：

 在python中的實現：呼叫opencv

import numpy as np
import cv

#p、q是兩個矩陣，第一列表示權值，後面三列表示直方圖或數量
p=np.asarray([[0.4,100,40,22],
            [0.3,211,20,2],
            [0.2,32,190,150],
            [0.1,2,100,100]],np.float32)
q=np.array([[0.5,0,0,0],
            [0.3,50,100,80],
            [0.2,255,255,255]],np.float32)
pp=cv.fromarray(p)
qq=cv.fromarray(q)
emd=cv.CalcEMD2(pp,qq,cv.CV_DIST_L2)

 最後計算出來的emd:

emd = 160.542770