適用範圍：給你一個大數n，將它分解它的質因子的乘積的形式。

P.S. 在下面的論述中會使用到Miller_rabin和快速乘法和快速冪，如果有興趣請看另一篇博文。

不過其實你只需要知道Miller_rabin是判斷一個數是否是素數。q_mul是求（a*b）% mod，q_pow是求(a^b) % mod即可。

大數分解最簡單的思想也是試除法，這裡就不再展示程式碼了，就是從2到sqrt(n)，一個一個的試驗，直到除到1或者迴圈完，最後判斷一下是否已經除到1了即可。

但是這樣的做的複雜度是相當高的。一種很妙的思路是找到一個因子（不一定是質因子），然後再一路分解下去。這就是基於Miller_rabin的大數分解法Pollard_rho大數分解。

Pollard_rho演算法的大致流程是 先判斷當前數是否是素數（Miller_rabin）了，如果是則直接返回。如果不是素數的話，試圖找到當前數的一個因子（可以不是質因子）。然後遞迴對該因子和約去這個因子的另一個因子進行分解。

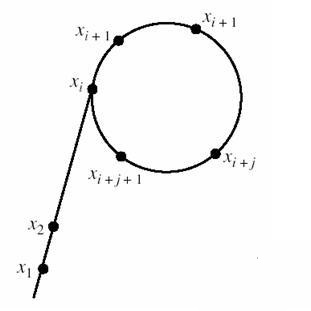
那麼自然的疑問就是，怎麼找到當前數n的一個因子？當然不是一個一個慢慢試驗，而是一種神奇的想法。其實這個找因子的過程我理解的不是非常透徹，感覺還是有一點兒試的意味，但不是盲目的列舉，而是一種隨機化演算法。我們假設要找的因子為p，他是隨機取一個x1，由x1構造x2，使得｛p可以整除x1-x2 && x1-x2不能整除n｝則p=gcd（x1-x2，n

因為x1和x2再調整時最終一定會出現迴圈，形成一個類似希臘字母rho的形狀，故因此得名。

另外通過find函式來分解素數，如果找到了一個素數因子則加入到因子map中，否則如果用Pollard找到一個因子則遞迴去找素數因子。

上程式碼：

#include <iostream> 
#include <cstdio> 
#include <algorithm>  
#include <cmath>  
#include <cstring>  
#include <map>  
using namespace std;

const int times = 50;
int number = 0;

map<long long, int>m;
long long Random( long long n )
{
	return ((double)rand( ) / RAND_MAX*n + 0.5);
}

long long q_mul( long long a, long long b, long long mod ) //快速乘法取模
{
	long long ans = 0;
	while(b)
	{
		if(b & 1)
		{
			ans += a;
		}
		b /= 2;
		a = (a + a) % mod;

	}
	return ans;
}

long long q_pow( long long a, long long b, long long mod ) //快速乘法下的快速冪，叼
{
	long long ans = 1;
	while(b)
	{
		if(b & 1)
		{
			ans = q_mul( ans, a, mod );
		}
		b /= 2;
		a = q_mul( a, a, mod );
	}
	return ans;
}

bool witness( long long a, long long n )//miller_rabin演算法的精華
{
	long long tem = n - 1;
	int j = 0;
	while(tem % 2 == 0)
	{
		tem /= 2;
		j++;
	}
	
	long long x = q_pow( a, tem, n ); //得到a^(n-1) mod n
	if(x == 1 || x == n - 1) return true;
	while(j--)
	{
		x = q_mul( x, x, n );
		if(x = n - 1) return true;
	}
	return false;
}

bool miller_rabin( long long n )  //檢驗n是否是素數
{

	if(n == 2)
		return true;
	if(n < 2 || n % 2 == 0)
		return false;

	for(int i = 1; i <= times; i++)  //做times次隨機檢驗
	{
		long long a = Random( n - 2 ) + 1; //得到隨機檢驗運算元 a
		if(!witness( a, n ))  //用a檢驗n是否是素數
			return false;
	}
	return true;
}

long long gcd( long long a, long long b )
{
	if(b == 0)
		return a;
	return gcd( b, a%b );
}

long long pollard_rho( long long n, long long c )//找到n的一個因子
{
	long long x, y, d, i = 1, k = 2;
	x = Random( n - 1 ) + 1;
	y = x;
	while(1)
	{
		i++;
		x = (q_mul( x, x, n ) + c) % n;
		d = gcd( y - x, n );
		if(1<d&&d<n)
			return d;
		if(y == x)//找到迴圈，選取失敗，重新來
			return n;
		if(i == k) //似乎是一個優化，但是不是很清楚
		{
			y = x;
			k <<= 1;
		}
	}
}

void find( long long n, long long c )
{
	if(n == 1)
		return;
	if(miller_rabin( n ))
	{
		m[n]++;
		number++;
		return;
	}

	long long p = n;
	while(p >= n)
		p = pollard_rho( p, c-- );
	find( p, c );
	find( n / p, c );
}

int main( )
{
	long long tar;
	while(cin >> tar)
	{
		number = 0;
		m.clear();
		find( tar, 2137342 );
		printf( "%lld = ", tar );
		if(m.empty())
		{
			printf( "%lld\n", tar );
		}
		for(map<long long, int>::iterator c = m.begin(); c != m.end();)
		{
			printf( "%lld^%d", c->first, c->second );
			if((++c) != m.end())
				printf( " * " );
		}
		printf( "\n" );
	}
	return 0;
}