行列式：

   排列：由自然陣列成的有序陣列；

   逆序：前後位置與大小順序相反，即：    ,記作： ;     排列中，逆序的總數稱為逆序數；

   奇偶排列： 若排列的逆序數 為奇， 則為 奇排列；   偶排列同理可得；

   行列式： ， 其中第一個下標指行，第二個下標指 列；

   n階行列式：列標的逆序數為偶時，係數為正；  列標的逆序數為 奇 時，係數為負；

   三階行列式的演算法:

         每一項均由  取自 不同行， 不同列 的三個元素的 乘積 構成項數 為 n 的 階乘；

   n階行列式的演算法：

          

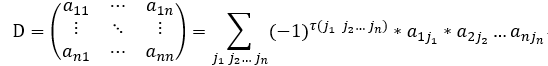
     上三角行列式： 其值 等於 其主對角線 上 各元素 的乘積；

                    若主對角線 為：  "  / " , 則 

轉置行列式：

       定義： 將行列式  的 行  轉化為 相應列，記為：;

       性質：

            1. 行列式  與 它的轉置 行列式 相等；（數值）；

            2.  互換  行列式的兩行 或者 列，行列式值變好；

                      推論： 託行列式兩行（列） 完全相同，則 D =0；

            3.  行列式中   某 行(列) 的所有元素的 公因子 可 提到行列式 符號的外面。 即  

                     推論：  D 中 行（列） 所有元素 為0  ，則 D =0；

                                  D 中 兩行（列） 對應元素成比例，則 D =0；

            4. 若 D中  某行 （列） 都是兩數之和，則可以分解，即：

                     

            5. 行列式 某一行（列） 的所有元素 都乘以 K, 再 加到 另一行（列）的相應元素上，行列式值不變，即：

                      

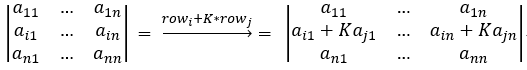
餘子式與 代數餘子式：

       餘子式定義：  (n-1)階行列式，稱為： 的餘子式，記為： 

       代數餘子式：

               

       展開定理1：

                n階行列式 = 它的任一 行（列）的各元素  與 其對應的 代數餘子式的乘積 之和；

        展開定理2：

                n階行列式 中 某一 元素  乘以 其它元素的代數餘子式 之和 為零；

        範德蒙行列式：

                  ， 其表示： 所有可能的乘積；

矩陣：

      定義：  由 m*n 個數  構成的 m 行 n 列 數列， 稱為 m行n列 矩陣；   記為：   或者

      方陣：由 n^2  個數 排成 的 n*n 矩陣，稱為 n階方陣；  記為：  

      單位矩陣：

              主對角線為1，其餘全為0 的矩陣；

      零矩陣：

               矩陣中所有元素都為0 的矩陣；

        注意： 矩陣式一個表，而不是數； 行列式 代表的是一個 數值；

        數量矩陣： 

                 n階對角矩陣  所有主對角線 元素相等 的 矩陣；

        三角矩陣：  包括 上三角矩陣；  下三角矩陣；

        對稱矩陣：

                 矩陣中 所有元素 關於主對角線 對稱 的矩陣；

        反對稱矩陣：

                  叫做 反對稱矩陣 （它們的主對角線元素 必須全為 零）；

                   注意： 兩個同階  反對稱矩陣  的乘積  不一定是反對稱；

        n階矩陣行列式:  

                    A 階方證 構成的行列式， 即為 |A|;

                    若  A 為 n階方陣，則 ： |2A| = 2^n * |A|;

         行階梯形矩陣：

                  1.零行（元素全為 零的 行） 位於 矩陣下方；

                  2.  各非零行的 首個 非零元素， 從左  往 右， 下方全為零；

          行最簡形矩陣：

                   1. 各非零行 的首個 非零元素 都是 1；

                   2. 每個首  非零元素  所在 的列 其餘元素 都 是 0；

           標準形矩陣：

                    1.  矩陣左上角 是單位陣；

                    2.  其餘元素都是0；

          矩陣化簡次序： 梯形 -->   最簡形 --->  標準形;

          奇異矩陣(退化矩陣)：  |A| =0；

          非奇異矩陣(非退化矩陣):  |A| =/=0;

矩陣的運算：

      相等： 矩陣行 列 相等，且 元素 一毛一樣；

      加法，減法，數乘，數乘和：  略；

      矩陣乘法：

            前提： A 的行  與 B 的列相同；

            A*B 的行 = A 的行；

            A*B 的 列 = B 的列；

            A*B =/= B*A;

            兩個非零 矩陣 的乘積 可能為 零矩陣；

           eg:              

       冪運算：

            

        轉置：

              規則：   ； 

                          ；  

                          

                           

矩陣的初等變換：

     1.交換 矩陣的兩行（列）；

     2. 以一個非 零 數 k 乘以 矩陣的 某一行（列）；

     3. 將矩陣 的 某一 行（列） 乘以k倍後 加到另一 行（列） 上；

逆矩陣：

        定義：

               n 階方陣 A ， 如存在 n階方陣 B ， st :   AB = BA = E, 則 A 可逆， 方陣B 稱為 A 的逆矩陣， 記為: ;

             n階方陣的逆矩陣 也為 n 階 方陣， 且是 唯一的， 逆矩陣的逆  是其本身；

         求逆矩陣的方法：

              1. 利用伴隨矩陣：

                   ，  

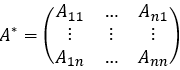
              2.利用初等變換：

                       = ===    

           性質：

               若A 可逆， 則  也可逆， 且 

               若A,B 均可逆 ， 則有：    （注意： ）

               若 |A| =/= 0 , 規定： ,

                

               

               ,λ，μ 為正整數；

           應用：

               A*x = B, 則 x = *B;

               x*A = B , 則 x = B* ;

               A*x * B = C , 則 x = *C*;

               A+Ax = Bx,  則 x = ;

               A+2x = Bx , 則 x = ;

         eg:  設方陣  A^2 -A -2E = 0 , 證明： A， A+2E 可逆；  且求出它們的逆矩陣；

             思路： A(A-E) =2E   1/2 *A* (A-E) =E,    A^ -1 = (A-E)/2