第二章 線性代數

2.1 名詞

標量（scalar）、向量（vector）、矩陣（matrix）、張量（tensor）

2.2 矩陣和向量相乘

1. 正常矩陣乘法； 2. 向量點積； 3. Hadamard乘積（元素對應乘積）

矩陣乘法服從分配律、結合律，兩個向量的點積滿足交換律，利用兩個向量點積的結果是標量（scalar），標量轉置是自身。

2.3 單位矩陣和逆矩陣

逆矩陣一般作為理論工具使用，計算機由於精度不足，一般不使用逆矩陣。

2.4 線性相關和生成子空間

線性方程組，解的個數：0、1、∞，不存在有限多個解的情況。

線性方程組，只有方陣，且是非奇異的（所有列向量線性無關）才能用逆矩陣求解。

2.5 範數(norm)

將向量對映到非負值的函式（衡量向量到原點的距離），滿足距離三要素。

範數分為x範數和L^x範數，例如L²被稱為歐幾里得範數。

L⁰範數（在數學意義上是不對的）：非零元素數目個數。

L¹範數：常用於資料集中於原點附近；零和非零元素差異非常重要；非零元素數目的替代函式（因為L⁰範數對向量縮放無感知）

L²範數：歐幾里得範數，其平方值常用於衡量向量的大小，可以簡單的通過點積運算。（在原點附近增長的十分緩慢，此時推薦用L¹範數）

L^∞範數：最大範數，最大的元素的絕對值，即||x||_∞=max_i(|x_i|)

Frobenius範數：常用於衡量矩陣的大小，在深度學習中的最常見做法，計算矩陣每個元素的平方和後 開方，類似於向量的L²

2.6 特殊型別的矩陣和向量

單位向量（unit vector）是具有單位範數（unit norm）的向量：||x||₂=1（歐幾里得距離為1）。

如果兩個向量不僅相互正交（點積為0）且範數為1，稱為標準正交（orthonormal）。

正交矩陣（orthogonal matrix）：行向量和列向量分別是標準正交的方陣。

2.7 特徵分解

將矩陣分解為特徵值 λ 和特徵向量的表示形式。（一般只有方陣才有）

可以看作在二維平面上畫出特徵向量後，乘上矩陣A表示這個向量被拉伸了 λ 倍，如下圖：

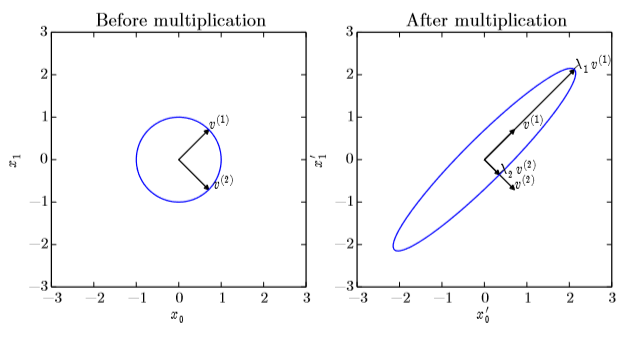
λ > 0：正定矩陣（positive definite）

λ ≥ 0：半正定矩陣（positive semidefinite）

λ < 0：負定矩陣（negative definite）

2.8 奇異值分解 SVD

這裡書裡講的不是很清楚，推薦一個視訊：https://www.bilibili.com/video/av15971352 

博主先在這裡說說自己對SVD的理解：就是

提取矩陣的特徵，按特徵的重要程度從大到小排序，每個特徵的權重就是奇異值，特徵本身就是奇異向量，當保留權重較大的幾個特徵時，能夠很好地還原出原矩陣。

因為非方陣的矩陣無法計算逆矩陣，所以無法進行特徵分解，故提出了奇異值分解（singular value decomposition）。

每個實數矩陣都有一個奇異值分解，但不一定都有特徵值分解。（例如，非方陣的矩陣沒有特徵分解，這時只能用奇異值分解）。

且奇異值分解有著更廣泛的應用（例如特徵降維，矩陣去噪）。

博主對原理的理解：SVD就是分別計算A^TA和AA^T，讓其變成方陣，然後對角化，從對角化後的資訊中提取特徵，經過轉換後作為奇異值，從而復原矩陣A。

2.9 Moore-Penrose偽逆（廣義逆矩陣）

A⁺=VD⁺U^T

U，D和V是矩陣A奇異值分解（SVD）後得到的矩陣，對角矩陣D的偽逆D⁺是其非零元素取倒數之後再轉置得到的。

當矩陣A的列數多於行數（矮胖）時，用偽逆求解線性方程是眾多可能解法中的一種。但是x=A⁺y是方程所有可行解中歐幾里得範數L²最小的一個。

當行數多於列數時，可能沒有解（因為沒有滿秩），在這種情況下，通過偽逆得到的x使得Ax和y的歐幾里得距離||Ax-y||₂最小。

（這部分沒怎麼查資料，暫時不知道其在機器學習中的應用）

2.10 跡運算

沒什麼好說的，對角線元素的和，以下是跡運算的性質：

一個矩陣的轉置不影響跡的大小；

多個矩陣相乘，將最後一個挪到最前面之後，跡是相同的（ Tr(ABC)=Tr(CAB)=Tr(BCA) ）。

標量在跡運算後仍然是它自己。a=Tr(a)；

迴圈置換後矩陣形狀變了，也不影響跡的大小。

2.11 行列式

det(A)等於矩陣特徵值的乘積，用來衡量矩陣參與矩陣乘法後空間擴大或者縮小了多少。

2.12 例項：主成分分析 PCA

關鍵詞：單位範數、L²範數、最優化問題、向量微積分、Frobenius範數……

這塊有點困難，之後補上。