Softmax是啥？

Hopfield網路的能量觀點

1982年的Hopfiled網路首次將統計物理學的能量觀點引入到神經網路中，

將神經網路的全域性最小值求解，近似認為是求解熱力學系統的能量最低點(最穩定點)。

為此，特地為神經網路定義了神經網路能量函式$E(x|Label)$，其中$x$為輸入。

$E(x|Label)=-\frac{1}{2}Wx \Delta Y  \quad where \quad \Delta Y=y-label$   (省略Bias項)

值得注意的是，這套山寨牌能量函式只能求出區域性最小值，SVM用二次規劃函式替換掉之後才能求全域性最小值。

唯一的敗筆是，Hopfiled網路的輸出仍然採用了階躍函式Sign，走的還是Rosenblatt的老路子。

這個能量函式非常有趣，它在階躍函式狀態下永遠是遞減的，即便是W永遠是正的。(錯誤的隨機初始化也是OK的)。

原因如下：

I、當階躍函式輸出為1時，Wx為正，若產生Loss，$\Delta Y=1-(-1)=2$，顯然$\Delta YE(x|y)$為負。

II、當階躍函式輸出為-1時，Wx為負，若產生Loss，$\Delta Y=-1-(1)=-2$，顯然$\Delta YE(x|y)$還是為負。

III、若無LOSS，$\Delta Y=1-1$或$(-1)-(-1)$都為0，$\Delta E(x|y)$也為0。

概率與Boltzmann機

祖師爺Hinton在1985年創立了第一個隨機神經網路，首次將概率引入神經網路這個大玄學中。

值得一提的是，在當時概率圖模型也是被公認為玄學之一，很多研究者認為，信概率還不如信神經網路。(今天倒是反過來了)

Boltzmann機延續了Hopfiled能量函式的傳統，但是用一個奇葩的歸一化函式來產生概率，以取代相對不精確的階躍函式。

這個歸一化函式描述如下：

$P(y)=\frac{1}{1+e^{\frac{-(Wx+b)}{T}}}$

其中T為溫度係數，超引數之一，需要調參。

看起來怎麼那麼眼熟呢，扔掉T之後，這不就是Sigmoid函式麼。

可以看到，Boltzmann機為了表達概率，選用了Sigmoid函式作為神經網路的概率平滑產生器。

多變數概率與限制Boltzmann機

1986年由Smolensky創立的限制Boltzmann機將Hopfiled網路的輸出部折回，這樣就產生了多變數的輸出。

如何去表達此時多變數情況下的概率，能量模型—配分函式(Partition Function)解決了這一點：

$P(x)=\frac{e^{-E(x)}}{Z}=\frac{e^{-E(x)}}{\sum _{i}e^{-E(i)}}$

配分項Z是大家耳熟能詳的噁心之物，它的求解讓深度學習推遲了20年。

在深度學習被卡的20年間，配分項函式在多變數的判別模型中廣泛推廣，疑似是Softmax的雛形。

EBM(Energy­Based Model)

在LeCun的EBM教程Slides的介紹了配分判別函式，也就是今天的Softmax函式。

★The partition function ensures that undesired answers are given low probability

★For learning, we need to approximate the partition function (or its gradient with respect to the parameters)

順便將其批判了一番：

★Max likelihood learning gives high probability to good answers

★Problem: there are too many bad answers!

這部分的觀點可以參照PRML的序章關於貝葉斯擬合學習的討論，採用配分判別的Loss、基於極大似然的頻統方法

非常容易產生過擬合和弱泛化，貝葉斯學習和深度學習則引入先驗Prior在極大似然的統計基礎上做懲罰。

配分判別函式的定義如下：

$P(Y|X)=\frac{e^{-\beta}E(Y,X)}{\int_{y\in Y}e^{-\beta}E(y,X)}$

其中$\beta$為係數，扔掉之後就是Softmax函式。

SoftmaxLoss

$NLL = - \sum _{i}^{examples}\sum _{k}^{classes}l(y(i)=k)\cdot log[Softmax(X_{k}^{i})]$

不做過多介紹，見我的早期博文：Softmax迴歸

前向傳播求Loss的時候只要記住一點區別：

I、在Logistic迴歸中，對每個樣本，Loss-=$\log(1-Sigmoid)$或者Loss-=$\log(Sigmoid)$

II、在Softmax迴歸中，對每個樣本，Loss只減去對應Label的$\log(Softmax)$

比較I、II也可以看出來，Logistic迴歸的二選一隻是Softmax迴歸的N選一的特例。

泛型Softmax求導

儘管DeepLearning的基石是多樣本與平行計算，但是在泛型章節中不考慮多樣本情況。

求導描述將盡量與Caffe框架中的命名方式同步，以便於理解程式碼。

同時假定Softmax Axis上，命中Label的下標為k。

SoftmaxLoss

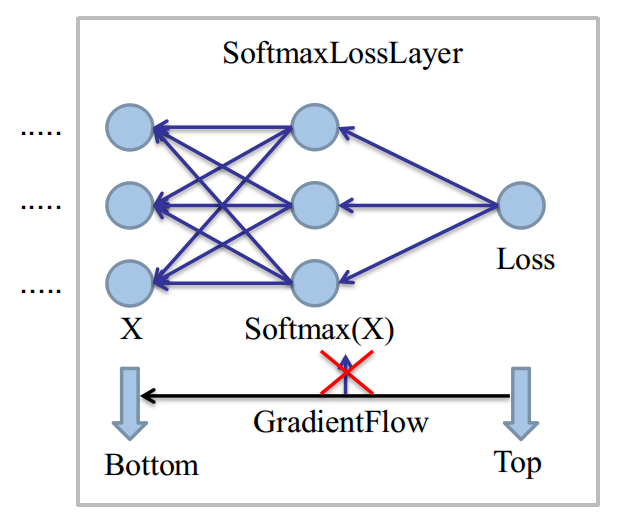
上圖是在當單樣本情況下，直接取Softmax Axis而畫的，現在我們假設這是一個N=3的分類問題。(0,1,2)

同時取Class=2作為當前樣本，命中的Label，即k=2。

由於Loss只和命中的分類有關，有：

$Softmax(X_{k})=\frac{e^{X_{k}}}{\sum _{i}e^{X_{i}}}$

則NLL (Negative-Log-Likelihood)為：

$NLL=-\log(Softmax(X_{k}))=-\log(\frac{e^{X_{K}}}{\sum _{i}e^{X_{i}}})\\ \quad \\ \qquad \qquad \qquad \qquad \qquad \qquad \; \; \,=\log(\sum _{i}e^{X_{i}})-log(e^{X_{k}}) \\  \quad \\ \qquad \qquad \qquad \qquad \qquad \qquad \; \; \, =\log(\sum _{i}e^{X_{i}})-X_{k}$

此時對於神經元$X_{k}$，有如下兩種求導方案：

I、  $BottomDiff(k)=\frac{\partial NLL}{\partial Softmax(X_{k})}\frac{\partial Softmax(X_{k})}{\partial X_{k}}$

II、 $BottomDiff(k)=\frac{\partial NLL}{\partial X_{k}}$

其中，第一種是沒有必要的，一般而言，Softmax的中間導數幾乎不會用到。

除非我們讓Softmax後面不接Loss，接其它的層，下一節會講這種特殊情況，求導相當複雜。

現在考慮更一般的神經元$X_{i}$，對NLL求導：

$\frac{\partial \log(\sum _{i}e^{X_{i}})-X_{k}}{\partial X_{i}}=\left\{\begin{matrix}\frac{e^{X_{K}}}{\sum _{i}e^{X_{i}}} - 1 \quad (i\neq k) \\ \\\frac{e^{X_{K}}}{\sum _{i}e^{X_{i}}} \quad (i=k)\\ \\0 \quad (if \;ignore\;i)\end{matrix}\right.$

程式設計時：

對於①條件：先Copy一下Softmax的結果(即prob_data)到bottom_diff，再對k位置的unit減去1

對於②條件：直接Copy一下Softmax的結果(即prob_data)到bottom_diff

對於③條件：找到ignore位置的unit，強行置為0。

圖示如下：

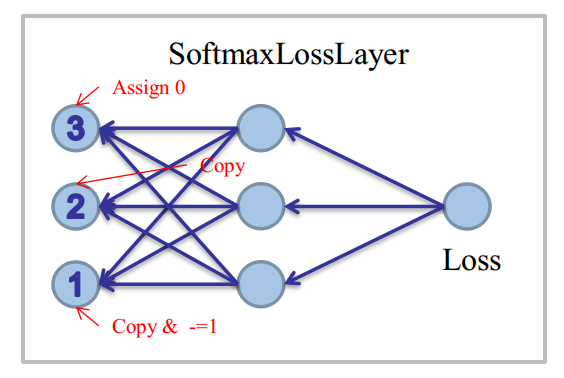
Softmax

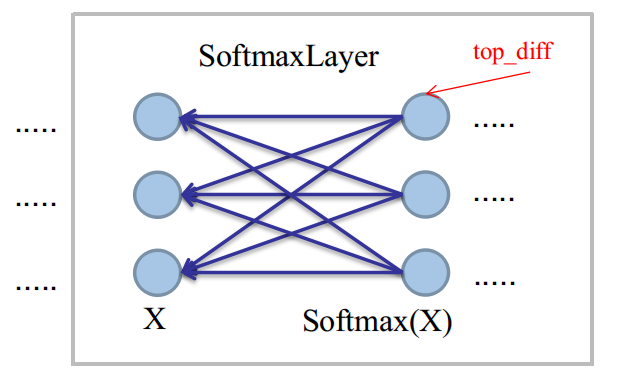
在SoftmaxLayer中，我們將會遇到最普遍的反向傳播任務：已知top_diff，求bottom_diff。

為了表述方便，設已知的top_diff的偏導表示式為：$\frac{\partial l}{Softmax(X)}$，則：

$BottomDiff(i)=\sum _{j}\frac{\partial l}{\partial Softmax(X_{j})}\frac{\partial Softmax(X_{j})}{\partial X_{i}}$

這是單獨對Softmax求導的最麻煩之處，由於全連線性，輸入神經元$X_{i}$將被全部的輸出神經元汙染。

更一般的，我們將其寫成：

$BottomDiff(i)=\frac{\partial l}{\partial Softmax(X)}\frac{\partial Softmax(X)}{\partial X_{i}}$。

考慮$\frac{\partial Softmax(X_{j})}{\partial X_{i}}$，有：

$\frac{\partial Softmax(X_{j})}{\partial X_{i}}=\left\{\begin{matrix}-Softmax(X_{j})*Softmax(X_{i})+Softmax(X_{i}) \quad i=j\\ \\ -Softmax(X_{j})*Softmax(X_{i}) \quad i\neq j\end{matrix}\right.$

聯合兩部分後，有：

$\sum \left\{\begin{matrix}-Softmax(X_{j})*\frac{\partial l}{\partial Softmax(X_{j})}*Softmax(X_{i})+Softmax(X_{i})*\frac{\partial l}{\partial Softmax(X_{j})} \quad i=j\\ \\ -Softmax(X_{j})*\frac{\partial l}{\partial Softmax(X_{j})}*Softmax(X_{i}) \quad i\neq j\end{matrix}\right.$

提取公共項部分：

$BottomDiff(i)=Softmax(X_{i})\left \langle  \sum {j}\left  \{-Softmax(X_{j})*\frac{\partial l}{\partial Softmax(X_{j})}\right \}+\frac{\partial l}{\partial Softmax(X_{i}) })\right \rangle\\ \quad \\  \qquad \qquad \qquad \; \; \; =TopData(i)\left \langle - \sum {j}\left  \{TopData(j)*TopDiff(j)\right \}+TopDiff(i) \right \rangle\\ \quad \\ \qquad \qquad \qquad \; \; \; =TopData(i)\left \langle - \left \{TopData \bullet  TopDiff \right \} +TopDiff(i) \right \rangle$

Caffe中做了以下兩點額外的優化：

I、由於對所有$X_{i}$，都要計算相同的點積項$\sum {j}\left  \{TopData(j)*TopDiff(j)\right \}$，

一個簡單優化是用GEMM做一次矩陣廣播，這樣，對每個樣本的Softmax Axis軸上的多個單元，只需點積一次。

II、由於top_data與bottom_diff的shape相同，最外層top_data可基於全樣本來乘，這在CUDA環境中，可以有效提升瞬時並行度。

空間Softmax求導

Fully Convolutional Networks for Semantic Segmentation

Caffe中將二軸Softmax(Batchsize/Softmax)擴充套件到了nD軸Softmax，用於全卷積網路。

這部分程式碼由此paper兩位作者Jonathan Long&Evan Shelhamer加入，Github的History如下：

空間Soffmax是為了Dense Pixel Prediction(密集點預測)而生的，對於一張300x500的輸入影象，

一次Softmax將產生300*500=15W個Loss，這屬於神經網路——畫素級理解，是目前最難的CV任務。

空間Softmax取消了Softmax前的InnerProduct做的Flatten，因為必須保證空間軸資訊。

一個語義分割的圖示如下：

GroundTruth、Outer_Num、Inner_Num

傳統機器學習中的樣本單數值Label，在ComputerVision中擴充套件為多數值Label後，即變成GroundTruth。

Caffe中採用以下格式來規範儲存與讀取：

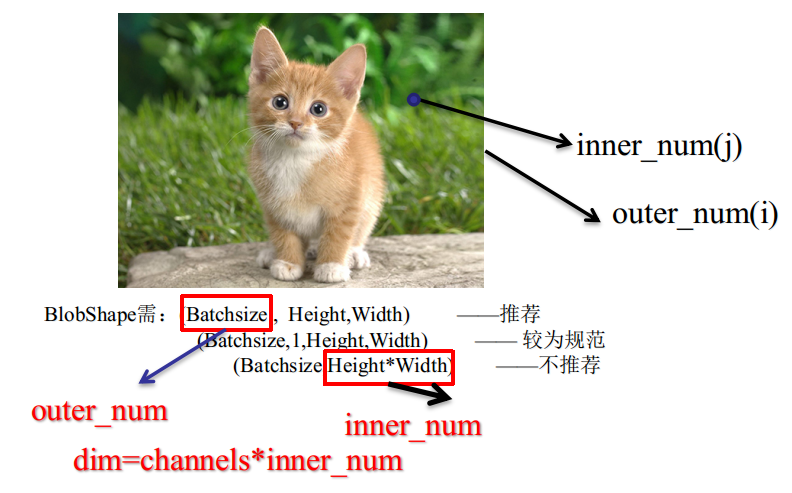
對於GroundTruth的$outer:inner=(i,j)$位置，即第$i$個樣本，空間$j$位置的Label，對應的Softmax向量如下：

$PixelExample=\left\{\begin{matrix}BottomData/BottomDiff(i*dim+0*inner+j) \quad class=0 \\
\quad \\ BottomData/BottomDiff(i*dim+1*inner+j) \quad class=1\\ \\ BottomData/BottomDiff(i*dim+2*inner+j) \quad class=2\\ \\...... \\ \\ BottomData/BottomDiff(i*dim+c*inner+j) \quad class=c\end{matrix}\right.$

這樣，對於outer_num數量的輸入影象，就變成了outer_num*inner_num個畫素樣本。

值得注意的是，目前最新的研究表明，在畫素級的理解中，batch_size大於1是沒有意義的，會嚴重減慢收斂速度。

輸入單張影象時，SGD做密集點預測，不會導致偏離最終的區域性最值點，因為15W的Loss近似可以看成batch_size=15,0000

空間Softmax(without GroundTruth)

從上節可知，空間軸(e.g. Height/Width)的引入，可看成是倍化了batch_size軸。

故在SoftmaxLayer中，對單樣本影象的輸入，需要多引入一次迴圈模擬多樣本，迴圈量即inner_num。

對於泛型Softmax中的點積運算，由計算單點積值，需要變化至求一組$TopData \bullet  TopDiff$：

同樣設$outer:inner=(i,j)$，那麼$j$位置的兩組點積向量分別如下：

$\bullet \left\{\begin{matrix}TopData/TopDiff(i*dim+0*inner+j) \quad class=0\\ \\ .........\\ \\ TopData/TopDiff(i*dim+c*inner+j) \quad class=c\\ \end{matrix}\right.$

由於點積的元素每次都要跳躍inner_num個位置，可利用BLAS庫做StridedDot運算，點積增量設為inner_num即可。

I、在GEMM矩陣廣播優化中，原來只需要將單點積值廣播成[classes,1]的矩陣，順次在Softmax-Axis軸上減去，即：

從$TopDiff(i*dim)$的一段減去，由於無空間軸時，dim=classes，TopDiff的shape為[batch_size,classes]，

矩陣的值恰好填充到下一樣本的開頭。

擴充套件空間軸時，則需要減去[classes,inner_num]個值，注意由於此時的shape為[batch_size,classes,inner_num]，

如果你要線性覆蓋，則需要先覆蓋class=0的inner_num個值，所以一定要保證廣播矩陣的shape為[classes,inner_num]。

然後再做一次向量減法。由於BLAS的GEMM運算支援$C=\beta C+\alpha AB $，可一步完成。

II、在最外圍的top_data乘算中，由於top_data與bottom_diff的shape相同，擴充套件空間軸無需調整程式碼。