關於卡方檢驗，下面這篇blog介紹的比較詳細，仔細思索之後，對一些點做如下說明，個人理解：
1. 關於假設“詞t與類別c無關”。這個假設應該變更為“詞t不是對分類有區分度的特徵”，（c是一個類別，除了c之外的所有資料組成另一個類別，類似邏輯迴歸多分類的方法）。一個詞的卡方檢驗值高，並不能說明詞一定與t強相關，只是說明詞t是兩個類別區分度較強的詞。這個和資訊增益的特徵選擇方法類似。
2. 如何判斷“詞與類別c相關”，嚴格來說，詞t在類別c中的類似詞頻的東東(比如tfidf)越高，詞t是類別c的特徵詞的可能行越大。可以通過簡單的tfidf來判斷。但是實踐來看，即使不通過tfidf來過濾，選出來的特徵也基本是positive特徵（詞t是類別c的強特徵），而不是negative特徵（參看1999年那篇文字分類特徵選擇的論文），尚未找到理論的證明。

http://www.blogjava.net/zhenandaci/archive/2008/08/31/225966.html

前文提到過，除了分類演算法以外，為分類文字作處理的特徵提取演算法也對最終效果有巨大影響，而特徵提取演算法又分為特徵選擇和特徵抽取兩大類，其中特徵選擇演算法有互資訊，文件頻率，資訊增益，開方檢驗

等等十數種，這次先介紹特徵選擇演算法中效果比較好的開方檢驗方法。

大家應該還記得，開方檢驗其實是數理統計中一種常用的檢驗兩個變數獨立性的方法。（什麼？你是文史類專業的學生，沒有學過數理統計？那你做什麼文字分類？在這搗什麼亂？）

開方檢驗最基本的思想就是通過觀察實際值與理論值的偏差來確定理論的正確與否。具體做的時候常常先假設兩個變數確實是獨立的（行話就叫做“原假設”），然後觀察實際值（也可以叫做觀察值）與理論值（這個理論值是指“如果兩者確實獨立”的情況下應該有的值）的偏差程度，如果偏差足夠小，我們就認為誤差是很自然的樣本誤差，是測量手段不夠精確導致或者偶然發生的，兩者確確實實是獨立的，此時就接受原假設；如果偏差大到一定程度，使得這樣的誤差不太可能是偶然產生或者測量不精確所致，我們就認為兩者實際上是相關的，即否定原假設，而接受備擇假設

。

那麼用什麼來衡量偏差程度呢？假設理論值為E（這也是數學期望的符號哦），實際值為x，如果僅僅使用所有樣本的觀察值與理論值的差值x-E之和

來衡量，單個的觀察值還好說，當有多個觀察值x₁，x₂，x₃的時候，很可能x₁-E，x₂-E，x₃-E的值有正有負，因而互相抵消，使得最終的結果看上好像偏差為0，但實際上每個都有偏差，而且都還不小！此時很直接的想法便是使用方差代替均值，這樣就解決了正負抵消的問題，即使用

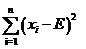
這時又引來了新的問題，對於500的均值來說，相差5其實是很小的（相差1%），而對20的均值來說，5相當於25%的差異，這是使用方差也無法體現的。因此應該考慮改進上面的式子，讓均值的大小不影響我們對差異程度的判斷

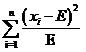                            式（1）

上面這個式子已經相當好了。實際上這個式子就是開方檢驗使用的差值衡量公式。當提供了數個樣本的觀察值x₁，x₂，……x_i，……x_n之後，代入到式（1）中就可以求得開方值，用這個值與事先設定的閾值比較，如果大於閾值（即偏差很大），就認為原假設不成立，反之則認為原假設成立。

在文字分類問題的特徵選擇階段，我們主要關心一個詞t（一個隨機變數）與一個類別c（另一個隨機變數）之間是否相互獨立？如果獨立，就可以說詞t對類別c完全沒有表徵作用，即我們根本無法根據t出現與否來判斷一篇文件是否屬於c這個分類。但與最普通的開方檢驗不同，我們不需要設定閾值，因為很難說詞t和類別c關聯到什麼程度才算是有表徵作用，我們只想借用這個方法來選出一些最最相關的即可。

此時我們仍然需要明白對特徵選擇來說原假設是什麼，因為計算出的開方值越大，說明對原假設的偏離越大，我們越傾向於認為原假設的反面情況是正確的。我們能不能把原假設定為“詞t與類別c相關“？原則上說當然可以，這也是一個健全的民主主義社會賦予每個公民的權利（笑），但此時你會發現根本不知道此時的理論值該是多少！你會把自己繞進死衚衕。所以我們一般都使用”詞t與類別c不相關“來做原假設。選擇的過程也變成了為每個詞計算它與類別c的開方值，從大到小排個序（此時開方值越大越相關），取前k個就可以（k值可以根據自己的需要選，這也是一個健全的民主主義社會賦予每個公民的權利）。

好，原理有了，該來個例子說說到底怎麼算了。

比如說現在有N篇文件，其中有M篇是關於體育的，我們想考察一個詞“籃球”與類別“體育”之間的相關性（任誰都看得出來兩者很相關，但很遺憾，我們是智慧生物，計算機不是，它一點也看不出來，想讓它認識到這一點，只能讓它算算看）。我們有四個觀察值可以使用：

1.包含“籃球”且屬於“體育”類別的文件數，命名為A

2.包含“籃球”但不屬於“體育”類別的文件數，命名為B

3.不包含“籃球”但卻屬於“體育”類別的文件數，命名為C

4.既不包含“籃球”也不屬於“體育”類別的文件數，命名為D

用下面的表格更清晰：

特徵選擇	1．屬於“體育”	2．不屬於“體育”	總計
1．包含“籃球”	A	B	A+B
2．不包含“籃球”	C	D	C+D
總數	A+C	B+D	N

如果有些特點你沒看出來，那我說一說，首先，A+B+C+D=N（這，這不廢話嘛）。其次，A+C的意思其實就是說“屬於體育類的文章數量”，因此，它就等於M，同時，B+D就等於N-M。

好，那麼理論值是什麼呢？以包含“籃球”且屬於“體育”類別的文件數為例。如果原假設是成立的，即“籃球”和體育類文章沒什麼關聯性，那麼在所有的文章中，“籃球”這個詞都應該是等概率出現，而不管文章是不是體育類的。這個概率具體是多少，我們並不知道，但他應該體現在觀察結果中（就好比拋硬幣的概率是二分之一，可以通過觀察多次拋的結果來大致確定），因此我們可以說這個概率接近

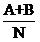
（因為A+B是包含“籃球”的文章數，除以總文件數就是“籃球”出現的概率，當然，這裡認為在一篇文章中出現即可，而不管出現了幾次）而屬於體育類的文章數為A+C，在這些個文件中，應該有

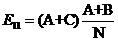
篇包含“籃球”這個詞（數量乘以概率嘛）。

但實際有多少呢？考考你（讀者：切，當然是A啦，表格裡寫著嘛……）。

此時對這種情況的差值就得出了（套用式（1）的公式），應該是

同樣，我們還可以計算剩下三種情況的差值D₁₂，D₂₁，D₂₂，聰明的讀者一定能自己算出來（讀者：切，明明是自己懶得寫了……）。有了所有觀察值的差值，就可以計算“籃球”與“體育”類文章的開方值

把D₁₁，D₁₂，D₂₁，D₂₂的值分別代入並化簡，可以得到

詞t與類別c的開方值更一般的形式可以寫成

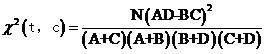           式（2）

接下來我們就可以計算其他詞如“排球”，“產品”，“銀行”等等與體育類別的開方值，然後根據大小來排序，選擇我們需要的最大的數個詞彙作為特徵項就可以了。

實際上式（2）還可以進一步化簡，注意如果給定了一個文件集合（例如我們的訓練集）和一個類別，則N，M，N-M（即A+C和B+D）對同一類別文件中的所有詞來說都是一樣的，而我們只關心一堆詞對某個類別的開方值的大小順序，而並不關心具體的值，因此把它們從式（2）中去掉是完全可以的，故實際計算的時候我們都使用

            式（3）

好啦，並不高深對不對？

針對英文純文字的實驗結果表明：作為特徵選擇方法時，開方檢驗和資訊增益的效果最佳（相同的分類演算法，使用不同的特徵選擇演算法來得到比較結果）；文件頻率方法的效能同前兩者大體相當，術語強度方法效能一般；互資訊方法的效能最差（文獻[17]）。

但開方檢驗也並非就十全十美了。回頭想想A和B的值是怎麼得出來的，它統計文件中是否出現詞t，卻不管t在該文件中出現了幾次，這會使得他對低頻詞有所偏袒（因為它誇大了低頻詞的作用）。甚至會出現有些情況，一個詞在一類文章的每篇文件中都只出現了一次，其開方值卻大過了在該類文章99%的文件中出現了10次的詞，其實後面的詞才是更具代表性的，但只因為它出現的文件數比前面的詞少了“1”，特徵選擇的時候就可能篩掉後面的詞而保留了前者。這就是開方檢驗著名的“低頻詞缺陷“。因此開方檢驗也經常同其他因素如詞頻綜合考慮來揚長避短。

好啦，關於開方檢驗先說這麼多，有機會還將介紹其他的特徵選擇演算法。

附：給精通統計學的同學多說幾句，式（1）實際上是對連續型的隨機變數的差值計算公式，而我們這裡統計的“文件數量“顯然是離散的數值（全是整數），因此真正在統計學中計算的時候，是有修正過程的，但這種修正仍然是隻影響具體的開方值，而不影響大小的順序，故文字分類中不做這種修正。