LeetCode - 221. Maximal Square(求最大的全是1的正方形)

• 暴力 (O(N^5))
• 改進動態規劃(O(N^３))
• 優化動態規劃(O(N^2))

題目連結

題目

暴力 (O(N^5))

暴力O(N) * O(M) * O(min(N ， M)) * O(N) * O(M)，也就是O(N^5)，但是也能通過…

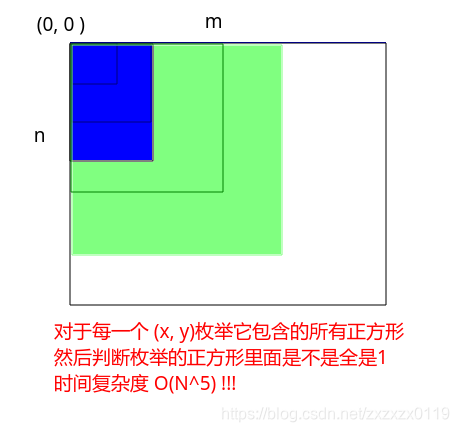
• 列舉0 ~ n和0 ~ m，然後列舉這個範圍內的所有正方形。這裡時間複雜度為O(N) * O(M) * O(min(N, M))；
• 然後列舉的每一個正方形還需要判斷這個正方形內是不是全都是1
  ，時間複雜度O(N * M )；

class Solution {
    public int maximalSquare(char[][] matrix) {
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0)
            return 0;
        int n = matrix.length;
        int m = matrix[0].length;
        int res = 0;
        for(int x = 0; x < n; x++
 
){      // 列舉左上角的 x
            for(int y = 0; y < m; y++){  // 列舉左上角的 y
                for(int size = Math.min(n-x, m-y); size >= 1; size--){ // 列舉 [1, min(n-x, m-y)]這麼多的方陣(size表示方陣大小)
                    if(check(matrix, x, y, size)){  //檢查這個方陣是否全為1
                        res = Math.max(res, size*size)
 
;
                        break;  //因為size是從大->小，所以可以break
                    }
                }
            }
        }
        return res;
    }
    
    private boolean check(char[][] matrix, int x, int y, int size){
        for(int i = x; i < x+size; i++){
            for(int j = y; j < y+size; j++){
                if(matrix[i][j] - '0' == 0)
                    return false;
            }
        }
        return true;
    }
}

改進動態規劃(O(N^３))

上面的check()函式在判斷大正方形的時候其實包含了很多的子問題。

可以通過改進上面方式中的 check()過程來優化複雜度:

• 將 check()提前預處理好，這個過程需要用到動態規劃；
• 這個動態規劃用到一個二維sums陣列，sum[x][y] (或者sums[i][j]) 代表的是 (0, 0) ~ (x, y)這個矩陣的和；

看下圖對於sum( 0~x, 0~y )的求法:

其中兩個藍色部分有一個重疊的綠色部分，所以要多減去一個。

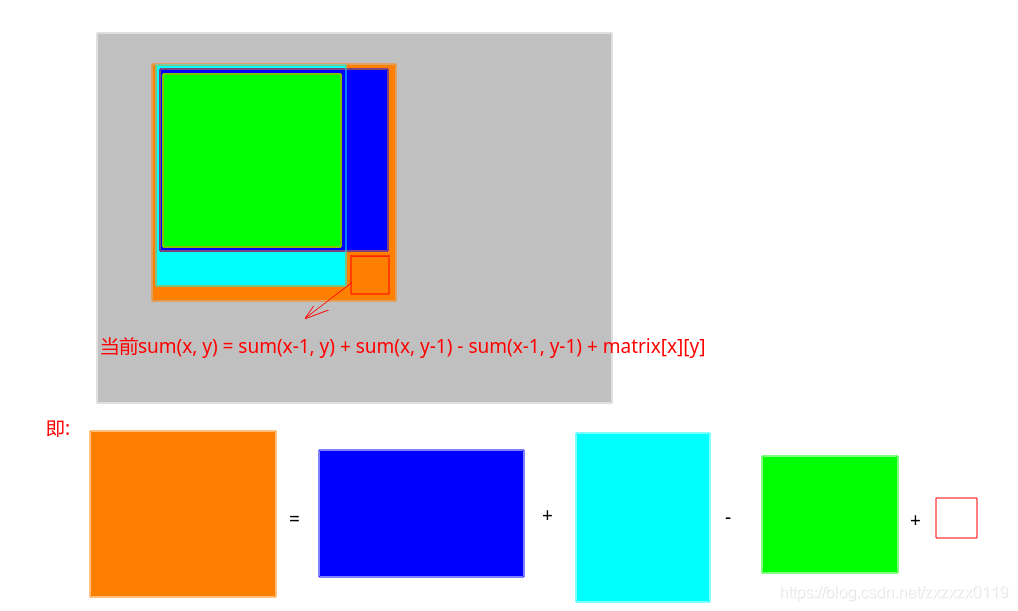
如果求出了上面的sums陣列，我們就可以在O(1)時間內檢查這個列舉的正方形是不是全都是1了，我們只需要求列舉的正方形的和是不是等於size * size就可以判斷。

怎麼由當前已經求得的sums陣列得到當前列舉的正方形的和呢?

可以由sum陣列得到當前以(x, y)為左上角頂點的正方形的和，大體框架如下:

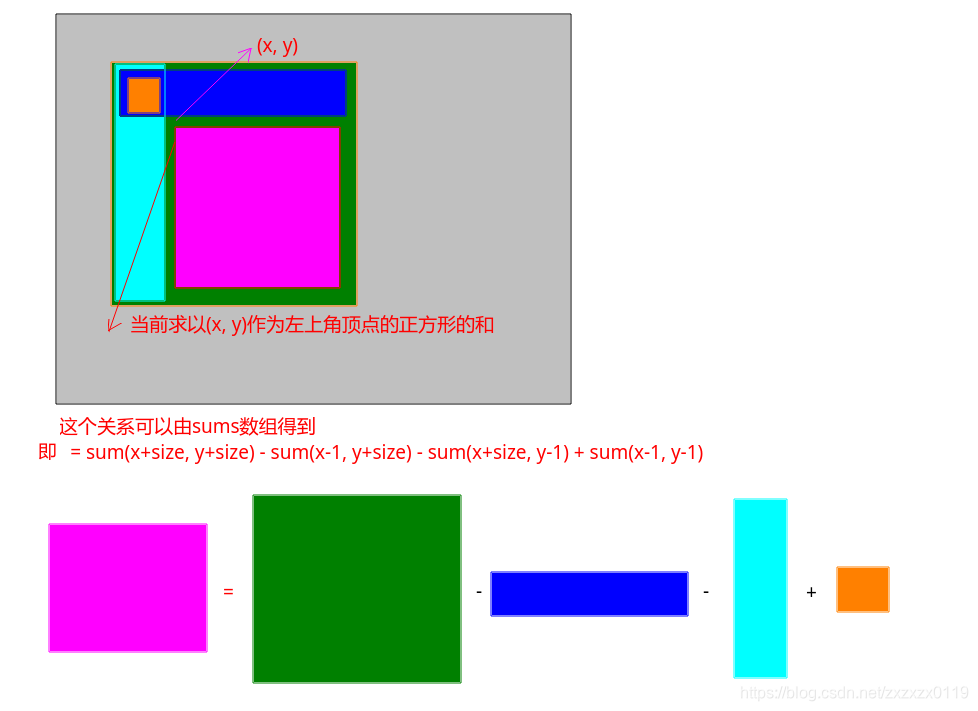
不過這裡要注意程式碼的處理:

我們sums陣列起始從1, 1開始會比較方便處理，所以實際上下面的程式碼中sums[x, y]表示的是[0 ~ i-1, 0 ~ j-1]內的和。不然判斷邊界就會比較麻煩，所以檢查的時候第三層迴圈size = Math.min(n-x+1, m-y+1)開始也需要注意。

class Solution {
    public int maximalSquare(char[][] matrix) {
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0)
            return 0;
        int n = matrix.length;
        int m = matrix[0].length;
        //預處理出 (0, 0) ~ (x,y) 矩陣的裡面的數的和
        int[][] sums = new int[n+1][m+1];
        for(int x = 1; x <= n; x++){ // 從[0,0]到[x,y]遞推
            for(int y = 1; y <= m; y++){
                sums[x][y] = sums[x][y-1] + sums[x-1][y] - sums[x-1][y-1] + matrix[x-1][y-1]-'0';
            }
        }
        int res = 0;
        for(int x = 1; x <= n; x++){      // 列舉左上角的 x
            for(int y = 1; y <= m; y++){  // 列舉左上角的 y
                for(int size = Math.min(n-x+1, m-y+1); size >= 1; size--){ // 列舉 [1, min(n-x, m-y)]這麼多的方陣(size表示方陣大小)
                    int sum = sums[x+size-1][y+size-1] - sums[x+size-1][y-1] - sums[x-1][y+size-1] + sums[x-1][y-1];
                    if(sum == size*size){
                        res = Math.max(res, size*size);
                        break;
                    }
                }
            }
        }
        return res;
    }
}

這裡LeetCode - 304. Range Sum Query 2D - Immutable 就完全是這種方法解決:

class NumMatrix {

    private int[][] sums;
    
    public NumMatrix(int[][] matrix) {
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0)
            return;
        int n = matrix.length, m = matrix[0].length;
        sums = new int[n+1][m+1];
         // sum[i, j]表示 矩形[0 ~ i-1, 0 ~ j-1]的數的和
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                sums[i+1][j+1] = sums[i+1][j] + sums[i][j+1] - sums[i][j] + matrix[i][j];
            }
        }
    }
    
    // [row1, col1] -> [row2, col2]
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return sums[row2+1][col2+1] - sums[row2+1][col1] - sums[row1][col2+1] + sums[row1][col1];
    }
}

其實sums[i, j]也可以表示是[0 ~ i, 0 ~j]矩陣的和，但是這樣下面的函式處理會不方便，所以我們用sums[i, j]表示的是
[0 ~ i-1, 0 ~ j-1]內的和。

下面是sums[i][j]表示[0 ~ i, 0 ~j]矩陣的和的程式碼:

public NumMatrix(int[][] matrix) {
    if(matrix == null || matrix.length == 0 || matrix[0].length == 0)
        return;
    int n = matrix.length, m = matrix[0].length;
    sums = new int[n+1][m+1]; // sum[i, j]表示 矩形[0~i, 0~j]的數的和

    sums[0][0] = matrix[0][0];
    for(int i = 1; i < n; i++)
        sums[i][0] = sums[i-1][0] + matrix[i][0];
    for(int j = 1; j < m; j++)
        sums[0][j] = sums[0][j-1] + matrix[0][j];
    for(int i = 1; i < n; i++){
        for(int j = 1; j < m; j++){
            sums[i][j] = sums[i-1][j] + sums[i][j-1] - sums[i-1][j-1] + matrix[i][j];
        }
    }
}

優化動態規劃(O(N^2))

這個方法是本題的最優解。

其中dp[i][j]表示的是從(0, 0)到當前 (x, y)能構成的最大的正方形的size(邊的大小)。

則:

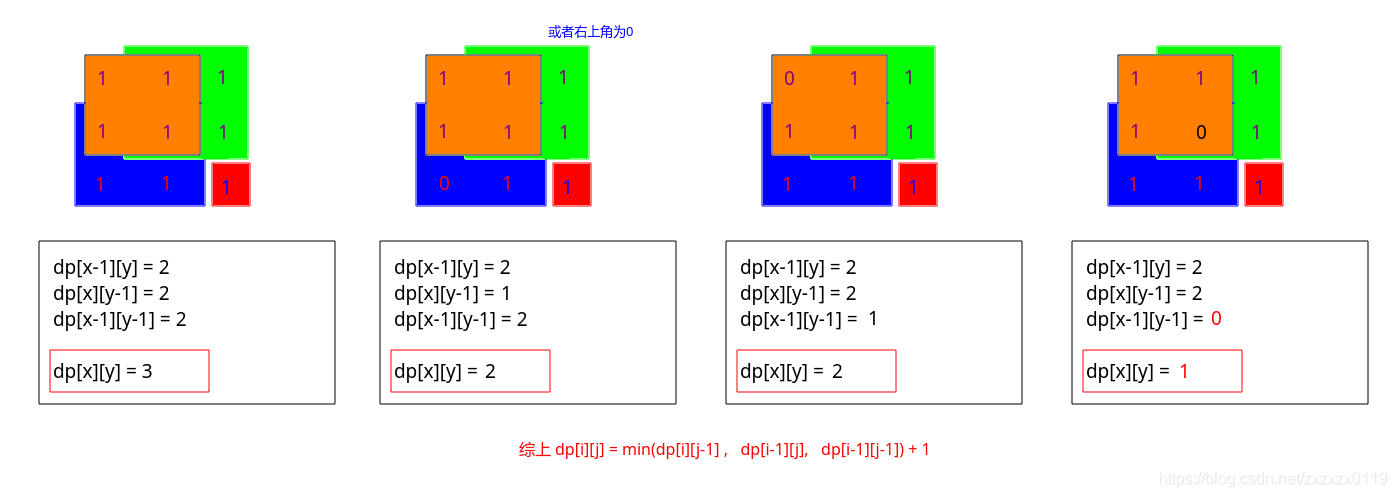
• 如果當前matrix[i][j] == 0，則dp[i][j] = 0；
• 其他一般的情況，看下圖，可以得到dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) + 1；

class Solution {
    public int maximalSquare(char[][] matrix) {
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0)
            return 0;
        int n = matrix.length;
        int m = matrix[0].length;
        
        int[][] dp = new int[n][m];
        
        int res = 0;
        for(int i = 0; i < n; i++){
            dp[i][0] = matrix[i][0] - '0';
            res = Math.max(res, dp[i][0]);
        }
        for(int j = 0; j < m; j++){
            dp[0][j] = matrix[0][j] - '0';
            res = Math.max(res, dp[0][j]);
        }
        for(int i = 1; i < n; i++){
            for(int j = 1; j < m; j++){
                if(matrix[i][j] - '0' == 0)
                    continue;
                dp[i][j] = 1 + Math.min(dp[i][j-1], Math.min(dp[i-1][j], dp[i-1][j-1]));
                res = Math.max(res, dp[i][j]);
            }
        }
        return res * res;
    }
}