圖的儲存結構與搜尋
- 圖是什麼
圖,顧名思義,就是一張大大的網,網中的每個節點都與另外一個節點直接或者間接的聯絡。網際網路就是一個大大的圖,從A到B到C經過的路由,就是圖的搜尋演算法。
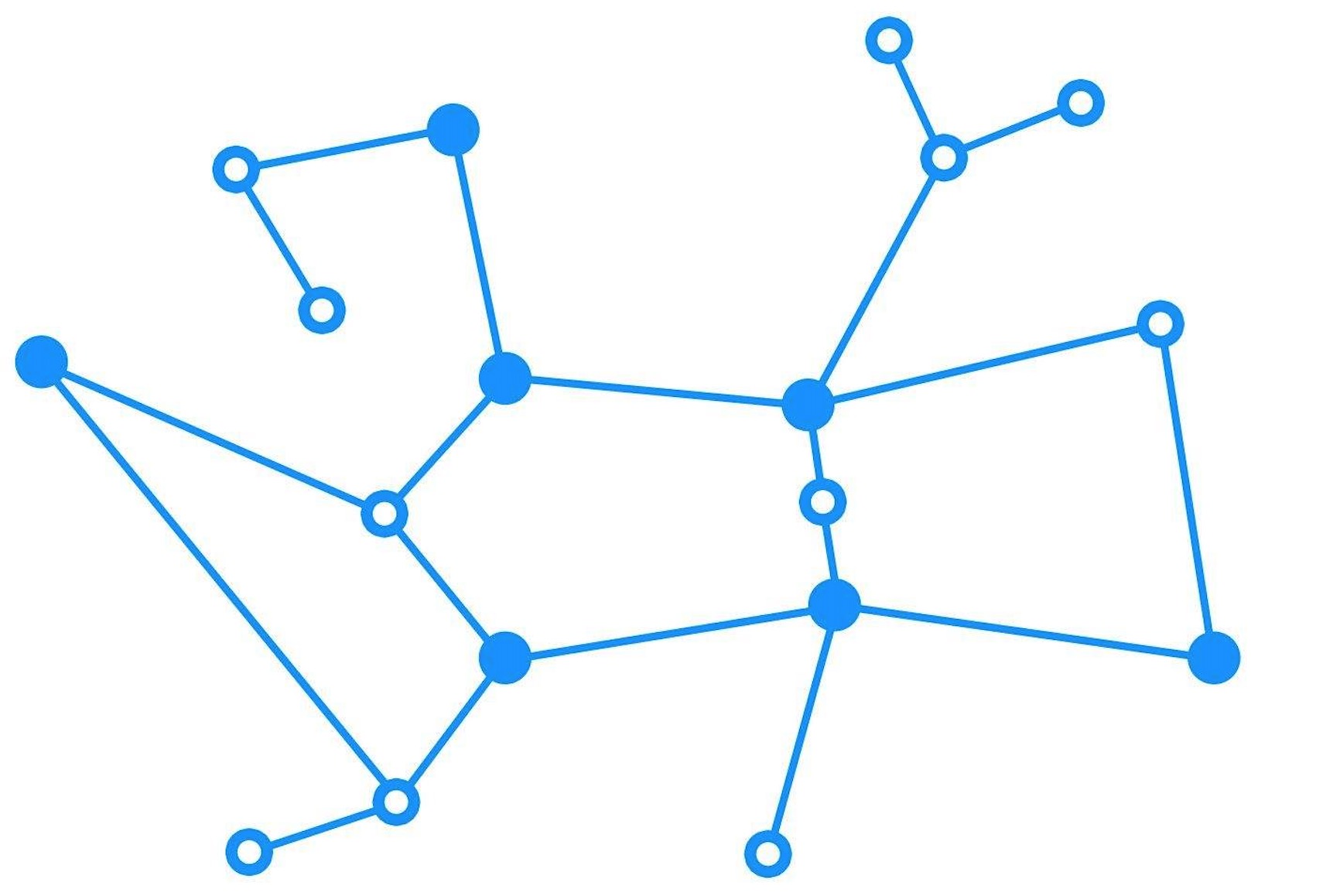
要給圖下一個定義,那就是在眾多離散節點中可以產生迴路的資料結構。比之線性資料結構的單線特性,樹形結構的多路分叉特性,圖的最大特點就是有迴路的樹形結構。圖可以表示很多具體的事物,它是現實的一種抽象模型。比如地圖定址、路由定址、狀態機等。圖是用來當做計算模型使用的,在某些高階場合十分適用。
- 圖的定義
圖的定義主要通過兩種方式:1.鄰接矩陣;2.鄰接表。
還有一種非常複雜的定義:十字連結串列。
鄰接矩陣的定義十分的直觀,它通過二維矩陣來表示節點之間的消耗。比如a[i][j]表示從i節點到j節點的消耗,可以定義為0則沒有通路。 在無向圖中,通常這個矩陣是對稱陣,即a[i][j] = a[j][i];在有向圖中,它是反對稱陣,即a[i][j] = -a[j][i]。可以看到使用鄰接矩陣來儲存消耗了額外的一半空間,但是查詢非常的方便。
鄰接表,使用鄰接表來儲存圖,則儲存一個連結串列陣列,每個頭結點就是圖的節點,它指向與它有聯絡的節點並存儲消耗。這種方式節省了空間,但是查詢節點是否有聯絡的時候必須遍歷連結串列,這樣增加了時間的消耗。
圖的種類大概會有:無向圖,有向圖,雙向圖。
Java的鄰接矩陣實現,用一個類儲存矩陣,在建構函式時候傳入大小,新建的是n*n的矩陣,然後就是寫API了,無外乎CRUD。

package Graph; import java.util.ArrayList; import java.util.List; /** * 鄰接矩陣 * @author ctk * */ publicclass AdjacencyMatrixGraph { private int edges ; private int[][] weight; private List<String> nodes; private int vertex; public AdjacencyMatrixGraph(int vertex){ this.vertex = vertex; weight = new int[vertex][vertex]; nodes = new ArrayList<>(vertex); edges= 0; } //獲得節點數 public int getNodes(){ return nodes.size(); } //獲得邊數 public int getEdges(){ return edges; } //插入節點 public boolean insertNode(String name){ if(nodes.size() == vertex) return false; nodes.add(name); return true; } //設定權重 public boolean setWeight(int i,int j,int weight){ if(i >= vertex || j >= vertex || i < 0 || j < 0) return false; if(this.weight[i][j] == 0) edges++; this.weight[i][j] = weight; return true; } //獲得i節點 public String getNode(int i){ if(i > nodes.size()) return null; else return nodes.get(i); } //獲得邊權重 public int getWeight(int i,int j){ if(i >= vertex || j >= vertex || i < 0 || j < 0) return -1; else return weight[i][j]; } //刪除邊 public void deleteEdge(int i,int j){ if(i >= vertex || j >= vertex || i < 0 || j < 0){ System.out.println("越界"); return ; } weight[i][j] = 0; } //列印矩陣 public void printMatrix(){ for(int i=0;i<weight.length;i++) { for(int j=0;j<weight[i].length;j++){ System.out.print(weight[i][j]+" "); } System.out.println(); } } public static void main(String[] args) { AdjacencyMatrixGraph graph = new AdjacencyMatrixGraph(5); String node1 = "n1"; String node2 = "n2"; String node3 = "n3"; String node4 = "n4"; graph.insertNode(node1); graph.insertNode(node2); graph.insertNode(node3); graph.insertNode(node4); graph.setWeight(0, 1, 2); graph.setWeight(0, 2, 5); graph.setWeight(2, 3, 8); graph.setWeight(3, 0, 7); System.out.println("邊數:"+graph.getEdges()); System.out.println("節點數:"+graph.getNodes()); graph.printMatrix(); } }

鄰接表的實現,寫一個節點類,然後初始化的時候新建這麼大的陣列,把每個空格放入新建的節點。

package Graph; import java.util.ArrayList; import java.util.List; /** * 鄰接表實現的圖 * @author ctk * */ public class ListGraph { private List<GraphNode> gNodes ; private int vertex ; private int edges ; public ListGraph(int vertex){ this.vertex = vertex ; gNodes = new ArrayList<>(vertex); for(int i=0;i<vertex;i++) { GraphNode gnode = new GraphNode(); gnode.setNodeIndex(i); gnode.setNext(null); gNodes.add(gnode); } } //新增邊 public void addEdge(int i,int j,int weight){ if(i >= vertex || j >= vertex || i < 0 || j < 0) { System.out.println("輸入的i和j超過範圍"); return; } GraphNode gnode = gNodes.get(i); boolean isAlter = false; while(gnode.getNext() != null) { if(gnode.getNodeIndex() == j) { gnode.setData(weight); isAlter = true; break; } gnode = gnode.getNext(); } if(i == j){ gnode.setData(weight); isAlter = true; } if(!isAlter){ GraphNode edgeNode = new GraphNode(); edgeNode.setData(weight); edgeNode.setNodeIndex(j); edgeNode.setNext(null); gnode.setNext(edgeNode); } } //生成鄰接矩陣 public int[][] getMartix(){ int[][] martix = new int[vertex][vertex]; GraphNode temp = null; for(int i=0;i<gNodes.size();i++){ temp = gNodes.get(i); while(temp != null){ martix[i][temp.getNodeIndex()] = temp.getData(); temp = temp.getNext(); } } return martix; } //獲得某邊 public int getEdge(int i,int j){ int weight = 0; if(i >= vertex || j >= vertex || i < 0 || j < 0) { System.out.println("輸入的i和j超過範圍"); return weight; } GraphNode temp = gNodes.get(i); while(temp != null){ if(temp.getNodeIndex() == j){ weight = temp.getData(); break; } temp = temp.getNext(); } return weight; } public int getVertex() { return vertex; } public int getEdges() { return edges; } public static void main(String[] args) { ListGraph graph = new ListGraph(5); graph.addEdge(0, 1, 2); graph.addEdge(0, 2, 3); graph.addEdge(1, 1, 4); graph.addEdge(2, 3, 6); int[][] martix = graph.getMartix(); for(int i =0;i<martix.length;i++){ for(int j=0;j<martix[i].length;j++) System.out.print(martix[i][j]+" "); System.out.println(); } System.out.println("獲取邊<1,1> :"+graph.getEdge(1, 1)); } } //節點類 class GraphNode{ private int nodeIndex; private int data; private GraphNode next; public int getNodeIndex() { return nodeIndex; } public void setNodeIndex(int nodeIndex) { this.nodeIndex = nodeIndex; } public int getData() { return data; } public void setData(int data) { this.data = data; } public GraphNode getNext() { return next; } public void setNext(GraphNode next) { this.next = next; } }

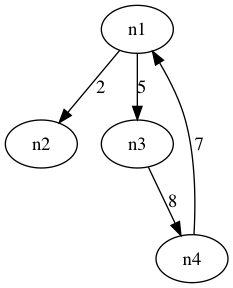
上圖使用一種工具Graphviz來實現畫圖的,有興趣的同學可以百度一下,有一個建模語言dot。
- 圖遍歷演算法
對線性或者樹形進行遍歷,通常都十分簡單,因為到null就停止了,而圖是有迴路的資料結構,如果使用之前的遍歷策略,則很容易就死迴圈了。
對於圖來說,遍歷的策略通常是:深度優先(DFS),廣度優先(BFS)。
深度優先(DFS)
對於一個節點來說,儘可能的往下走,走到盡頭再去選擇這個節點的另外一條路。
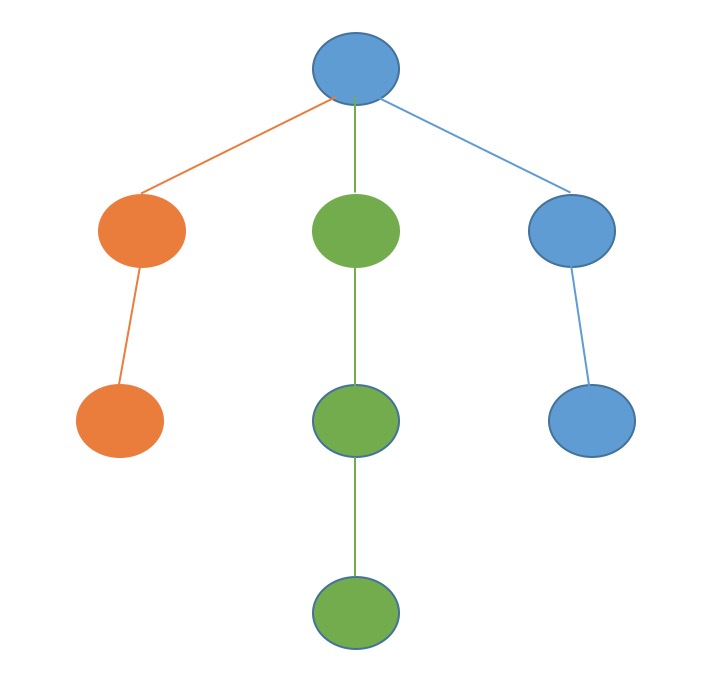
以上圖來說,從根節點觸發,先一個一個遍歷完橙色,再遍歷完綠色,最後遍歷完藍色。當然選擇節點的時候有個能先綠色,也可能先藍色,不過一旦選擇一種顏色之後就會遍歷到底。樹形結構明白之後,圖的DFS更加清楚了。
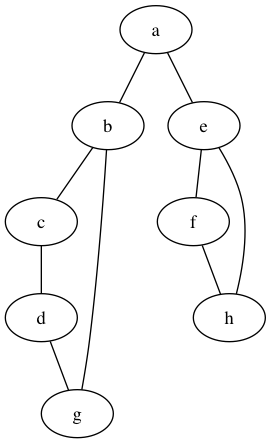
以上圖為例,從a節點出發的DFS,假設裝入都是按順序的,首先遍歷的是a-b-c-d-g,然後遍歷e-f-h。總之順序就是a-b-c-d-g-e-f-h。
要實現深度優先的搜尋,觀察這個遍歷順序,知道每次把節點拿到之後子節點優先遍歷,那是一個先進後出的順序,使用棧來儲存。比如a拿到之後他的子節點b,e入棧,假設b在棧頂,則彈出遍歷b後把b的子節點c,g壓入棧中。如此往復,直到所有的節點都Visited。
使用C++定義一個集合專門存放節點的。

const int MAX = 100; //圖節點 typedef struct { int edges[MAX][MAX]; int n; int e; int visited[MAX]; }MGraph;


這是鄰接矩陣的儲存方式。接著是深度優先遍歷方法。並採用上述例子模型。

void DFS2(MGraph &G,int v){ stack<int> temp; cout<<"節點:"<<v<<" "; G.visited[v] = 1; temp.push(v); while(!temp.empty()){ int i,j; i=temp.top(); for(j=0;j<G.n;j++){ if(G.edges[i][j] != 0 && G.visited[j] == 0) { cout<<"節點:"<<j<<" "; G.visited[j] = 1; temp.push(j); break; } } if(j==G.n) temp.pop(); } cout<<endl; }

由於深度優先是一個棧模型,所以遞迴很符合它的運算模型,所以可以使用遞迴來計算。

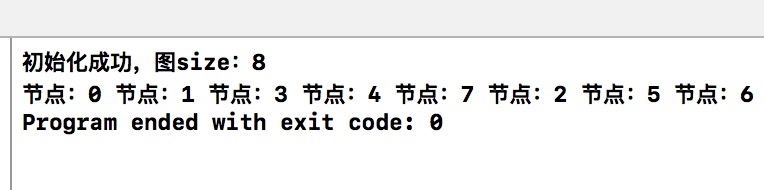
void DFS1(MGraph &G,int v){ int i; cout<<"節點:"<<v<<" "; G.visited[v] = 1; for(i=0;i<G.n;i++) { if(G.edges[v][i] !=0 && G.visited[i] == 0) { DFS1(G, i); } } }

程式的執行結果是。
廣度優先(BFS)
廣度優先顧名思義,類似於樹的層序遍歷。把這個節點的子節點全部遍歷之後,再把子節點的孩子遍歷。在戰爭中類似於把周圍的領土先佔領完畢再進行擴張。
由於廣度優先這個特性,使得它的實現是使用佇列這種先進先出的計算模式。把父節點進入佇列,然後出佇列的時候把父節點的孩子節點依次加入佇列尾部。
廣度優先的C++程式碼。

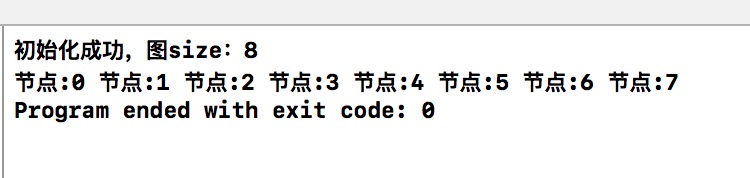
void BFS(MGraph &G,int v){ queue<int> Q; cout<<"節點:"<<v<<" "; Q.push(v); while(!Q.empty()){ int i,j; i=Q.front(); Q.pop(); for(j=0;j<G.n;j++){ if(G.edges[i][j] != 0 && G.visited[j] == 0){ cout<<"節點:"<<j<<" "; G.visited[j] = 1; Q.push(j); } } } cout<<endl; }

同上例,BFS的結果是。
從效能上來講,深度優先優於廣度優先,因為廣度優先的佇列會比棧容量要大,採用哪種搜尋主要看需求。
相關推薦
圖的儲存結構與搜尋
圖是什麼 圖,顧名思義,就是一張大大的網,網中的每個節點都與另外一個節點直接或者間接的聯絡。網際網路就是一個大大的圖,從A到B到C經過的路由,就是圖的搜尋演算法。 要給圖下一個定義,那就是在眾多離散節點中可以產生迴路的資料結構。比之線性資料結構的單線特性,樹形結構的多路分叉特性,圖的最大特點
演算法與資料結構(四) 圖的物理儲存結構與深搜、廣搜(Swift版)
開門見山,本篇部落格就介紹圖相關的東西。圖其實就是樹結構的升級版。上篇部落格我們聊了樹的一種,在後邊的部落格中我們還會介紹其他型別的樹,比如紅黑樹,B樹等等,以及這些樹結構的應用。本篇部落格我們就講圖的儲存結構以及圖的搜尋,這兩者算是圖結構的基礎。下篇部落格會在此基礎上聊一下最小生成樹的Prim演算法以及克魯
順序儲存結構與鏈式儲存結構的比較(也可以說的順序表與連結串列的比較)
1、鏈式儲存結構的儲存空間在邏輯上是連續的,但是在物理上是離散的;而順序儲存結構的儲存空間在邏輯上是連續的,在物理上也是連續的。 2、鏈式儲存儲存密度小,但空間利用率較高;順序儲存儲存密度大,但空間利用率較低。 3、順序結構優點是可以隨機讀取元素,缺點是插入和刪除元素要移動大量元素,
資料結構 筆記:樹的儲存結構與實現
樹的結點的儲存結構 GTreeNode的設計與實現 template<typename T> class GTreeNode : public TreeNode<T> { public: LinkList<GTreeeNode<T>*&
第八節課:第六章儲存結構與磁碟劃分
筆記 (借鑑請修改) 6.3、檔案系統與資料資料 目前linux最常見的檔案系統: ext3:日誌檔案系統。宕機時可自動恢復資料資料,容量越大恢復時間越長,且不能保證百分百不
資料結構專題——二叉樹的儲存結構與基本操作
一般來說,二叉樹使用連結串列來定義。 與普通連結串列的差別在於,二叉樹每個節點有兩條出邊,因此指標域變成了兩個,分別指向左子樹根節點地址和右子樹的根節點地址,如果某個子樹不存在,則指向NULL,其他地方與普通連結串列完全相同,這樣的連結串列又被叫作二叉連結串列。 二叉樹資
棧的順序儲存結構與基本運算
// // main.cpp // 棧的基本運算 // // Created by 柯木超 on 2018/12/3. // Copyright © 2018年 柯木超. All rights reserved. // #include <iostream> #define m
C++學習之deque底層儲存結構與迭代器失效情況
C++ STL容器deque和vector很類似,也是採用動態陣列來管理元素。 使用deque之前需包含標頭檔案: #include <deque> 它是定義在名稱空間std內的一個class template: template<class _
圖 | 儲存結構:鄰接表、鄰接多重表、十字連結串列及C語言實現
上一節介紹瞭如何使用順序儲存結構儲存圖,而在實際應用中最常用的是本節所介紹的鏈式儲存結構:圖中每個頂點作為連結串列中的結點,結點的構成分為資料域和指標域,資料域儲存圖中各頂點中儲存的資料,而指標域負責表示頂點之間的關聯。 使用鏈式儲存結構表示圖的常用方法有 3 種:鄰接表、
圖 | 儲存結構:鄰接矩陣及C語言實現
使用圖結構表示的資料元素之間雖然具有“多對多”的關係,但是同樣可以採用順序儲存,也就是使用陣列有效地儲存圖。 鄰接矩陣 鄰接矩陣(Adjacency Matrix),又稱 陣列表示法,儲存方式是用兩個陣列來表示圖: 一個一維陣列儲存圖中頂點本身資訊
Caffe原始碼理解1:Blob儲存結構與設計
Blob作用 A Blob is a wrapper over the actual data being processed and passed along by Caffe, and also under the hood provides synchronization capability b
Oracle邏輯儲存結構與物理儲存結構
Oracle邏輯儲存結構包括表空間,各種段,區間,資料塊等幾種基本結構。 1)表空間是資料庫的邏輯劃分,每個資料庫至少有一個表空間,USER表空間供一般使用者使用,RBS表空間供回滾使用,一個表空間只能屬於一個數據庫。每一個表空間由同一磁碟上的一個或多個數據檔案組成。表空
圖的結構與操作
圖的結構 1、鄰接矩陣結構 #define MAXSIZE 100 #define INFINITY 65535 //無窮大,表示兩點直接沒有路徑連線 typedef struct Mgraph{ char vex[MAXSIZE]; //定義頂點陣列 int a
InnoDB引擎--儲存結構與檔案
資料庫是資料的集合,資料庫管理系統(DBMS)是操作和管理資料庫的應用程式。資料庫應用主要有兩類:OLAP(聯機分析處理)和OLTP(聯機事務處理)。 OLAP的主要特點是: 實時性要求不高 資料量大 併發量小 OLTP的主要特點是: 實時性要求高
資料的儲存結構與邏輯結構
資料儲存結構比較 順序結構:一段連續的記憶體空間。 優點:隨機訪問 缺點:插入刪除效率低,大小固定 鏈式結構:不連續的記憶體空間 優點:大小動態擴充套件,插入刪除效率高 缺點:不能隨機訪問。 索引結構:為了方便查詢,整體無序,但索引塊之間有序
資料結構知識點--儲存結構與邏輯結構
1. 資料的邏輯結構 邏輯結構是指資料元素之間的邏輯關係,即從邏輯關係上描述資料。它與資料的儲存無關,是獨立於計算機的。資料的邏輯結構分為線性結構和非線性結構,線性表是典型的線性結構;集合、樹和圖是典型的非線性結構。資料的邏輯結構分類見圖1-1。 集合結構中的資料元素之間除了 “同屬於一個集合”的關係外,別
17-看圖理解資料結構與算法系列(NoSQL儲存-LSM樹)
關於LSM樹 LSM樹,即日誌結構合併樹(Log-Structured Merge-Tree)。其實它並不屬於一個具體的資料結構,它更多是一種資料結構的設計思想。大多NoSQL資料庫核心思想都是基於LSM來做的,只是具體的實現不同。所以本來不打算列入該系列,但是有朋友留言了好幾次讓我講LS
圖的儲存結構(鄰接矩陣與鄰接表)及其C++實現
一、圖的定義 圖是由頂點的有窮非空集合和頂點之間邊的集合組成,通常表示為: G=(V,E) 其中:G表示一個圖,V是圖G中頂點的集合,E是圖G中頂點之間邊的集合。 注: 線上性表中,元素個數可以為零,稱為空表; 在樹中,結
圖的儲存結構:鄰接矩陣與鄰接表(稠密圖與稀疏圖)
稠密圖用 鄰接矩陣儲存 稀疏圖用 鄰接表儲存 原因: 鄰接表只儲存非零節點,而鄰接矩陣則要把所有的節點資訊(非零節點與零節點)都儲存下來。 稀疏圖的非零節點不多,所以選用鄰接表效率高,如果選用鄰接矩陣則效率很低,矩陣中大多數都會是零節點! 稠密圖的非零界點多,零節點少,選
資料結構與演算法16-圖的儲存結構
圖的儲存結構 圖的儲存結構相較線性表與樹來說就更加複雜了。首先,我們口頭上說的“頂點的位置”或“鄰接點的位置”只是一個相對的概念。其實從圖的邏輯結構定義來看,圖上任何一個頂點都可被看成是第一個頂點,任一頂點的鄰接點之間也不存在次序關係。如下圖 用之前學過的資料結構來表
