開門見山，本篇部落格就介紹圖相關的東西。圖其實就是樹結構的升級版。上篇部落格我們聊了樹的一種，在後邊的部落格中我們還會介紹其他型別的樹，比如紅黑樹，B樹等等，以及這些樹結構的應用。本篇部落格我們就講圖的儲存結構以及圖的搜尋，這兩者算是圖結構的基礎。下篇部落格會在此基礎上聊一下最小生成樹的Prim演算法以及克魯斯卡爾演算法，然後在聊聊圖的最短路徑、拓撲排序、關鍵路徑等等。廢話少說開始今天的內容。

一、概述

在部落格開頭，我們先聊一下什麼是圖。在此我不想在這兒論述圖的定義，當然那些是枯燥無味的。圖在我們生活中無處不在呢，各種地圖，比如鐵路網，公路網等等這都是典型的圖形結構。來點直觀的，我們就以北京的地鐵為例。如果你在北京坐過地鐵，那麼對下方的這張圖並不陌生。下方就是一個典型的圖形結構，而且還是連通圖呢。也就是說，你從任意一個地鐵站進去，就可以在其他相連的地鐵站出來。

下方每個地鐵站就是圖的結點，地鐵站與地鐵站之間的連線就是圖的弧，如果我們給弧新增上距離，那麼這個距離就是這個弧所對應的權值。比如我們舉個例子，假如大望路站到國貿站的距離是1.5公里。那麼我們翻譯成我們圖中的術語就是大望路結點到國貿結點有一條弧，這條弧的權值是1.5公里。當然，從大望路到國貿有多條路徑，那麼那條路徑最近呢，這就是我們後面要說的最優路徑了。我們如果想連通每個站點，並且想連線每個站點的權值的和最小，那麼就是我們以後要聊的最小生成樹了。

今天我們部落格的主題就是如果去儲存下方這種型別的圖，然後對圖中的節點進行遍歷。當然儲存的時候我們要儲存弧度所對應的權值。

當然，上面這個地鐵站的地鐵是比較複雜的，我們就簡單畫一個圖，來模擬一下上述圖的結構即可。然後將該結構進行儲存。然後再基於該儲存結構對圖進行遍歷。圖的物理儲存結構可以分為鄰接矩陣和鄰接連結串列的形式。則圖的搜尋分為廣度優先搜尋（BSF -- Breadth First Search）

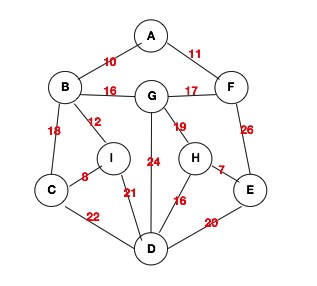
二、鄰接矩陣

接下來我們就將上面這個圖儲存下來，當然是使用我們上面提到過的鄰接矩陣或者鄰接連結串列來儲存。在構建圖之前呢，我們依然要先定義圖的協議，因為圖的物理儲存結構分為鄰接矩陣和鄰接連結串列。不同的儲存方式也就對應著構建圖的方式不同，那麼圖的BFS與DFS的具體實現也是不同的，但是對外的介面是一致的。還是那句話，面向介面程式設計。所以我們要先定義完圖的相關介面，然後在給出具體實現。

1.圖的介面的定義

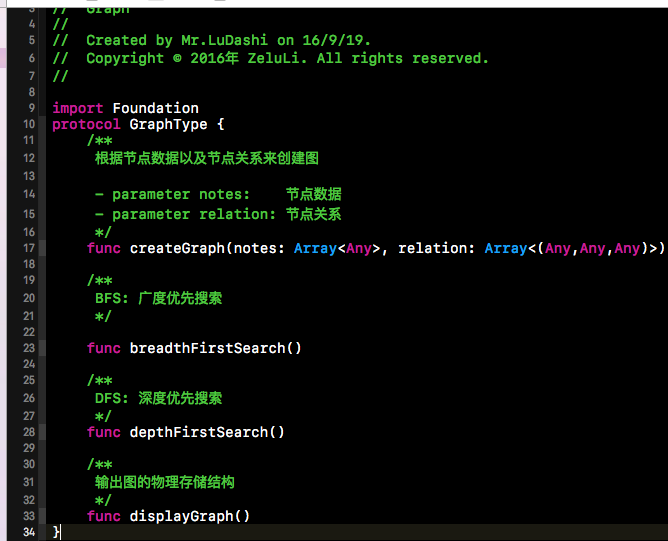
下方程式碼片段就是我們圖結構的協議，所有定義的圖結構都要遵循下方的協議。createGraph()

還是那句話，因為圖對外的呼叫介面是一致的，所以我們對於不同的物理儲存結構的圖，我們可以使用同一個測試用例。定義好了下方的協議後，我們就可以根據圖的物理儲存結構，給出具體實現了。

2、圖中關係的輸入

要想構建上面的圖的結構，我們得根據圖所提供的資訊來構建相應物理結構的圖。下方就是我們在構建圖結構時，所輸入的資訊。allGraphNote陣列中儲存的是圖中的所有結點，就類似於某個地鐵站的名字。而relation陣列中儲存的就是結點之間的資訊。其中一個元組就是一個結點間的關係。(A, B, 10)就說明A到B有條弧，該弧的權值是10，類似於大望路到國貿有條地鐵，距離是1.5一樣。我們就可以根據下方的這個資訊來構建我們想構建的圖了。

當然下方資訊在鄰接矩陣和鄰接連結串列中的儲存方式是不同的，下方會詳細介紹。 而上面我們提到的createGraph()方法中的兩個引數，就是下方這兩個陣列。

3.鄰接矩陣的構建

鄰接矩陣是儲存圖結構的一種物理儲存方式，其實說白了鄰接矩陣就是一個二維陣列，這個二維陣列中儲存的是圖中節點的關係。下方這個截圖就是上述圖結構的鄰接矩陣的儲存方式。節點與節點中間如果沒有弧的話，那麼權值就是0。如果兩個節點間有關係的話，那麼其中儲存的就是該弧上的權值，具體如下所示。

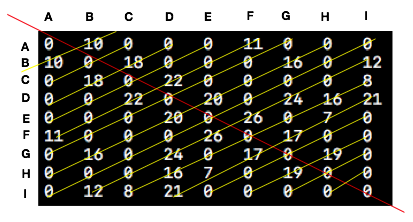
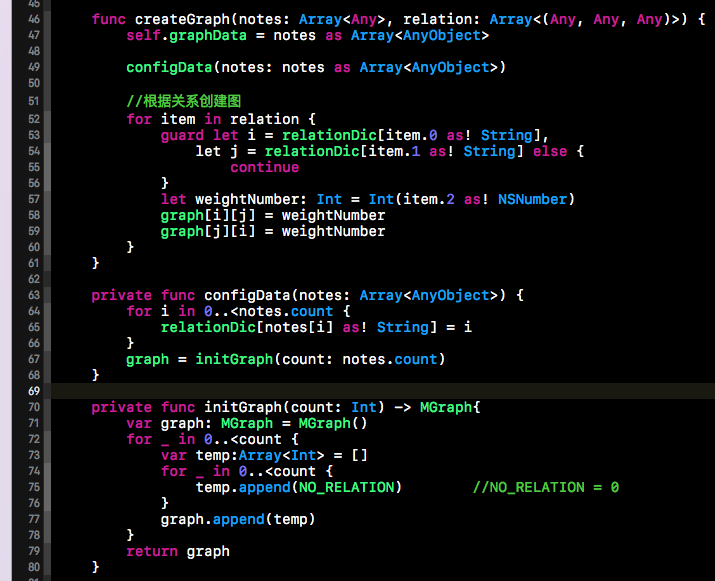
根據上面這個結構，我們就開始我們的程式碼實現了，下方就是我們建立鄰接矩陣相應的程式碼。createGraph()方法的第一個引數是我們上面提到過的allGraphNote，也就是圖中所有的結點集合。第二個引數則是上面我們提到過的relation，其中儲存的就是圖中結點間的關係。下方的initGraph()方法負責儲存圖的鄰接矩陣的初始化，而relationDic中儲存的就是圖的結點與鄰接矩陣下標的對應關係。通過下方這三個函式，我們就可以構建出上面圖結構所對應的鄰接矩陣了。

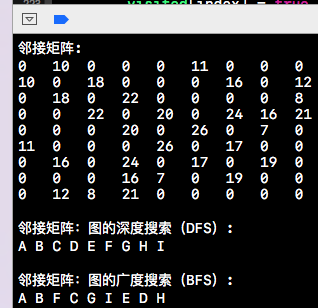
上面這個矩陣其實就是下方這段程式碼構建的圖結構的輸出結果。通過輸出結果可以看出，上面的鄰接矩陣以紅線為中心軸對稱。因為A到B的的權值為10，那麼B到A的權值也是10，所以會形成上述對稱結構。這個在我們對圖的遍歷時需要注意一下該對稱結構。

4.鄰接矩陣的廣度優先搜尋（BFS）

上面建立完鄰接矩陣後，我們就開始對此鄰接矩陣進行操作了。接下來要乾的事情就是對上面的鄰接矩陣進行廣度優先搜尋（Breadth Frist Search）。在之前二叉樹的層次遍歷中我們提到過，二叉樹的層次遍歷與圖的廣度優先搜尋就是一個東西。接下來我們仔細的聊聊。圖的廣度優先搜尋要藉助我們之前聊的佇列。該佇列中記錄的就是上次遍歷那一層節點，下次遍歷結點的順序就按照佇列中記錄的節點的順序來。下方就是廣度搜索的示意圖。

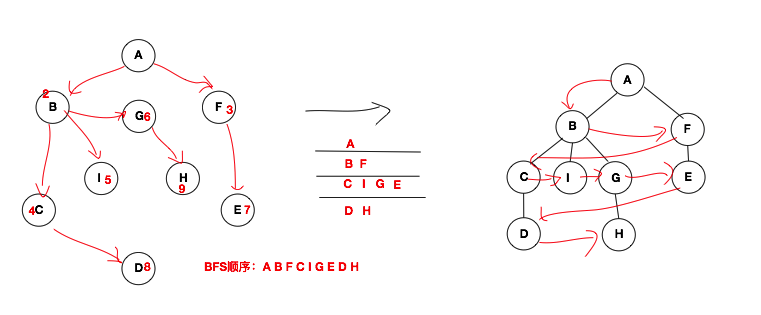
上面BFS示意圖中，是以A為首結點來進行的廣度優先搜尋。廣度優先搜尋的思想是藉助佇列“一層一層的輸出”。在遍歷一個點後，那麼就將與該結點相連並未遍歷的點加入佇列，下次輸出的點從佇列中獲取，然後再輸出，不斷的重複這個過程。從描述中我們可以看出，此過程可以使用遞迴來解決。下方程式碼段就是鄰接矩陣的廣度優先搜尋的程式碼，如下所示：

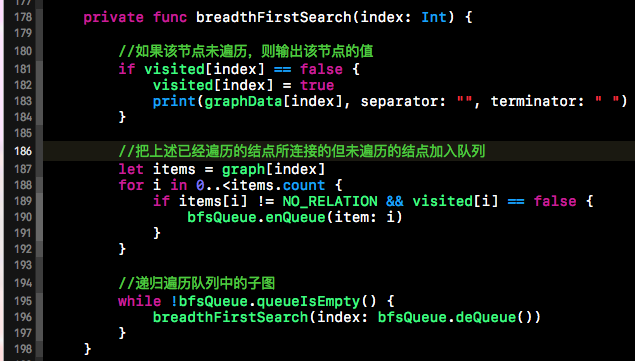
上面的程式碼並不複雜，上面用到的visited陣列用來標記當前遍歷的結點是否已經被遍歷過，因為上述的矩陣是對稱的。程式碼比較簡單，在此就不做過多贅述了。主要還是藉助佇列來保證層級關係。

5.鄰接矩陣的深度優先搜尋（Depth First Search）

接下來我們來聊深度優先搜尋--DFS。一句話總結DFS，其實就是“一條道走到黑，走不通，退一步再找道”。其實深度優先搜尋與之前我們聊的二叉樹的先序遍歷非常類似。在實現DFS時，如果不使用遞迴來實現的話，我們可以藉助棧的操作來實現。因為遞迴本來就是一個棧結構，所以直接可以使用遞迴來完成DFS。下方就是DFS的示意圖，下方的示意圖看明白了，用程式碼去實現也就不是什麼難事了。

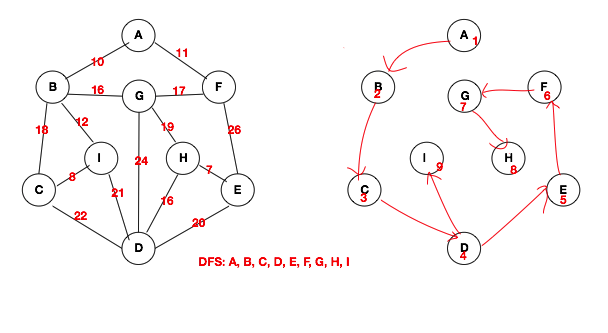
下方這個遞迴函式就是鄰接矩陣的DFS的實現，同樣會用到visited來標記結點是否被遍歷過。

6.測試用例

下方這段程式碼就是我們的測試用例，該測試用例函式的引數的型別是GraphType, 也就是我們之前定義的協議。只要是遵循該協議的類的物件都可以作為該函式的引數，所以我們下方這個測試用例是通用的。這也是面向介面程式設計的好處之一。

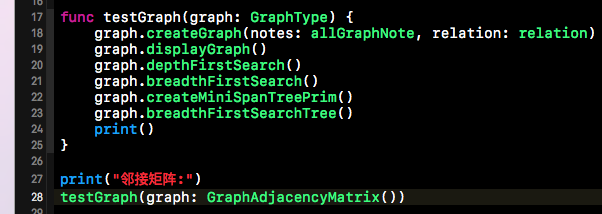
下方是上述程式碼的測試用例所輸出的結果，如下所示。當然該測試用例也同樣適用於鄰接連結串列實現的圖，前提是要遵循我們之前定義的協議。

三、鄰接連結串列

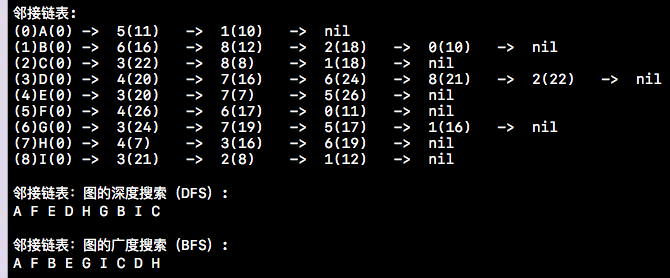
上面介紹完鄰接矩陣及其相關內容後，我們還要聊一下另一種圖的儲存結構----鄰接連結串列。鄰接連結串列就是陣列與連結串列的結合體，也就是將連結串列掛在一維陣列中。開門見山，下方就是鄰接連結串列測試用例所輸出的結果。前面的下標其實就是一個一維陣列，每個下標後方所跟的鏈就是掛在該下標後方的鏈。鏈中每個節點所儲存的內容是與該陣列下標所連線的結點的下標以及權值。下方這個鄰接連結串列儲存的就是上面我們那個圖。

雖然下方的DFS和BFS與上述鄰接矩陣中的DFS和BFS不同，但是規則是按照我們之前聊的規則來的。

1.鄰接連結串列的建立

上面也說了，鄰接連結串列就是將一個個的連結串列掛在一維陣列中。在建立鄰接連結串列之前，我們得先建立鄰接連結串列中連結串列所需的結點。下方這個就是我們鄰接連結串列中所需要的結點。data儲存的是所連結點在一維陣列中的index，weightNumber儲存的就是權值，preNoteIndex儲存的就是當前結點所在連結串列連線的一維陣列的index。next則指向連結串列中的下一個結點。

建立好我們需要的頭結點後，我們就該建立我們的鄰接連結串列了。下方程式碼段的createGraph()方法所需的引數與鄰接矩陣對應的方法所需的引數一致。下方函式中第一個迴圈是初始化一維陣列，將每個結點的資訊新增到一維陣列中，等待著與這些結點相連的結點掛在相應的鏈上。relationDic中記錄著結點與一維陣列索引的對應資訊。第二個迴圈是遍歷relation陣列，取出每個結點間的關係資訊，根據這些資訊將相應的結點掛在相應的一維陣列每個元素對應的鏈上。

2、鄰接連結串列的廣度優先搜尋（BFS）

鄰接連結串列的廣度優先搜尋與鄰接矩陣的廣度優先搜尋雖然演算法一致，但是由於其儲存資料的方式不同，具體實現起來還是有所不同的。因為是BFS, 所以，鄰接連結串列的BFS依然會藉助佇列來實現。下方我們採用了佇列加遞迴的方式來實現的BFS。

方法中最外層的if語句塊用來判斷當前方法傳入的索引所對應的結點是否已經被遍歷了，如果未被遍歷則輸出，輸出後將標誌位置為true。遍歷完當前結點後，將與該結點相連線的並且未被遍歷的結點進入佇列。然後再遞迴遍歷佇列中未被遍歷的結點。具體程式碼如下所示：

3、鄰接連結串列的深度優先搜尋（DFS）

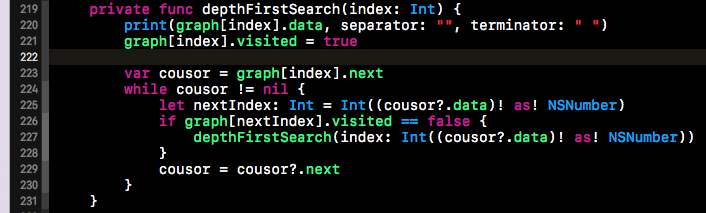
下方這段程式碼就是鄰接連結串列的深度優先搜尋，下方程式碼段沒有借用佇列，但是使用了遞迴。因為在遞迴呼叫函式的過程中，存在遞迴呼叫棧。棧有著先入後出的特點，上面我們在聊DFS時聊到，深度優先搜尋就是一直往下走，走不動了就回退一步繼續尋找可以往下走的路。這個一直往下走其實就是不斷push入棧的過程，而回退一步其實就是pop出棧的步驟。鑑於遞迴過程本身就是一個棧的結構，所以就不需要我們再建立一個棧來實現這個push和pop操作了。下方就是鄰接連結串列的DFS的相關程式碼。程式碼並不複雜，在此不做過多贅述了。

至此，圖的鄰接矩陣和鄰接連結串列的DFS、BFS就聊完了。當然本篇部落格往上貼的程式碼只是部分核心程式碼，完整的Demo已在github上進行分享。下方就是分享連結，下篇部落格會聊一下圖的最小生成樹的兩個演算法。今天部落格就先到這兒。