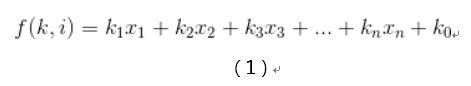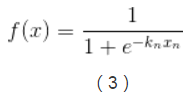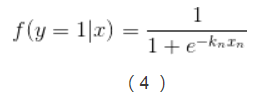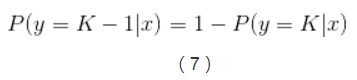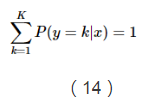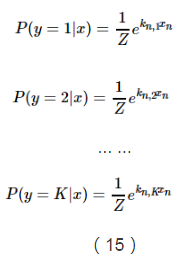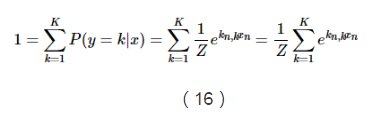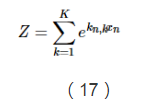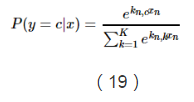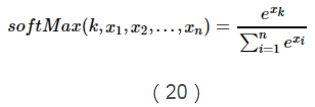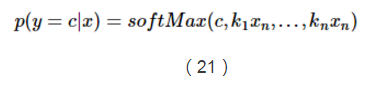多分類邏輯迴歸(Multinomial Logistic Regression)
前言
其中二分類是最常見且使用最多的分類場景,解決二分類的演算法有很多,比如:
簡介
在統計學裡,多類別邏輯迴歸是一個將邏輯迴歸一般化成多類別問題得到的分類方法。用更加專業的話來說,它就是一個用來預測一個具有類別分佈的因變數不同可能結果的概率的模型。
另外,多類別邏輯迴歸也有很多其它的名字,包括polytomous LR,multiclass LR,softmax regression,multinomial logit,maximum entropy classifier,conditional maximum entropy model。
在多類別邏輯迴歸中,因變數是根據一系列自變數(就是我們所說的特徵、觀測變數)來預測得到的。具體來說,就是通過將自變數和相應引數進行線性組合之後,使用某種概率模型來計算預測因變數中得到某個結果的概率,而自變數對應的引數是通過訓練資料計算得到的,有時我們將這些引數成為迴歸係數。
模型分析
1、線性分類器
多分類邏輯迴歸使用的是跟線性迴歸一致的線性預測函式,其基本表示式如下:
其中i=[1,n]這裡的k是一個迴歸係數,它表示的是第n個觀測變數/特徵對地n個結果的影響有多大。這裡將1看做x0,我們可以得到上述公式的向量化形式:

這裡kn是一個迴歸係數向量,表示的是觀測向量xi表示的觀測資料對結果k的影響度,或者叫重要性。
2、邏輯迴歸
多分類邏輯迴歸是基於邏輯迴歸(Logistic Regression)來做的,邏輯迴歸的基本表示如下:
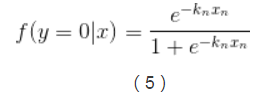
3、k-1個獨立二元邏輯迴歸到多分類邏輯迴歸的擴充套件
實現多類別邏輯迴歸模型最簡單的方法是,對於所有K個可能的分類結果,我們執行K−1個獨立二元邏輯迴歸模型,在執行過程中把其中一個類別看成是主類別,然後將其它K−1個類別和我們所選擇的主類別分別進行迴歸。通過這樣的方式,如果選擇結果K作為主類別的話,我們可以得到以下公式。

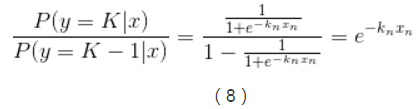

在公式(6)中已經引入了所有可能的迴歸係數集合,對公式(6)兩邊進行指數化處理,能夠得到以下公式:


這樣我們就能計算出所有給定未預測樣本情況下某個結果的概率,如下:

迴歸引數的估計
上面篇幅所涉及到的每一個權重向量kn中的未知係數我們可以通過最大後驗估計(MAP)來計算,同時也可以使用其它方法來計算,例如一些基於梯度的演算法。
二元邏輯迴歸對數模型到多分類邏輯迴歸的擴充套件
在上文中提到了由K-1個獨立二元迴歸到多分類邏輯迴歸的擴充套件,這裡介紹另外一種多分類邏輯迴歸的擴充套件——使用線性預測器和額外的歸一化因子(一個配分函式的對數形式)來對某個結果的概率的對數進行建模。

這裡用一個額外項-ln(Z)來確保所有概率能夠形成一個概率分佈,從而使得這些概率的和等於1。
由於上面說到,所有概率之和等於1,因此我們可以得到Z的推導公式:

這個函式能夠將x1,...,xn之間的差別放大,當存在一個xk比所有值中的最大值要小很多的話,那麼它對應的softMax函式值就會區域0。相反,當xk是最大值的時候,除非第二大的值跟它很接近,否則的話softMax會趨於1。所以softmax函式可以構造出一個像是平滑函式一樣的加權平均函式。
所以,我們可以把上面的概率公式寫成如下softMax函式的形式:
至此,多分類的邏輯迴歸形式以及介紹完了,後續會進行最大似然函式的學習,敬請期待!