今天，恰好遇到使用matlab進行了非線性方程組的求解。

情況是，一些無法手動表示，推導的方程組，比如像超越方程這種，可以用matlab進行直接求值，這在一些需要模擬資料的場景比較有用。

環境：matlab2015a

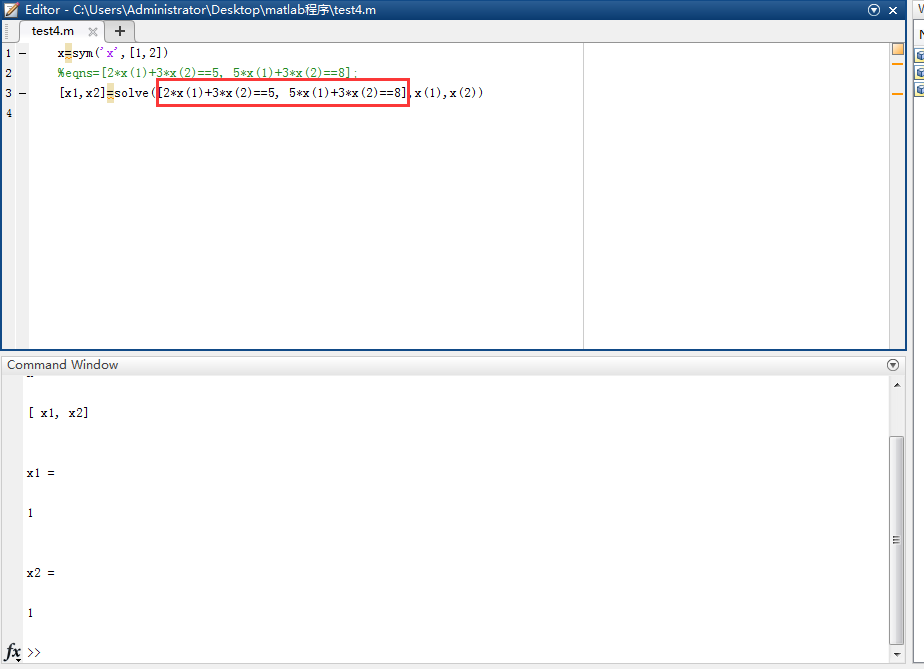
函式：Symbolic Math Toolbox裡面的sym和solve函式。其中sym在第一個紅框中，solve在第二個紅框中。

1.solve

格式：（1）Y = solve(eqns,vars)

（2）[y1,...,yN] = solve(eqns,vars)

先解釋兩個引數吧，

①eqns就是你的方程組，方程組裡面的各個方程是組織為一個數組的。

所以你可以直接使用 [方程1，方程2，。。。。，方程n] 對應於eqns輸入引數。

也可以後面會將到，將eqns宣告為一個數組，然後帶入eqns輸入即可，這樣方便編輯。

②vars就是你想要返回的求得的未知變數，如果你不明確指定，那他就會按照sym的對應。

③返回值，有兩種。Y代表一個結構體，將返回的變數通通放入結構體Y裡面，然後訪問和C語言的結構體一樣，假設Y下面有兩個成員，y1，y2，

你直接Y不會顯示裡面的值，要Y.y1 Y.y2才能顯示。

[y1,y2,...,yN]就是直接對應於vars裡面你直接想要求得的值，如果沒有明確指定vars就按預設對應。

注：（1）vars如果你不明確指定的話，在引數少的時候也容易分清返回自己想要的，但是如果引數過多還是最好明確指定自己想要的引數。

（2）Y和[y1,y2,...,yN]兩種返回賦值方式各有優缺點，Y你訪問裡面的元素的話比較麻煩，

[y1,y2,...,yN]這種情況如果N有幾十個，你這樣輸入很煩，而這個時候全部存入Y中，再用一個for迴圈遍歷就能存入一個向量中了。

（3）然而突然發現，在結構體中的元素並不能使用下標來遍歷，目前還在糾結中。。。

2.sym

先講下這個函式用來幹什麼的，在matlab中，你可以直接用變數，但是你必須要賦值。

比如你想要輸入a=b+c;

你的a和b首先要初始化，即b和c是要有值的。

那麼問題就來了，我求解方程的時候就是不知道未知數才求解，如何賦值呢？

這個時候就需要使用sym宣告符號變量了。它宣告的未知量不用賦值。

格式：A = sym('a',[m,n])

這個的意思就是說，生成一個m，n維的矩陣A，然後它的每一個元素用a來標識。

注意：用a的標識是它標識矩陣內部的元素，你要使用該未知量還是需要按照正常的矩陣元素訪問方法，比如A（1,2）這樣。

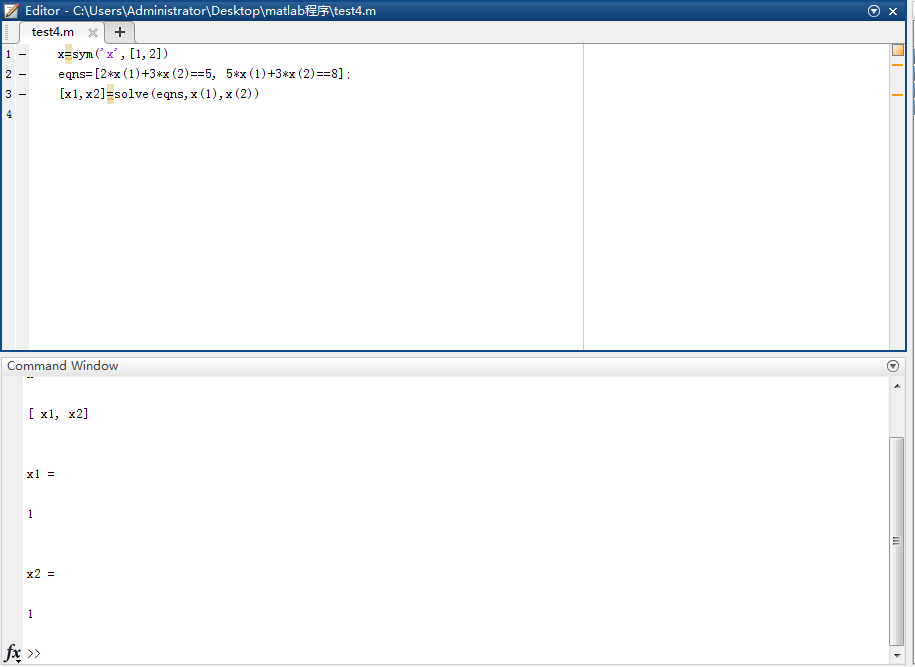
3.舉個栗子

求解方程組：3x1+2x2=5

                      5x1+3x2=8

（1）求解

（2）直接使用 [方程1，方程2] 作為solve的引數

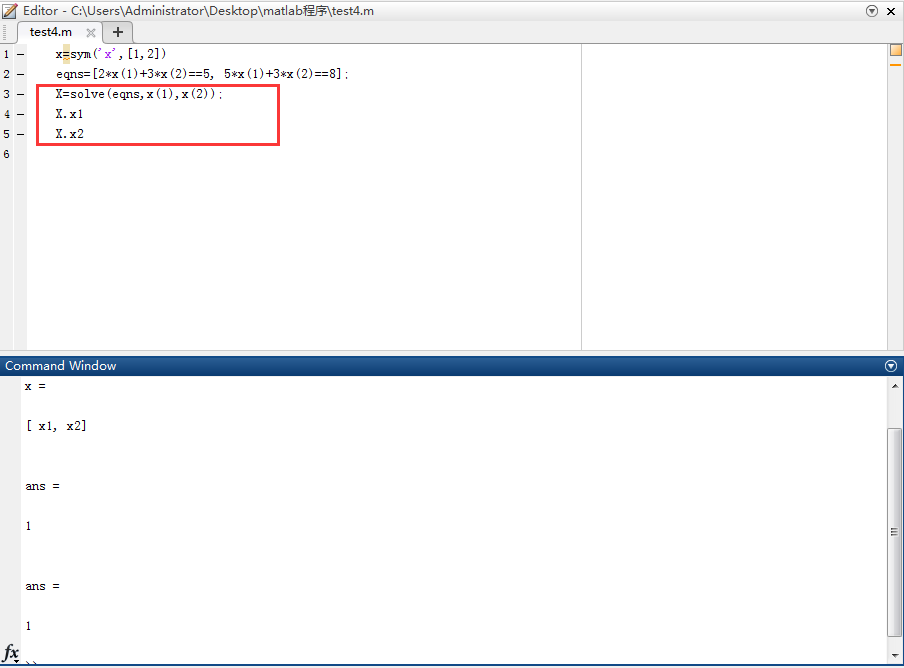
（3）用結構體返回值的形式