1. 基本概念

路徑長度：樹中一個結點到另一個結點路徑上的分支數目。
樹的路徑長度：從樹根到每一結點的路徑長度之和。
帶權路徑長度：結點到樹根之間的路徑長度與結點上權的乘積。
樹的帶權路徑長度（WPL）：樹中所有葉子結點的帶權路徑長度之和。
郝夫曼樹（最優二叉樹）：對於一棵有n個葉子結點的二叉樹，帶權路徑長度最小的二叉樹。

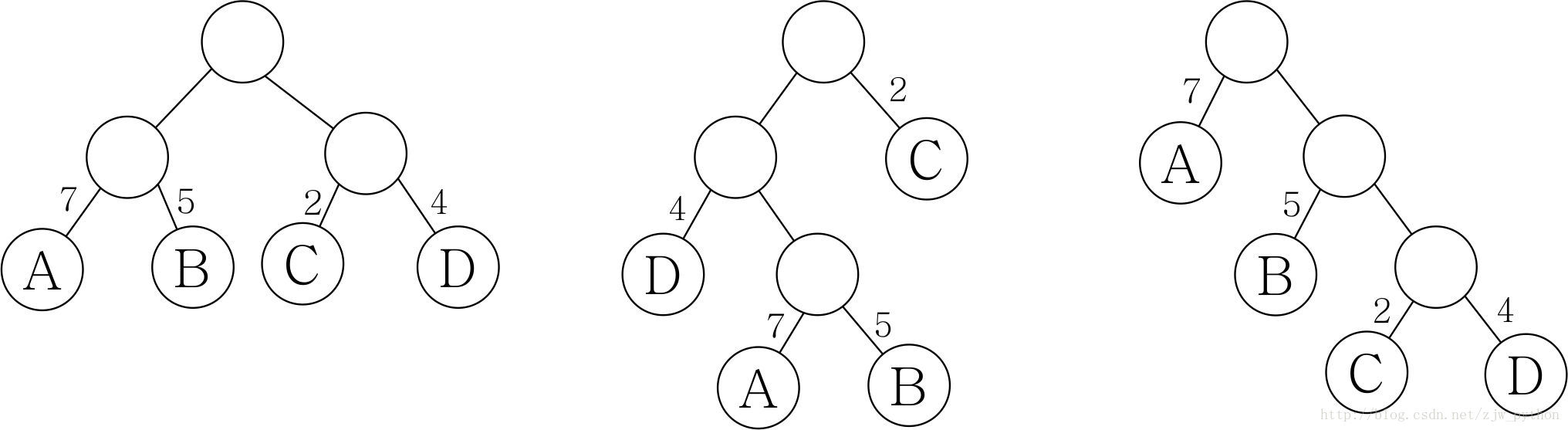
第一棵樹 WPL=7*2+5*2+2*2+4*2=36
第二棵樹 WPL=7*3+5*3+2*1+4*2=46
第三棵樹 WPL=7*1+5*2+2*3+4*3=35
上述二叉樹中，第三棵樹帶權路徑長度最小，可以驗證，第三棵樹恰為郝夫曼樹。

2.郝夫曼樹的構造方法

假如現有4個權值，分別為a=7, b=5, c=2, d=4
1. 先把有權值的葉子結點按照權值從小到大排列成一個有序序列。即c, d, b, a。
2. 取頭兩個最小的權值的結點作為一個新節點N1的兩個子節點，其中權值較小的為左孩子，權值較大的為右孩子，新節點的權值為兩孩子結點的權值之和，即N1=c+d=2+4=6。
3. 用N1替換c和d，插入有序序列中，保持從小到大排列。
4. 重複步驟2，直到序列中只存在一個結點，該結點即為根結點。

3.郝夫曼編碼

例如有一段文字內容“BADCADFEED”，用相應的二進位制資料表示：
A：000， B：001，C：010，D：001，E：100，F：101

編碼後的資料為“001000011010000011101100100011”，很長的一段碼

但是在實際中，有的字母用的頻率很高，例如“a”，而有些字母則不常用，例如“x”
假設六個字母的平均使用頻率為 A 27%，B 8%，C 15%，D 15%，E 30%，F 5%，可以將其作為權值，構造一顆郝夫曼樹，並將左分支改為0，右分支改為1

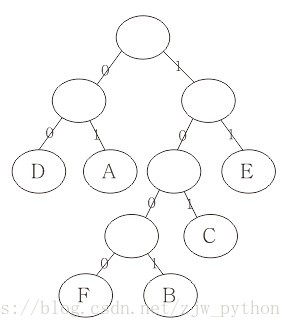
根據每個字母所經過的路徑重新編碼後，六個字母為 A：01，B：1001，C：101，D：00，E：11，F：1000。我們可以看到，重新編碼後，使用頻率較高的字母編碼長度變小了，而使用頻率較低的字母，編碼則加長了

原來的文字內容 “BADCADFEED”重新編碼為“1001010010101001000111100”，比原來少了5個字元，節約了約17%的傳輸成本。