CART演算法的原理以及實現

CART

分類迴歸樹(classification and regression tree，CART)模型由Breiman等人在1984年提出，是應用廣泛的決策樹學習方法。CART同樣由特徵選擇、樹的生成以及剪枝組成，既可以用於分類也可以用於迴歸。同樣屬於決策樹的一種。

CART演算法採用的是一種二分遞迴分割的技術，將當前樣本分成兩個子樣本集，使得生成的非葉子節點都有兩個分支。因此CART實際上是一顆二叉樹。

輸入：訓練資料集D
輸出：迴歸樹 $f (x)$
在訓練資料集所在的輸入空間中，遞迴得將每一個區域劃分為兩個子區域並決定每個子區域上的輸出值，構建二叉決策樹：
(1)選擇最優切分變數j和切分點s，求解

m i n_{j, s} [m i n_{c_{1}} \sum_{x_{i} \in R_{1} (j, s)} (y_{i} - c_{1})^{2} + m i n_{c_{2}} \sum_{x_{i} \in R_{2} (j, s)} (y_{i} - c_{2})^{2}]

遍歷變數j，對固定的切分變數j掃描切分點s，選擇使上式達到誤差最小的變數(j,s)，其中

R_{1}

和

R_{2}

表示的是劃分之後的空間。

(2)用選定的(j,s)劃分區域並決定響應的輸出值。

R_{1} (j, s) = {x^{(j)}} \leq s, R_{2} (j, s) = {x | x^{(j)} > s}

c_{m} = \frac{1}{N_{m}} \sum_{x_{i} \in R_{m} (j, s)} y_{i}, x \in R_{m}, m = 1, 2

(3)繼續對兩個子區域呼叫步驟(1),(2),直到滿足停止條件。

(4)將輸入空間劃分為M個區域 $R_{1}, R_{2}, R_{3} . . . . R_{M}$ ，生成決策樹：

f (x) = \sum_{m = 1}^{M} c_{m} I (x \in R_{m})

上面的演算法過程有點難以理解。下面我們舉出一個例子方便理解。

看電視時長	婚姻狀況	職業	年齡
3	未婚	學生	12
4	未婚	學生	18
2	已婚	老師	26
5	已婚	上班族	47
2.5	已婚	上班族	36
3.5	未婚	老師	29
4	已婚	學生	21

下面我們將利用上面的資料對年齡進行預測。

首先將j的屬性選為職業，則有三種劃分情況{“老師”，“學生”}、{“上班族”}以及{“老師”，“上班族”}、{“學生”}，最後一種為{“學生”，“上班族”}、{“老師”}

(1)第一種情況 $R_{1}$ ={“學生”}， $R_{2} =$ {“老師”，”上班族”}

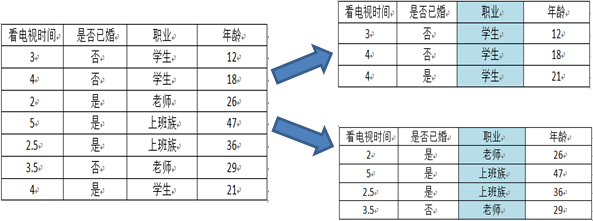
這裡寫圖片描述
此時有

c_{1} = (12 + 18 + 21) / 3 = 17

c_{2} = (26 + 47 + 36 + 29) / 4 = 34.5

m = m i n [\sum_{y_{i} \in R_{1}} (y_{i} - c_{1})^{2} + m i n \sum_{y_{i} \in R_{2}} (y_{i} - c_{2})^{2}]