DeepLabv1補充:對全連線條件隨機場(Fully Connected / Dense CRF)的理解
阿新 • • 發佈:2019-01-14
1. 隨機場 (random field)
由若干位置組成的整體,每一個位置按某種分佈隨機地賦一個值,全體即組成一個隨機場。
2. 馬爾科夫隨機場(MRF)
馬爾科夫隨機場是隨機場的特例,假設某一個位置的賦值只與和它相鄰的位置相關。
3. 條件隨機場(CRF)
條件隨機場是馬爾科夫隨機場的特例,假設馬爾可夫隨機場只有X和Y兩個隨機變數,一般情況下,X是給定的,Y是輸出。
形式化定義:設X和Y是隨機變數,
是給定X時Y的條件概率分佈,若Y構成一個馬爾科夫隨機場,則
是條件隨機場。
4. 線性鏈條件隨機場(linear CRF)
若X和Y有相同的結構,即
,則構成線性鏈(linear chain)條件隨機場。
形式化定義:設
均為線性連結串列示的隨機變數序列,在給定隨機變數序列X的情況下,如果隨機變數Y的條件概率分佈
構成條件隨機場,即具有馬爾科夫性,即:
則$P(Y|X)是線性鏈條件隨機場
5. 全連線條件隨機場(Fully Connected / Dense CRF)
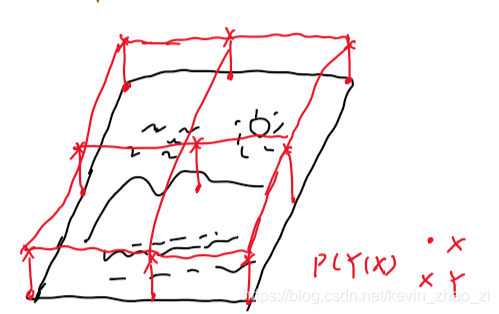
如下圖,有一幅影象:
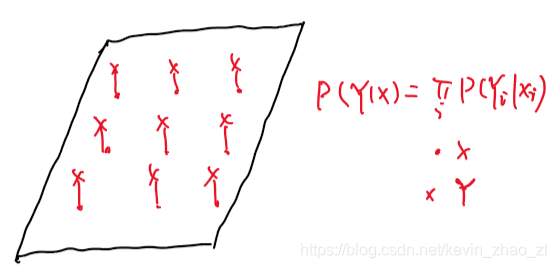
若畫素類別之和自己所在的畫素點有關,則建模如下圖:
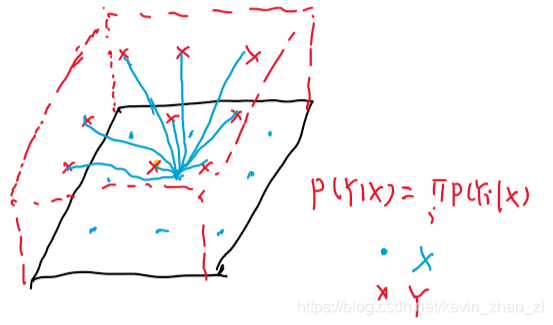
更加複雜地,每一個畫素類別和影象中所有畫素有關,則如下圖:
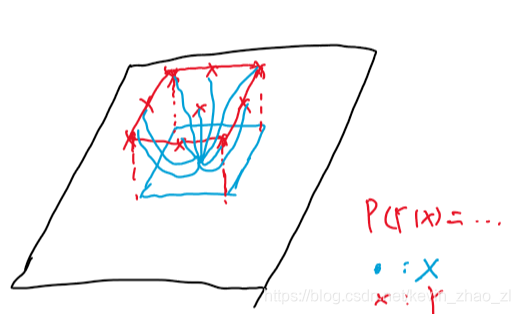
更加fancy的,每一個畫素類別和它的一個4鄰域相關,如下圖所示:
最複雜的,把能連的都連起來,構成全連線CRF,即Dense CRF。下圖並沒有畫全所有連線: