動態規劃 線性dp
動態規劃通常是用來解決最優化問題的。
一:斐波那契數列
對於斐波那契數列遞迴和非遞迴,可以參考這篇部落格:https://mp.csdn.net/postedit/79280467
如果用遞迴寫斐波那契數列,有很多重複計算值,導致時間複雜度大,可以用記憶搜尋。記憶搜尋是將已經計算過的值記錄下來,即用空間換時間。
//a[]來記錄每個斐波那契值
int fib(int n)
{
if (n == 1 || n == 2)
return a[n] = 1;
if (a[n] == 0)
return a[n] = fib(n - 2) + fib(n - 1 斐波那契的轉換
例1:有一人要爬n階的樓梯,他一次可以爬1階或2階,問要爬完這n階樓梯,共有多少種方法?
假設我們現在在第n階階梯上,顯然,我們上一步是在n-1階或者n-2階,我們可以知道,第n階的方法=n-1階的方法+n-2階的方法
同樣的,對於n-1階和n-2階我們也可以用類似的方法進行求解。
而當我們求到1階和2階的時候,顯然方法種數分別為1、2。
所以如果f[i]表示爬到第i階的方法數,那麼
f[1]=1 f[2] = 2
f[i] = f[i - 1]+ f[i - 2]
例2:在2×n的一個長方形方格中用一個1×2的積木鋪滿方格輸入n 輸出鋪放方案的總數.
例如n=3時為2×3方格,積木的鋪放方案有三種如下圖:
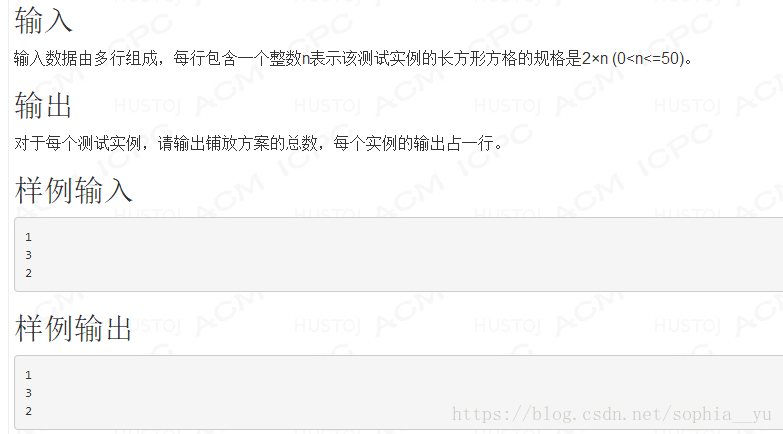
思路為:
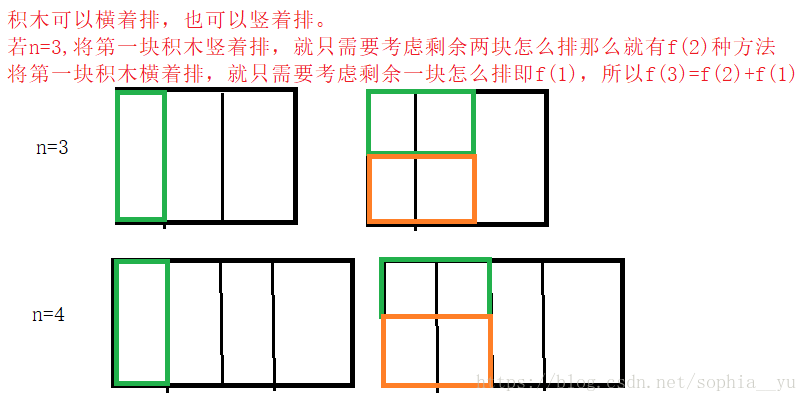
所以排積木是斐波那契的轉換。
程式碼如下:
//用long long是因為當n=50數值會超整型範圍
long long result[55] ;
long long jimu(int n)
{
if (n == 1 || n == 2)
return result[n] = n;
if (result[n] == 0)//該值沒有算過
return result[n] = jimu(n - 1) + jimu(n - 2);
else
return result[n];
}
int main()
{
int 例1:數字三角形
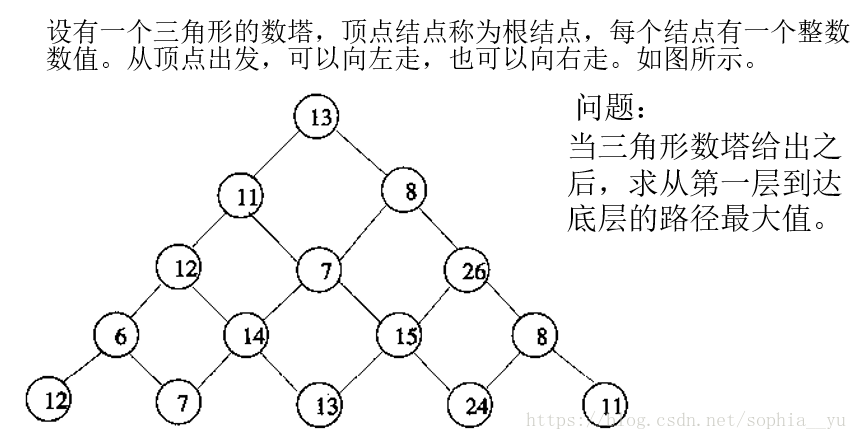
可以將三角形轉化為下三角形即
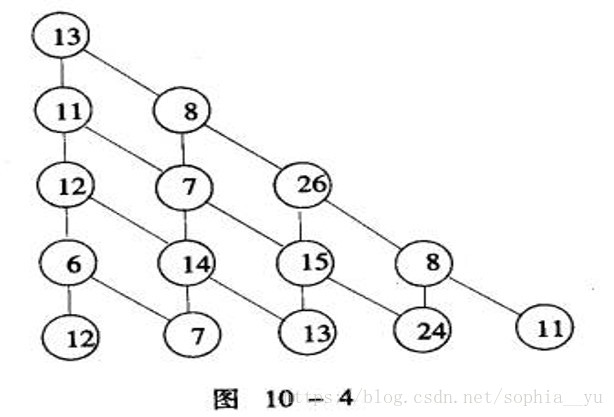
這樣就是向下走或者向右下走,求第一層到最低層路徑最大值,可以先求出頂元素向下走最大還是向右下走最大,即dp[1][1]=max(dp[2,1],dp[2,2])+arr[1][1],dp[i][j]表示該位置向底層走路徑的最大值,那麼dp[2,1]=max(dp[3,1],dp[3,2])+arr[2,1]….直至i=n到達最底層,用記憶化搜尋數字三角形程式碼如下:
#include<stdio.h>
#include<stdlib.h>
int n = 0;//n代表數字三角形行數
int arr[100][100] = { 0 };//arr[][]是數字三角形原始資料
int dp[100][100] = { 0 };//dp[][]是該位置到底層路徑最大值
//定義成全域性方便maxlen()函式操作
int maxlen(int x, int y)
{
if (x == n)
return arr[x][y];
if (dp[x][y] == -1)
return dp[x][y] = max(maxlen(x + 1, y), maxlen(x + 1, y + 1)) + arr[x][y];
else
return dp[x][y];
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)//二維陣列從1開始
{
for (int j = 1; j <= i; j++)
{
scanf("%d", &arr[i][j]);
dp[i][j] = -1;//架構每個位置路徑最大值初始化為-1.為記憶搜尋做準備
}
}
printf("%d\n", maxlen(1, 1));//指從arr[1][1]到底層路徑最大值
system("pause");
return 0;
}遞推數字三角形
#include<stdio.h>
#include<stdlib.h>
int main()
{
int n = 0;//n代表數字三角形行數
int arr[100][100] = { 0 };//arr[][]是數字三角形原始資料
int dp[100][100] = { 0 };//dp[][]是該位置到底層路徑最大值
scanf("%d", &n);
for (int i = 1; i <= n; i++)//二維陣列從1開始
{
for (int j = 1; j <= i; j++)
{
scanf("%d", &arr[i][j]);
dp[i][j] = arr[i][j];//架構每個位置路徑最大值初始化該位置原始值,為最底層最大值做準備
}
}
for (int i = n - 1; i >= 1; i--)
{ //底層元素認為是該位置路徑最大值
for (int j = 1; j <= i; j++)
{
dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + arr[i][j];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= i; j++)
printf("%d ", dp[i][j]);
printf("\n");
}
printf("%d\n", dp[1] [1]);//指從arr[1][1]到底層路徑最大值
system("pause");
return 0;
}
例2:滑雪
#include<stdio.h>
#include<stdlib.h>
int n = 0;
int arr[100][100];//每個點的高度
int maxlen(int x, int y)
{
//int Max = 1;
if (x > 0 && x <= n && y>0 && y <= n)
{
int Max = 1;
//假如該位置上邊點到坡底最長為m,該位置到坡底最長距離為m+1
if (arr[x - 1][y] < arr[x][y])//上
Max = max(maxlen(x - 1, y) + 1, Max);
if (arr[x + 1][y] < arr[x][y])
Max = max(maxlen(x + 1, y) + 1, Max);//下
if (arr[x][y + 1] < arr[x][y])//右
Max = max(maxlen(x, y + 1) + 1, Max);
if (arr[x][y - 1] < arr[x][y]) //左
Max = max(maxlen(x, y - 1) + 1, Max);
return Max;
}
return 0; //注意遞迴時,int型別返回時需要退出該函式需要有返回值,通常是0,對該題也是0
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
scanf("%d", &arr[i][j]);
}
}
int Maxlen = 0;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
Maxlen = max(Maxlen, maxlen(i, j));
}
}
printf("**************\n");
printf("%d\n", Maxlen);
system("pause");
return 0;
}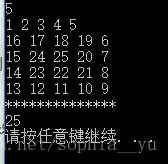
如果是用記憶化搜尋程式碼如下:
int n = 0;
int arr[100][100];//每個點的高度
int dp[100][100]; //每個點到坡底的最長距離
int maxlen(int x, int y)
{
if (x > 0 && x <= n && y > 0 && y <= n)
{
if (dp[x][y] != 0)
return dp[x][y];
dp[x][y] = 1;
if (arr[x - 1][y] < arr[x][y])//上
dp[x][y] = max(dp[x][y], maxlen(x - 1, y) + 1);
if (arr[x + 1][y] < arr[x][y])//下
dp[x][y] = max(dp[x][y], maxlen(x + 1, y) + 1);
if (arr[x][y + 1] < arr[x][y])//右
dp[x][y] = max(dp[x][y], maxlen(x, y + 1) + 1);
if (arr[x][y - 1] < arr[x][y]) //左
dp[x][y] = max(dp[x][y], maxlen(x, y - 1) + 1);
return dp[x][y];
}
return 0;
}
//但是首先得將dp[i][j]初始化為0,如下
for (int j = 1; j <= n; j++)
{
scanf("%d", &arr[i][j]);
dp[i][j] = 0;//為後面記憶化搜尋做準備
} 線性dp
一:最長不降序子序列的長度
#include<stdio.h>
#include<iostream>
using namespace std;
const int maxn = 1005;
int a[maxn];
int dp[maxn];
int main()
{
int n = 0;
while (scanf("%d", &n) != EOF)
{
//將資料輸入
for (int i = 0; i < n; i++)
{
scanf("%d", &a[i]);
}
//以i結尾的資料最大不降序子序列長度
for (int i = 0; i < n; i++)
{
dp[i] = 1;
for (int j = 0; j < i; j++)
{
if (a[j] <= a[i])
{
dp[i] = max(dp[j] + 1, dp[i]);
}
}
}
//輸出最大不降序子序列長度
int maxlen = 0;
for (int i = 0; i < n; i++)
{
maxlen = max(dp[i], maxlen);
}
printf("%d\n", maxlen);
}
system("pause");
return 0;
}例1:A國部署的反導系統遇到了一個致命BUG,那就是每一次發射的攔截導彈的飛行高度都將只能小於等於上一枚導彈的飛行高度,第一次發射的攔截導彈的飛行高度可以看作是足夠大。對於A國,這是一件很嚴重的問題,這意味著A國的防空系統面臨空前危機。通過對A國的軍事部門計算機的入侵,A國還不知道敵對國B國剛才已經發現了這項BUG。更不知道,在這項BUG的報告書上交到B國空軍司令部那一刻,三分鐘後B國的全體高階空軍軍官已經在作戰室討論作戰方案。如果戰爭真的開始,B國將依次派出n架戰鬥機A國將依次發射攔截導彈,這n架飛機的飛行高度分別是h1h2h3…..hn。B國將要充分利用這項漏洞,考慮到這麼一種情況,假設只要A國的導彈的飛行高度大於等於B國飛機就能百分之百地鎖定並擊落,那麼B國,最少將會有幾架不被擊落飛機?
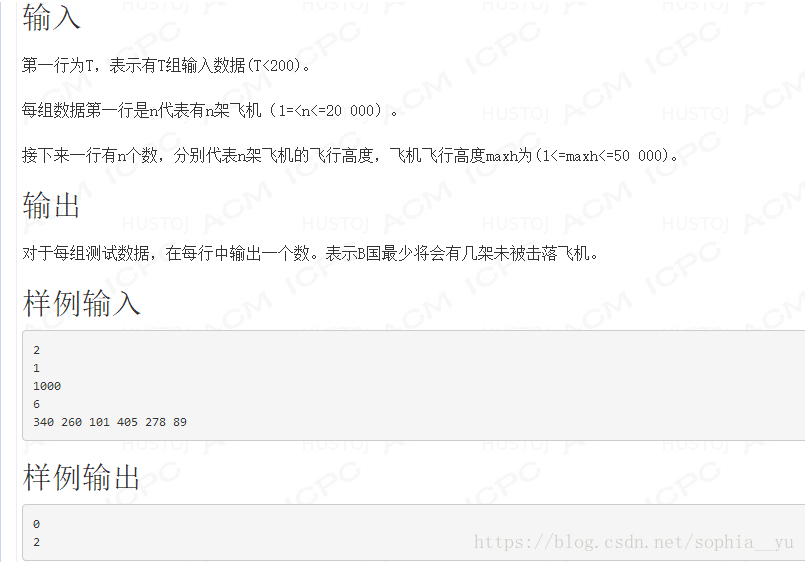
最少幾架不被擊落,即最多飛機被擊落,那麼該題可以轉化求最長不升序子序列長度。
程式碼如下:
#include<stdio.h>
#include<iostream>
using namespace std;
int main()
{
int T = 0;
scanf("%d", &T);
int a[20005] = { 0 };
int dp[2005] = { 0 };
while (T--)
{
int n = 0;
scanf("%d", &n);
for (int i = 0; i < n; i++)
{
scanf("%d", &a[i]);
}
for (int i = 0; i < n; i++)
{
dp[i] = 1;
for (int j = 0; j < i; j++)
{
if (a[j] >= a[i])
{
dp[i] = max(dp[j] + 1, dp[i]);
}
}
}
int maxlen = 0;
for (int i = 0; i < n; i++)
{
maxlen = max(dp[i], maxlen);
}
printf("%d\n", n - maxlen);
}
system("pause");
return 0;
}最長公共子序列


當j=0或i=0初始化為0:如果j=0,即X中沒有元素,如果i=0,即Y中沒有元素。
例1:渣渣輝從小的夢想就是當一名警察,做一名出色的反恐精英。
但是事與願違,他現在只能天天在家裡打 CF (codeforce) 了。
我們知道,CF上經常有比賽,渣渣輝這麼熱愛CF,當然一次也沒有落下。
比賽規則是這樣的:
1.有 N 種子彈型號,編號分別為 1,2 … N。
2.有 N 種恐怖分子型別,編號也分別為1,2 … N。
3.敵人有 M 個,子彈也會有 M 個。
4.只有一種子彈打中同種編號型別的敵人時,得分才會加 1 分。
5.子彈已經按照輸入順序裝填,恐怖分子也按照輸入順序出現。
你能幫助渣渣輝打到最高分嗎?
(渣渣輝射擊百發百中,他可以放空槍,也可以選擇不射擊某名恐怖分子)

遞推程式碼:
#include<include.h>
#include<stdlib.h>
const int Maxn = 100;
const int Maxm = 100;
int diren[Maxm];
int zidan[Maxm];
int dp[Maxm][Maxm];
int main()
{
int N = 0; //N 種類型的敵人和子彈
int M = 0; //M 個敵人和子彈
scanf("%d %d", &N, &M);
for (int i = 1; i <= M; i++)
{
scanf("%d", &diren[i]);
}
for (int i = 1; i <= M; i++)
{
scanf("%d", &zidan[i]);
}
for (int i = 0; i <= M; i++)
{
dp[0][i] = dp[i][0] = 0;//第i行和第j列初始化為0
}
for (int i = 1; i <= M; i++)
{
for (int j = 1; j <= M; j++)
{
if (diren[i] == zidan[j])
{
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
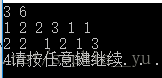
printf("%d\n",dp[M][M]);//最後一個肯定最大
system("pause");
return 0;
}遞迴程式碼:
#include<include.h>
#include<stdlib.h>
const int Maxn = 100;
const int Maxm = 100;
int diren[Maxm];
int zidan[Maxm];
int dp[Maxm][Maxm];
int maxlen(int x,int y)
{
if (x == 1)//遞迴出口
return 0;
if (dp[x][y] == 0)
{
if (diren[x] == zidan[y])
return dp[x][y] = maxlen(x - 1, y - 1) + 1;
else
return dp[x][y] = max(maxlen(x , y - 1), maxlen(x - 1, y ));
}
return dp[x][y];
}
int main()
{
int N = 0; //N 種類型的敵人和子彈
int M = 0; //M 個敵人和子彈
scanf("%d %d", &N, &M);
for (int i = 1; i <= M; i++)
{
scanf("%d", &diren[i]);
}
for (int i = 1; i <= M; i++)
{
scanf("%d", &zidan[i]);
}
for (int i = 0; i <= M; i++)
{
for (int j = 0; j <= M; j++)
dp[i][j] = 0;//為記憶化搜尋做準備
}
printf("%d", maxlen(M,M ));
system("pause");
return 0;
}
最大連續子序列和

遞推程式碼:
#include<stdio.h>
#include<stdlib.h>
const int maxn = 1000;
int a[maxn], dp[maxn];
int main()
{
int n = 0;
while (scanf("%d", &n) != EOF)
{
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
dp[i] = a[i];//初始化為本身
}
for (int i = 2; i <= n; i++)
{
dp[i] = max(dp[i - 1] + a[i], a[i]);
}
int maxsum = 0;
for (int i = 1; i <= n; i++)
{
maxsum = max(maxsum, dp[i]);
}
printf("%d\n", maxsum);
}
}遞迴程式碼:
#include<stdio.h>
#include<stdlib.h>
#include<climits>
const int maxn = 1000;
int a[maxn], dp[maxn];
int maxsum(int x)
{
if (x == 0)//遞迴出口
return 0;
if (dp[x] == INT_MIN)
return dp[x]=max(maxsum(x - 1) + a[x], a[x]);
return dp[x];
}
int main()
{
int n = 0;
while (scanf("%d", &n) != EOF)
{
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
dp[i] = INT_MIN;//有符號整型最小值
}
for (int i = 2; i <= n; i++)
{
dp[i] = maxsum(i);
}
int maxsum = 0;
for (int i = 1; i <= n; i++)
{
maxsum = max(maxsum, dp[i]);
}
printf("%d\n", maxsum);
}
system("pause");
return 0;
}相關推薦
動態規劃——線性DP.1
動態規劃演算法通常用於求解具有某種最優性質的問題。 那它和貪心有區別嗎? 當然有。不然叫動態規劃幹啥? 幼兒園英語老師:DP是啥? 小盆友:Dog&Peppa pig 英語老斯:恩恩!真聰明! 然而,你是小盆友嗎? 如果是 如果不是, DP是D
動態規劃 線性dp
動態規劃通常是用來解決最優化問題的。 一:斐波那契數列 對於斐波那契數列遞迴和非遞迴,可以參考這篇部落格:https://mp.csdn.net/postedit/79280467 如果用遞迴寫斐波那契數列,有很多重複計算值,導致時間複雜度大,可以用記憶搜
動態規劃(DP)
first 個數 目的 進入 right 返回值 ase lines cal 在學習動態規劃前 , 先補充些有關遞歸的知識 。 所謂的遞歸函數 就是調用自身函數的過程 ,因此是用棧來存儲的 。 遞歸函數的最終返回值 就是第一次調用函數的返回值 。 在寫
【Foreign】動態規劃 [分治][DP]
tex oid ans script 決策 cst pen 因此 out 動態規劃 Time Limit: 50 Sec Memory Limit: 128 MB Description 一開始有n個數,一段區間的價值為這段區間相同的數的對數。 我們想
動態規劃-樹形DP-樹上背包專題
ace 整數 return urn edge 最大 沒有 != 格式 先看道題:選課 題目描述 在大學裏每個學生,為了達到一定的學分,必須從很多課程裏選擇一些課程來學習,在課程裏有些課程必須在某些課程之前學習,如高等數學總是在其它課程之前學習。 現在有N門功課,每門課有個
初探動態規劃(DP)
isp exit min 管理 應該 一行 註意 習慣 試圖 學習qzz的命名,來寫一篇關於動態規劃(dp)的入門博客。 動態規劃應該算是一個入門oier的坑,動態規劃的抽象即神奇之處,讓很多萌新 萌比。 寫這篇博客的目標,就是想要用一些容易理解的方式,講解入門動態規劃的真
[動態規劃][樹形dp]Bichrome Tree
stream ace cat 提示 題目 inpu rmi code inf 題目描述 We have a tree with N vertices. Vertex 1 is the root of the tree, and the parent of Vertex i
[動態規劃][數位dp]不要62
號碼 每次 type 交通 main cst spa 消息 put Problem Description 杭州人稱那些傻乎乎粘嗒嗒的人為62(音:laoer)。杭州交通管理局經常會擴充一些的士車牌照,新近出來一個好消息,以後上牌照,不再含有不吉利的數字了,這樣一來,就可
[動態規劃][數位dp]Bomb
sin input them ++ counter pac sam help while Problem Description The counter-terrorists found a time bomb in the dust. But this time the
01背包問題與動態規劃(DP)
clas const 解法 自己 沒有 end ostream 初始化 動手 解法一:我們先用最樸素的方法,著眼於每個物體是否進入背包,進行遍歷。 代碼如下: #include<iostream> #include<algorithm&
[SCOI2007]壓縮(動態規劃,區間dp,字串雜湊)
[SCOI2007]壓縮 狀態:設\(dp[i][j]\)表示前i個字元,最後一個\(M\)放置在\(j\)位置之後的最短字串長度. 轉移有三類,用刷表法來實現. 第一種是直接往壓縮串後面填字元,這樣就是: \[dp[i+1][j]=min(dp[i+1][j],dp[i][j]+1)\] 另外一種
動態規劃(DP)演算法
動態規劃相信大家都知道,動態規劃演算法也是新手在剛接觸演算法設計時很苦惱的問題,有時候覺得難以理解,但是真正理解之後,就會覺得動態規劃其實並沒有想象中那麼難。網上也有很多關於講解動態規劃的文章,大多都是敘述概念,講解原理,讓人覺得晦澀難懂,即使一時
Exploring Pyramids【動態規劃——區間DP】
Exploring Pyramids UVALive - 3516 題目傳送門 題目大意:給你一個字串,其代表的是機器人來回走過的路徑,機器人總是先走左邊再走右邊,問有多少種情況。 解決方法:設輸入序列為S,d(i,j)為子序列Si,Si+1,…,Sj對應
由Leetcode詳解演算法 之 動態規劃(DP)
因為最近一段時間接觸了一些Leetcode上的題目,發現許多題目的解題思路相似,從中其實可以瞭解某類演算法的一些應用場景。 這個隨筆系列就是我嘗試的分析總結,希望也能給大家一些啟發。 動態規劃的基本概念 一言以蔽之,動態規劃就是將大問題分成小問題,以迭代的方式求解。 可以使用動態規劃求解的問題
一文弄懂動態規劃(DP Dynamic Programming)下樓梯,國王和金礦,揹包問題,Dijkstra演算法
動態規劃 參考連結 漫畫演算法,什麼是動態規劃? DP 動態規劃是一種分階段求解決策問題的數學思想 題目一 問:下樓梯問題,有一座高度是10級臺階的樓梯,從下往上走,每跨一步只能向上1級或者2級臺階,請問有多少中走法。 思路 剛才這個題目,你每走一步就有兩
演算法總結之動態規劃(DP)
適用動態規劃的特點 所解決的問題是最優化問題。 所解決的問題具有“最優子結構”。可以建立一個遞推關係,使得n階段的問題,可以通過幾個k<n階段的低階子問題的最優解來求解。 具有“重疊子結構”的特點。即,求解低階子問題時存在重複計算。 詞典法 大家都知道,遞迴演算法一般都存在大量的重複計算,這會造成不
對記憶化搜尋(ms)和動態規劃(dp)的深入理解
六月中旬了,馬上就要期末考試了,期末考試結束以後就要迎來緊張刺激的留校集訓,到那時部落格會更新的比較頻繁,而現在在準備期末考試,所以可能更新的部落格稍微少一些。 話不多說,今天來更一篇剛剛吃飯的時候關於記憶化搜尋和動態規劃的一些區別的思考。 記憶化搜尋(M
一道題看懂遞迴、(深度搜索)dfs、記憶化搜尋、動態規劃(DP)的差別!
有一個層數為n(n<=1000)的數字三角形。現有一隻螞蟻從頂層開始向下走,每走下一級,可向左下方向或右下方向走。求走到底層後它所經過數字的總和的最大值。 【輸入格式】 第一個整數為n,一下n行為各層的數字。 【輸出格式】 一個整數,即最大值。
HDU 1069.Monkey and Banana【動態規劃(DP)】【8月15】
A group of researchers are designing an experiment to test the IQ of a monkey. They will hang a banana at the roof of a building, and at the mean time, pr
演算法:動態規劃——線性模型之小朋友過橋
題目:在一個夜黑風高的晚上,有n(n <= 50)個小朋友在橋的這邊,現在他們需要過橋,但是由於橋很窄,每次只允許不大於兩人通過,他們只有一個手電筒,所以每次過橋的兩個人需要把手電筒帶回來,i號小朋友過橋的時間為T[i],兩個人過橋的總時間為二者中時間長者。問所有小朋友過橋的總時間最短是多少。