練習：建立感知

# ----------
# 
# In this exercise, you will add in code that decides whether a perceptron will fire based
# on the threshold. Your code will go in lines 32 and 34. 
#
# ----------
import numpy as np

class Perceptron:
    """
    This class models an artificial neuron with step activation function.
    """
 

    def __init__(self, weights = np.array([1]), threshold = 0):
        """
        Initialize weights and threshold based on input arguments. Note that no
        type-checking is being performed here for simplicity.
        """
        self.weights = weights
        self.threshold = threshold

    def
 
 activate(self,inputs):
        """
        Takes in @param inputs, a list of numbers equal to length of weights.
        @return the output of a threshold perceptron with given inputs based on
        perceptron weights and threshold.
        """ 

        # The strength with which the perceptron fires.
 

        strength = np.dot(self.weights, inputs)
        # TODO: return 0 or 1 based on the threshold
        if strength <= self.threshold :
            self.result = 0# TODO
        else:
            self.result = 1# TODO    
        return self.result


def test():
    """
    A few tests to make sure that the perceptron class performs as expected.
    Nothing should show up in the output if all the assertions pass.
    """
    p1 = Perceptron(np.array([1, 2]), 0.)
    assert p1.activate(np.array([ 1,-1])) == 0 # < threshold --> 0
    assert p1.activate(np.array([-1, 1])) == 1 # > threshold --> 1
    assert p1.activate(np.array([ 2,-1])) == 0 # on threshold --> 0

if __name__ == "__main__":
    test()

練習：在哪兒訓練感知

權重

練習：感知輸入

每行帶有標籤的數值型矩陣

練習：神經網路輸出

• 一個有向圖
• 一個標量
• 用向量表示的分類資訊
• 每個輸入向量都對應一個輸出向量

練習：感知更新規則

# ----------
#
# In this exercise, you will update the perceptron class so that it can update
# its weights.
#
# Finish writing the update() method so that it updates the weights according
# to the perceptron update rule. Updates should be performed online, revising
# the weights after each data point.
#
# YOUR CODE WILL GO IN LINES 51 AND 59.
# ----------

import numpy as np

class Perceptron:
    """
    This class models an artificial neuron with step activation function.
    """
    def __init__(self, weights = np.array([1]), threshold = 0):
        """
        Initialize weights and threshold based on input arguments. Note that no
        type-checking is being performed here for simplicity.
        """
        self.weights = weights.astype(float) 
        self.threshold = threshold


    def activate(self, values):
        """
        Takes in @param values, a list of numbers equal to length of weights.
        @return the output of a threshold perceptron with given inputs based on
        perceptron weights and threshold.
        """
        # First calculate the strength with which the perceptron fires
        strength = np.dot(values,self.weights)
        # Then return 0 or 1 depending on strength compared to threshold  
        return int(strength > self.threshold)


    def update(self, values, train, eta=.1):
        """
        Takes in a 2D array @param values consisting of a LIST of inputs and a
        1D array @param train, consisting of a corresponding list of expected
        outputs. Updates internal weights according to the perceptron training
        rule using these values and an optional learning rate, @param eta.
        """

        # For each data point:
        for data_point in xrange(len(values)):
            # TODO: Obtain the neuron's prediction for the data_point --> values[data_point]
            prediction = self.activate(values[data_point])
            # Get the prediction accuracy calculated as (expected value - predicted value)
            # expected value = train[data_point], predicted value = prediction
            error = train[data_point] - prediction
            # TODO: update self.weights based on the multiplication of:
            # - prediction accuracy(error)
            # - learning rate(eta)
            # - input value(values[data_point])
            weight_update =  eta*error*values[data_point]
            self.weights += weight_update

def test():
    """
    A few tests to make sure that the perceptron class performs as expected.
    Nothing should show up in the output if all the assertions pass.
    """
    def sum_almost_equal(array1, array2, tol = 1e-6):
        return sum(abs(array1 - array2)) < tol

    p1 = Perceptron(np.array([1,1,1]),0)
    p1.update(np.array([[2,0,-3]]), np.array([1]))
    assert sum_almost_equal(p1.weights, np.array([1.2, 1, 0.7]))

    p2 = Perceptron(np.array([1,2,3]),0)
    p2.update(np.array([[3,2,1],[4,0,-1]]),np.array([0,0]))
    assert sum_almost_equal(p2.weights, np.array([0.7, 1.8, 2.9]))

    p3 = Perceptron(np.array([3,0,2]),0)
    p3.update(np.array([[2,-2,4],[-1,-3,2],[0,2,1]]),np.array([0,1,0]))
    assert sum_almost_equal(p3.weights, np.array([2.7, -0.3, 1.7]))

if __name__ == "__main__":
    test()

練習：多層網路示例

• answer:-25

import numpy as np

X = np.array([1, 2, 3])
weight_hidden = np.array([[1, 1, -5], [3, -4, 2]]).transpose()
weight_output = np.array([[2, -1]]).transpose()

X_hidden = np.dot(X, weight_hidden)
X_output = np.dot(X_hidden, weight_output)

print("{}".format(X_output))

練習：線性表正能力

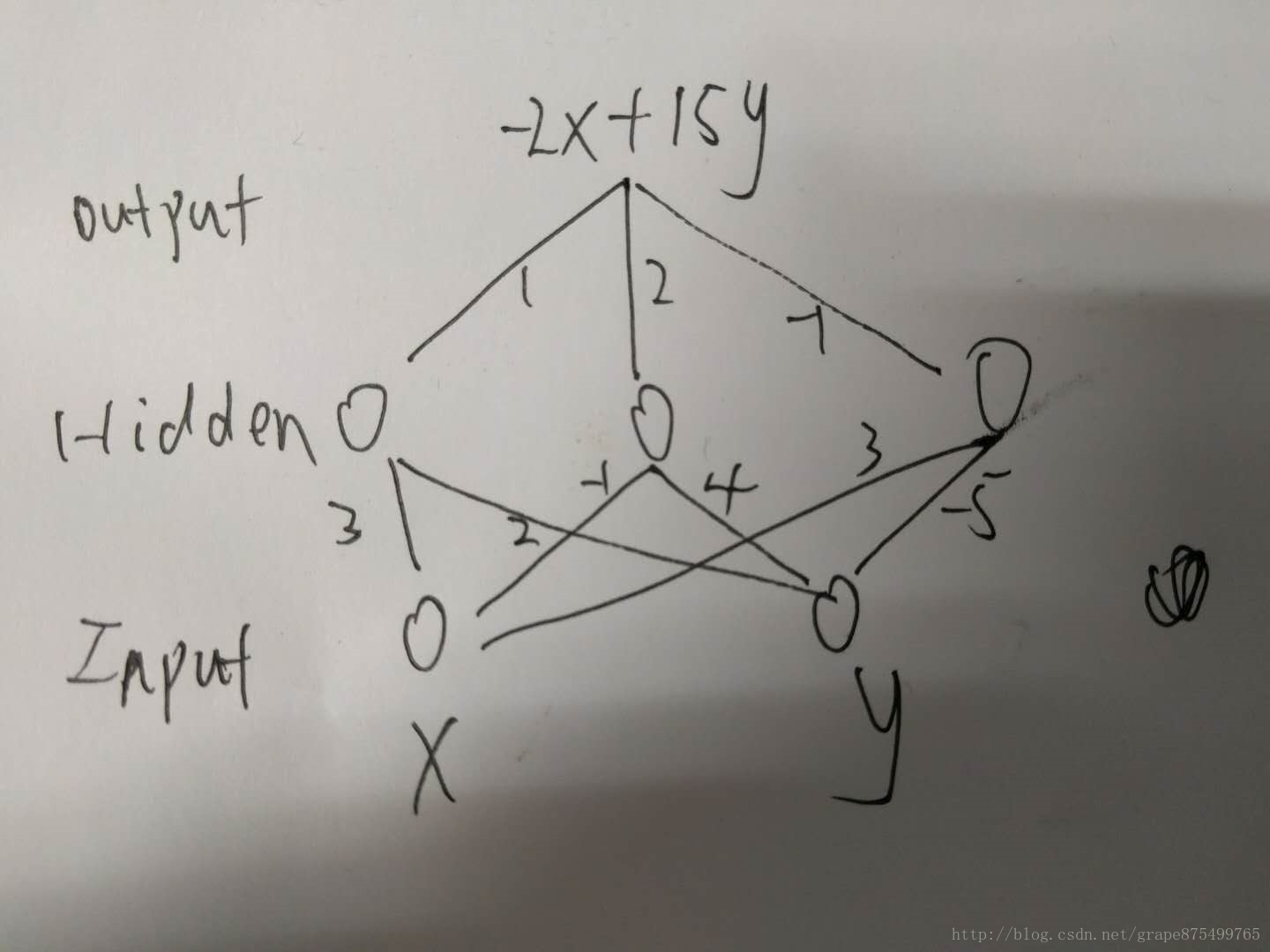
圖來自Udacity論壇

練習：建立XOR網路

下面的演算法依據上圖建立

# ----------
#
# In this exercise, you will create a network of perceptrons that can represent
# the XOR function, using a network structure like those shown in the previous
# quizzes.
#
# You will need to do two things:
# First, create a network of perceptrons with the correct weights
# Second, define a procedure EvalNetwork() which takes in a list of inputs and
# outputs the value of this network.
#
# ----------

import numpy as np

class Perceptron:
    """
    This class models an artificial neuron with step activation function.
    """

    def __init__(self, weights = np.array([1]), threshold = 0):
        """
        Initialize weights and threshold based on input arguments. Note that no
        type-checking is being performed here for simplicity.
        """
        self.weights = weights
        self.threshold = threshold


    def activate(self, values):
        """
        Takes in @param values, a list of numbers equal to length of weights.
        @return the output of a threshold perceptron with given inputs based on
        perceptron weights and threshold.
        """

        # First calculate the strength with which the perceptron fires
        strength = np.dot(values,self.weights)

        # Then return 0 or 1 depending on strength compared to threshold  
        return int(strength > self.threshold)


# Part 1: Set up the perceptron network
Network = [
    # input layer, declare input layer perceptrons here
    [ Perceptron(np.array([1,1]),0.5),Perceptron(np.array([-1,-1]),-1.5) ], \
    # output node, declare output layer perceptron here
    [ Perceptron(np.array([1,1]),1.5) ]
]

# Part 2: Define a procedure to compute the output of the network, given inputs
def EvalNetwork(inputValues, Network):
    """
    Takes in @param inputValues, a list of input values, and @param Network
    that specifies a perceptron network. @return the output of the Network for
    the given set of inputs.
    """

    # YOUR CODE HERE
    p1 = Network[0][0].activate(inputValues)
    p2 = Network[0][1].activate(inputValues)
    OutputValue = Network[1][0].activate(np.array([p1,p2]))
    # Be sure your output value is a single number
    return OutputValue


def test():
    """
    A few tests to make sure that the perceptron class performs as expected.
    """
    print "0 XOR 0 = 0?:", EvalNetwork(np.array([0,0]), Network)
    print "0 XOR 1 = 1?:", EvalNetwork(np.array([0,1]), Network)
    print "1 XOR 0 = 1?:", EvalNetwork(np.array([1,0]), Network)
    print "1 XOR 1 = 0?:", EvalNetwork(np.array([1,1]), Network)

if __name__ == "__main__":
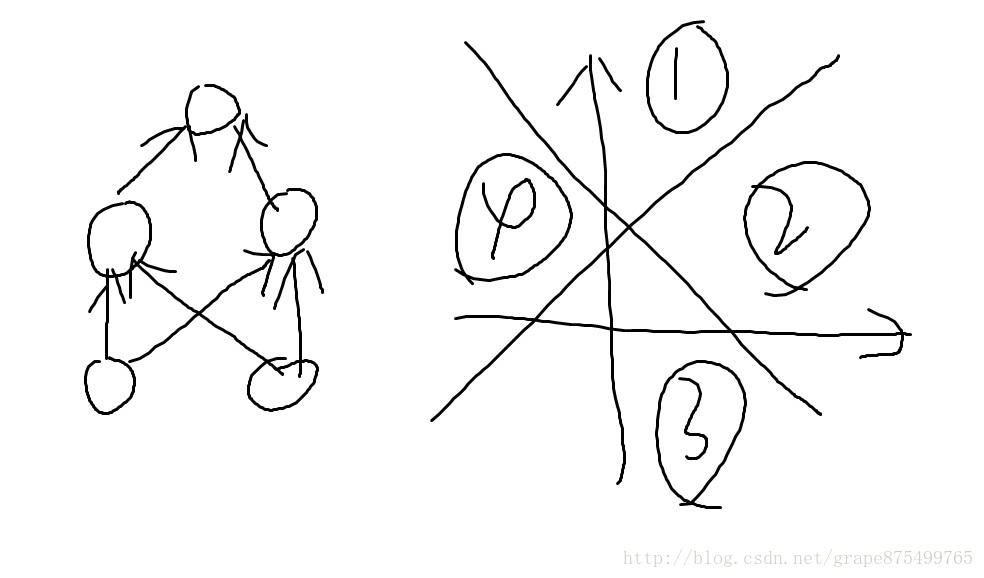
    test()

練習：離散測驗

• answer:4

類似XOR結構，最多有四種輸出情況，分類區域會出現交叉線，進而分出了四塊區域，也就是四個分類

練習：啟用函式沙盒

# ----------
# 
# Python Neural Networks code originally by Szabo Roland and used with
# permission
#
# Modifications, comments, and exercise breakdowns by Mitchell Owen,
# (c) Udacity
#
# Retrieved originally from http://rolisz.ro/2013/04/18/neural-networks-in-python/
#
#
# Neural Network Sandbox
#
# Define an activation function activate(), which takes in a number and
# returns a number.
# Using test run you can see the performance of a neural network running with
# that activation function, where the inputs are 8x8 images of digits (0-9) and
# the outputs are digit predictions made by the network.
#
# ----------

import numpy as np


def activate(strength):
    # Try out different functions here. Input strength will be a number, with
    # another number as output.
    return np.power(strength,2)

def activation_derivative(activate, strength):
    #numerically approximate
    return (activate(strength+1e-5)-activate(strength-1e-5))/(2e-5)

練習：啟用函式 測驗

• Logistic function

練習：感知 v.s. Sigmoid

• 後者給出了更多的資訊，但是兩者的結果會相同

練習：Sigmoid學習

• 運用微積分

練習：梯度下降問題

• 區域性的極值
• 執行太耗時
• 會產生無限次迴圈
• 無法收斂

練習：Sigmoid 程式設計練習

# ----------
# 
# As with the previous perceptron exercises, you will complete some of the core
# methods of a sigmoid unit class.
#
# There are two functions for you to finish:
# First, in activate(), write the sigmoid activation function.
# Second, in update(), write the gradient descent update rule. Updates should be
#   performed online, revising the weights after each data point.
# 
# ----------

import numpy as np


class Sigmoid:
    """
    This class models an artificial neuron with sigmoid activation function.
    """

    def __init__(self, weights = np.array([1])):
        """
        Initialize weights based on input arguments. Note that no type-checking
        is being performed here for simplicity of code.
        """
        self.weights = weights

        # NOTE: You do not need to worry about these two attribues for this
        # programming quiz, but these will be useful for if you want to create
        # a network out of these sigmoid units!
        self.last_input = 0 # strength of last input
        self.delta      = 0 # error signal

    def activate(self, values):
        """
        Takes in @param values, a list of numbers equal to length of weights.
        @return the output of a sigmoid unit with given inputs based on unit
        weights.
        """

        # YOUR CODE HERE

        # First calculate the strength of the input signal.
        strength = np.dot(values, self.weights)
        self.last_input = strength

        result = self.logistic(strength)
        # TODO: Modify strength using the sigmoid activation function and
        # return as output signal.
        # HINT: You may want to create a helper function to compute the
        #   logistic function since you will need it for the update function.

        return result

    def logistic(self, X):  
        return 1.0/(1+np.exp(-X))

    def update(self, values, train, eta=.1):
        """
        Takes in a 2D array @param values consisting of a LIST of inputs and a
        1D array @param train, consisting of a corresponding list of expected
        outputs. Updates internal weights according to gradient descent using
        these values and an optional learning rate, @param eta.
        """

        # TODO: for each data point...
        for X, y_true in zip(values, train):
            # obtain the output signal for that point
            y_pred = self.activate(X)

            # YOUR CODE HERE
            error = y_true - y_pred
            # TODO: compute derivative of logistic function at input strength
            # Recall: d/dx logistic(x) = logistic(x)*(1-logistic(x))
            dx = self.logistic(self.last_input) * (1-self.logistic(self.last_input))
            # TODO: update self.weights based on learning rate, signal accuracy,
            # function slope (derivative) and input value
            weight_update =  eta*dx*error*X
            self.weights += weight_update



def test():
    """
    A few tests to make sure that the perceptron class performs as expected.
    Nothing should show up in the output if all the assertions pass.
    """
    def sum_almost_equal(array1, array2, tol = 1e-5):
        return sum(abs(array1 - array2)) < tol

    u1 = Sigmoid(weights=[3,-2,1])
    assert abs(u1.activate(np.array([1,2,3])) - 0.880797) < 1e-5

    u1.update(np.array([[1,2,3]]),np.array([0]))
    assert sum_almost_equal(u1.weights, np.array([2.990752, -2.018496, 0.972257]))

    u2 = Sigmoid(weights=[0,3,-1])
    u2.update(np.array([[-3,-1,2],[2,1,2]]),np.array([1,0]))
    assert sum_almost_equal(u2.weights, np.array([-0.030739, 2.984961, -1.027437]))

if __name__ == "__main__":
    test()