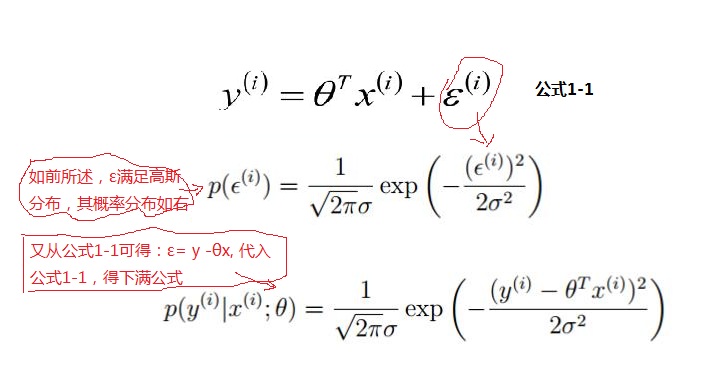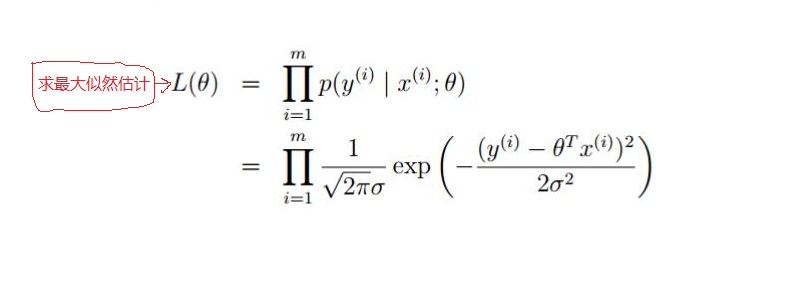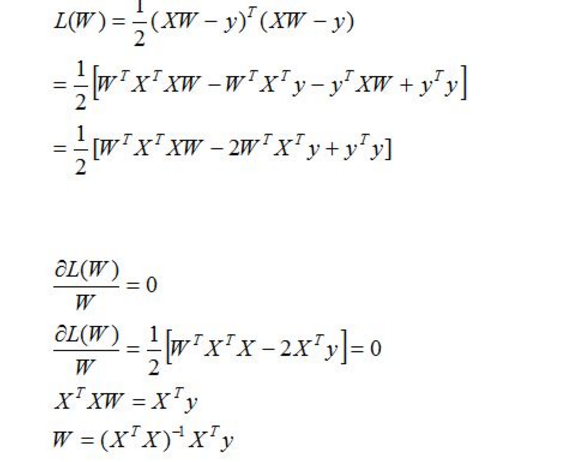用矩陣方式求解線性回歸的最優θ
阿新 • • 發佈:2019-01-16
資料 假設 blog cnblogs 方程 一定的 alt http 出了
1.假設回歸的目標函數式為

(其中x0為1)
當 n = 1時表示一元函數,對一元函數進行回歸分析
2.將誤差記為:ε

要使得ε最小,然後樣本真實值 y 和模型訓練預測的值之間是有誤差 ε ,再假設訓練樣本的數據量很大的時候,根據中心極限定律可以得到 ∑ε 滿足 (u ,δ2)高斯分布的;由於方程有截距項 ,故使用可以 u =0; 故滿足(0,δ2)的高斯分布;
如上面可知,對於每一個樣本 x ,代入到 p (y |x ;θ) 都會得到一個y 的概率;又因為設定樣本是獨立同分布的;對其求最大似然函數:
對其化簡如下:
對目標求解求偏導
以上就得到了回歸的損失函數最小二乘法的公式,對於好多介紹一般對線性回歸的線性損失函數就直接給出了上面的公式二乘法。下面我們就對上面做了階段性的總結:線性回歸,根據大數定律和中心極限定律假定樣本無窮大的時候,其真實值和預測值的誤差ε 的加和服從u=0,方差=δ2的高斯分布且獨立同分布,然後把ε =y-?x 代入公式,就可以化簡得到線性回歸的損失函數;
第二步:對損失函數進行優化也就是求出w,b,使的損失函數最小化;第一種方法使用矩陣(需要滿足可逆條件)
以上就是按矩陣方法優化損失函數,但上面方法有一定的局限性,就是要可逆;下面我們來說一說另外一個優化方法 梯度下降法;對於梯度下降法的說明和講解資料很多,深入的講解這裏不進行,可以參考:http://www.cnblogs.com/ooon/p/4947688.html這篇博客,博主對梯度下降方法進行了講解,我們這裏就簡單的最了流程解說;
W就是所求的參數θ矩陣。
用矩陣方式求解線性回歸的最優θ