rovio是一個緊耦合，基於影象塊的濾波實現的VIO。

他的優點是：計算量小(EKF，稀疏的影象塊)，但是對應不同的裝置需要調引數，引數對精度很重要。沒有閉環，沒有mapping thread。經常存在誤差會殘留到下一時刻。

我試了一些裝置，要是精度在幾十釐米，裝置運動不快的，一般攝像頭加一般imu，不是硬體同步就是正常的rostopic 釋出的時間，也能達到。

程式碼主要分為EKF實現的部分，和演算法相關的部分，EKF是作者自己寫的一個框架。先分析EKF程式碼

lightweight_filtering

FilterBase.hpp

template<typename Meas>
class MeasurementTimeline{
  typedef Meas mtMeas;
 //imu測量的資料存在map中，相當於一個buffer,key是時間，value 是加速度或者角速度或者影象金字塔
  std::map<double,mtMeas> measMap_;

void addMeas(const mtMeas& meas,const double &t);

}
 

EKF的整個流程框架

template<typename Prediction,typename... Updates>
class FilterBase: public PropertyHandler{
//imu和影象的兩個MeasurementTimeline
    MeasurementTimeline<typename mtPrediction::mtMeas> predictionTimeline_;
    std::tuple<MeasurementTimeline<typename Updates::mtMeas>...> updateTimelineTuple_;

//加入imu測量值
    void addPredictionMeas(const typename Prediction::mtMeas& meas, double t){
        if(t<= safeWarningTime_) {
            std::cout << "[FilterBase::addPredictionMeas] Warning: included measurements at time " << t << " before safeTime " << safeWarningTime_ << std::endl;
        }

        if(t<= frontWarningTime_) gotFrontWarning_ = true;
        predictionTimeline_.addMeas(meas,t);
    }

//影象的MeasurementTimeline
    template<int i>
    void addUpdateMeas(const typename std::tuple_element<i,decltype(mUpdates_)>::type::mtMeas& meas, double t){
        if(t<= safeWarningTime_) {
            std::cout << "[FilterBase::addUpdateMeas] Warning: included measurements at time " << t << " before safeTime " << safeWarningTime_ << std::endl;
        }
        if(t<= frontWarningTime_) gotFrontWarning_ = true;
        std::get<i>(updateTimelineTuple_).addMeas(meas,t);
    }

//根據傳入時間進行EKF的更新
    void updateSafe(const double *maxTime =  nullptr){
        //根據最新的imu測量時間，得到最近的影象測量的時間，nextSafeTime返回的是最新的影象測量時間
        bool gotSafeTime = getSafeTime(nextSafeTime);

        update(safe_,nextSafeTime);
        //清楚safetime之前的資料，但是至少留下一個測量量
        clean(safe_.t_);

    }

    void update(mtFilterState& filterState,const double& tEnd){
        while(filterState.t_ < tEnd){
            tNext = tEnd;
            //要是上一次更新之後，沒有新的影象來到，就不要更新了
            if(!getNextUpdate(filterState.t_,tNext) && updateToUpdateMeasOnly_){
                break; // Don't go further if there is no update available
            }
            int r = 0;

            //引數usePredictionMerge_是不是設定，對應的是EKF中的預測方程的f(x)設定的不一樣，看程式碼就知道
            if(filterState.usePredictionMerge_){
                r = mPrediction_.predictMerged(filterState,tNext,predictionTimeline_.measMap_);
                if(r!=0) std::cout << "Error during predictMerged: " << r << std::endl;
                logCountMerPre_++;
            } else {
                while(filterState.t_ < tNext && (predictionTimeline_.itMeas_ = predictionTimeline_.measMap_.upper_bound(filterState.t_)) != predictionTimeline_.measMap_.end()){
                    r = mPrediction_.performPrediction(filterState,predictionTimeline_.itMeas_->second,std::min(predictionTimeline_.itMeas_->first,tNext)-filterState.t_);
                    if(r!=0) std::cout << "Error during performPrediction: " << r << std::endl;
                    logCountRegPre_++;
                }
            }
            // imu和影象的時間戳不是對齊的，存在偏差，這一段時間的imu也要做EKF預測
            if(filterState.t_ < tNext){
                r = mPrediction_.performPrediction(filterState,tNext-filterState.t_);
                if(r!=0) std::cout << "Error during performPrediction: " << r << std::endl;
                logCountBadPre_++;
            }
            //　影象的更新
            doAvailableUpdates(filterState,tNext);
        }
    }

}
 

Prediction.hpp

int predictMerged(mtFilterState& filterState, double tTarget,const std::map<double, mtMeas>& measMap) {
    switch (filterState.mode_) {
    case ModeEKF:
        return predictMergedEKF(filterState, tTarget, measMap);
    case ModeUKF:
        return predictMergedUKF(filterState, tTarget, measMap);
    case ModeIEKF:
        return predictMergedEKF(filterState, tTarget, measMap);
    default:
        return predictMergedEKF(filterState, tTarget, measMap);
    }
}

virtual int predictMergedEKF(mtFilterState& filterState,const double tTarget, const std::map<double, mtMeas>& measMap)
{
    const typename std::map<double, mtMeas>::const_iterator itMeasStart = measMap.upper_bound(filterState.t_);
    if (itMeasStart == measMap.end())
        return 0;

    typename std::map<double, mtMeas>::const_iterator itMeasEnd = measMap.lower_bound(tTarget);

    if (itMeasEnd != measMap.end())
        ++itMeasEnd;

    double dT = std::min(std::prev(itMeasEnd)->first, tTarget) - filterState.t_;
    if (dT <= 0)
        return 0;

    // Compute mean Measurement
    mtMeas meanMeas;
    typename mtMeas::mtDifVec vec;
    typename mtMeas::mtDifVec difVec;
    vec.setZero();
    double t = itMeasStart->first;
    for (typename std::map<double, mtMeas>::const_iterator itMeas = next(itMeasStart);
                itMeas != itMeasEnd; itMeas++) {
        itMeasStart->second.boxMinus(itMeas->second, difVec);
    //這個是應該是減的
        vec = vec - difVec * (std::min(itMeas->first, tTarget) - t);
        t = std::min(itMeas->first, tTarget);
    }
    vec = vec / dT;
    //得到這段時間的imu平均測量
    itMeasStart->second.boxPlus(vec, meanMeas);

    preProcess(filterState, meanMeas, dT);
    meas_ = meanMeas;
    //雅可比矩陣的求解
    this->jacPreviousState(filterState.F_, filterState.state_, dT);
    this->jacNoise(filterState.G_, filterState.state_, dT); // Works for time continuous parametrization of noise

    for (typename std::map<double, mtMeas>::const_iterator itMeas =
            itMeasStart; itMeas != itMeasEnd; itMeas++) {
        meas_ = itMeas->second;
        this->evalPredictionShort(filterState.state_, filterState.state_,
                std::min(itMeas->first, tTarget) - filterState.t_);
        filterState.t_ = std::min(itMeas->first, tTarget);
    }
    filterState.cov_ = filterState.F_ * filterState.cov_
            * filterState.F_.transpose()
            + filterState.G_ * prenoiP_ * filterState.G_.transpose();
    filterState.state_.fix();
    enforceSymmetry(filterState.cov_);

    filterState.t_ = std::min(std::prev(itMeasEnd)->first, tTarget);
    postProcess(filterState, meanMeas, dT);
    return 0;
}
 

update.hpp

int performUpdateEKF(mtFilterState& filterState, const mtMeas& meas) {
    meas_ = meas;
    if (!useSpecialLinearizationPoint_) {
        this->jacState(H_, filterState.state_);
        Hlin_ = H_;
        this->jacNoise(Hn_, filterState.state_);
        this->evalInnovationShort(y_, filterState.state_);
    } else {
        filterState.state_.boxPlus(filterState.difVecLin_, linState_);
        this->jacState(H_, linState_);
        if (useImprovedJacobian_) {
            filterState.state_.boxMinusJac(linState_, boxMinusJac_);
            Hlin_ = H_ * boxMinusJac_;
        } else {
            Hlin_ = H_;
        }
        this->jacNoise(Hn_, linState_);
        this->evalInnovationShort(y_, linState_);
    }

    if (isCoupled) {
        C_ = filterState.G_ * preupdnoiP_ * Hn_.transpose();
        Py_ = Hlin_ * filterState.cov_ * Hlin_.transpose()
                + Hn_ * updnoiP_ * Hn_.transpose() + Hlin_ * C_
                + C_.transpose() * Hlin_.transpose();
    } else {
        Py_ = Hlin_ * filterState.cov_ * Hlin_.transpose() + Hn_ * updnoiP_ * Hn_.transpose();
    }
    y_.boxMinus(yIdentity_, innVector_);

    // Outlier detection // TODO: adapt for special linearization point
    //根據方差和residual的乘積是否超多閥值判斷outlier
    outlierDetection_.doOutlierDetection(innVector_, Py_, Hlin_);
    Pyinv_.setIdentity();
    Py_.llt().solveInPlace(Pyinv_);

    if(outlierDetection_.isOutlier(0)){
        LOG(INFO) << "innovation vector: " << innVector_(0) << " , " << innVector_(1);
//          LOG(INFO) << "covariance :\n " << Py_.block(0,0,2,2);
    }

    // Kalman Update
    if (isCoupled) {
        K_ = (filterState.cov_ * Hlin_.transpose() + C_) * Pyinv_;
    } else {
        K_ = filterState.cov_ * Hlin_.transpose() * Pyinv_;
    }
    filterState.cov_ = filterState.cov_ - K_ * Py_ * K_.transpose();
    if (!useSpecialLinearizationPoint_) {
        updateVec_ = -K_ * innVector_;
    } else {
        filterState.state_.boxMinus(linState_, difVecLinInv_);
        updateVec_ = -K_ * (innVector_ + H_ * difVecLinInv_); // includes correction for offseted linearization point, dif must be recomputed (a-b != (-(b-a)))
    }
    filterState.state_.boxPlus(updateVec_, filterState.state_);

//      LOG(INFO) << "updateVec pos vel:\n " << updateVec_.block(0,0,6,1).transpose();
    return 0;
}

State.hpp

旋轉量使用四元數表示是4個自由度，但是旋轉只要3個自由度表示，要用李代數表示。

這個是bearing vector的引數表示方式。在tangent space 中表示，這部分我只理解部分。具體的可以參考作者的博士論文，最後一章。

class NormalVectorElement: public ElementBase<NormalVectorElement,NormalVectorElement,2>{
public:

QPD q_;

NormalVectorElement(const V3D& vec): e_x(1,0,0), e_y(0,1,0), e_z(0,0,1){
    setFromVector(vec);  //就是vec和e_z之間的旋轉變換
}

void setFromVector(V3D vec){
    const double d = vec.norm();
    if(d > 1e-6){
      vec = vec/d;
      q_ = q_.exponentialMap(getRotationFromTwoNormals(e_z,vec,e_x));
    } else {
      q_.setIdentity();
    }
}

//　ｚ軸跟bearing vector之間的旋轉變換
static V3D getRotationFromTwoNormals(const V3D& a, const V3D& b, const V3D& a_perp) {
    const V3D cross = a.cross(b);
    const double crossNorm = cross.norm();
    const double c = a.dot(b);
    const double angle = std::acos(c);
    if (crossNorm < 1e-6) {
        //0度
        if (c > 0) {
            return cross;
        } else {//180 度
            return a_perp * M_PI;
        }
    } else {//\theta a  旋轉軸＋旋轉角的表示
        return cross * (angle / crossNorm);
    }
}

V3D getVec() const{
    return q_.rotate(e_z);
}

V3D getPerp1() const{
    return q_.rotate(e_x);
}
V3D getPerp2() const{
    return q_.rotate(e_y);
}

Eigen::Matrix<double,3,2> getN() const {
    Eigen::Matrix<double,3,2> M;
    M.col(0) = getPerp1();
    M.col(1) = getPerp2();
    return M;
}

}

rovio

博士論文

博士論文的最後一章對演算法的bearing vector的公式詳細的推導了。

這部分主要是演算法的部分。

RovioNode.hpp

template<typename FILTER>
class RovioNode{

struct FilterInitializationState {
    FilterInitializationState()
        : WrWM_(V3D::Zero()),
        //使用加速度進行初始化的方向確定
            state_(State::WaitForInitUsingAccel) {}
};

void imuCallback(const sensor_msgs::Imu::ConstPtr& imu_msg){
    std::lock_guard<std::mutex> lock(m_filter_);
    predictionMeas_.template get<mtPredictionMeas::_acc>() = Eigen::Vector3d(imu_msg->linear_acceleration.x,imu_msg->linear_acceleration.y,imu_msg->linear_acceleration.z);

    predictionMeas_.template get<mtPredictionMeas::_gyr>() = Eigen::Vector3d(imu_msg->angular_velocity.x,imu_msg->angular_velocity.y,imu_msg->angular_velocity.z);
    
    if(init_state_.isInitialized()){
        //
        mpFilter_->addPredictionMeas(predictionMeas_,imu_msg->header.stamp.toSec());
        updateAndPublish();
    } else {
        switch(init_state_.state_) {
            case FilterInitializationState::State::WaitForInitExternalPose: {
                std::cout << "-- Filter: Initializing using external pose ..." << std::endl;
                mpFilter_->resetWithPose(init_state_.WrWM_, init_state_.qMW_, imu_msg->header.stamp.toSec());
                break;
            }
            case FilterInitializationState::State::WaitForInitUsingAccel: {
                std::cout << "-- Filter: Initializing using accel. measurement ..." << std::endl;
                mpFilter_->resetWithAccelerometer(predictionMeas_.template get<mtPredictionMeas::_acc>(),imu_msg->header.stamp.toSec());
                break;
            }
            default: {
                std::cout << "Unhandeld initialization type." << std::endl;
                abort();
                break;
            }
        }

        std::cout << std::setprecision(12);
        std::cout << "-- Filter: Initialized at t = " << imu_msg->header.stamp.toSec() << std::endl;
        init_state_.state_ = FilterInitializationState::State::Initialized;
    }
}

void imgCallback(const sensor_msgs::ImageConstPtr & img, const int camID = 0){
// Get image from msg
  cv_bridge::CvImagePtr cv_ptr;
  try {
      cv_ptr = cv_bridge::toCvCopy(img, sensor_msgs::image_encodings::TYPE_8UC1);
  } catch (cv_bridge::Exception& e) {
      ROS_ERROR("cv_bridge exception: %s", e.what());
      return;
  }
  cv::Mat cv_img;
  cv_ptr->image.copyTo(cv_img);
  if(init_state_.isInitialized() && !cv_img.empty()){
      double msgTime = img->header.stamp.toSec();
      if(msgTime != imgUpdateMeas_.template get<mtImgMeas::_aux>().imgTime_){
          for(int i=0;i<mtState::nCam_;i++){
              if(imgUpdateMeas_.template get<mtImgMeas::_aux>().isValidPyr_[i]){
                  std::cout << "    \033[31mFailed Synchronization of Camera Frames, t = " << msgTime << "\033[0m" << std::endl;
              }
          }
          imgUpdateMeas_.template get<mtImgMeas::_aux>().reset(msgTime);
      }
      imgUpdateMeas_.template get<mtImgMeas::_aux>().pyr_[camID].computeFromImage(cv_img,true);
      imgUpdateMeas_.template get<mtImgMeas::_aux>().isValidPyr_[camID] = true;

      if(imgUpdateMeas_.template get<mtImgMeas::_aux>().areAllValid()){
          mpFilter_->template addUpdateMeas<0>(imgUpdateMeas_,msgTime);
          imgUpdateMeas_.template get<mtImgMeas::_aux>().reset(msgTime);
          updateAndPublish();
      }
  }
}

}

ImuPrediction.hpp

公式的推導可以參考的論文，

\[ \begin{equation} \sideset{_I\,}{_{IB}}{\overline r} = \sideset{_I\,}{_{IB}}r + \Delta t \Phi _{IB}(\sideset {_B\,}{_B}{v} + \sideset{_B\,}{_v}{n}) \label{eq:position} \end{equation} \]

\[ \begin{equation} \sideset {_B\,}{_B}{ \overline v} = \sideset {_B\,}{_B}{v} + \Delta t (\Phi {_{IB}^{-1}} (g) + f - {w^{\times}}_{B}v_{B}) \label{eq:velocity} \end{equation} \]

\[ \begin{equation} {\overline \Phi} _{IB} = \Phi _{IB} \circ exp(\Delta t \omega) \label{eq:orientation} \end{equation} \]

\[ \begin{equation} \sideset {_B\,}{_f}{\overline b} = \sideset {_B\,}{_f}b + \Delta t \sideset{_B \,}{_{bf}} n \label{eq:noise1} \end{equation} \]

\[ \begin{equation} \sideset {_B\,}{_ \omega}{\overline b} = \sideset {_B\,}{_ \omega}b + \Delta t \sideset{_B \,}{_{b\omega}} n \label{eq:noise2} \end{equation} \]

\[ \begin{equation} {\mu _{i}}' = N^T(\mu _{i}) \hat {\omega} _{v} - \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} N^T(\mu _i) \frac{\hat v_{v}}{d (\rho _i)} + \omega _{\mu , i} \text{ , bearing vector} \label{eq:bearingVector} \end{equation} \]

\[ \begin{equation} {\rho _i}' = \frac{d \rho}{dt} = \frac{d \rho}{d d} \frac{d d}{dt} = \frac{ -\mu_i^T \hat{v_v}}{d'(\rho _i)} + \omega_{\rho,i} \text{, inverse distance} \label{eq:inversedistance} \end{equation} \]

template<typename FILTERSTATE>
class ImuPrediction: public LWF::Prediction<FILTERSTATE>{
{
    void evalPrediction(mtState& output, const mtState& state, const mtNoise& noise, double dt) const
    {
        output.aux().MwWMmeas_ = meas_.template get<mtMeas::_gyr>();
        output.aux().MwWMest_  = meas_.template get<mtMeas::_gyr>()-state.gyb();
        const V3D imuRor = output.aux().MwWMest_+noise.template get<mtNoise::_att>()/sqrt(dt);
        const V3D dOmega = dt*imuRor;
        QPD dQ = dQ.exponentialMap(dOmega);

        for(unsigned int i=0;i<mtState::nMax_;i++){
            const int camID = state.CfP(i).camID_;
            if(&output != &state){
                output.CfP(i) = state.CfP(i);
                output.dep(i) = state.dep(i);
            }
            if(camID >= 0 && camID < mtState::nCam_){
                //cam的角速度，在camera 座標系
                const V3D camRor = state.qCM(camID).rotate(imuRor);
                //這裡的速度取了負號,camera　速度，在camera　座標系
                const V3D camVel = state.qCM(camID).rotate(V3D(imuRor.cross(state.MrMC(camID))-state.MvM()));

                oldC_ = state.CfP(i);
                oldD_ = state.dep(i);
                //公式７的離散公式，一階積分
                output.dep(i).p_ = oldD_.p_-dt*oldD_.getParameterDerivative()*oldC_.get_nor().getVec().transpose()*camVel + noise.template get<mtNoise::_fea>(i)(2)*sqrt(dt);

                V3D dm = -dt*(gSM(oldC_.get_nor().getVec())*camVel/oldD_.getDistance()
                  + (M3D::Identity()-oldC_.get_nor().getVec()*oldC_.get_nor().getVec().transpose())*camRor)
                + oldC_.get_nor().getN()*noise.template get<mtNoise::_fea>(i).template block<2,1>(0,0)*sqrt(dt);
                
                QPD qm = qm.exponentialMap(dm);
                output.CfP(i).set_nor(oldC_.get_nor().rotated(qm));

        // WARP corners
                if(state.CfP(i).trackWarping_){
                    bearingVectorJac_ = output.CfP(i).get_nor().getM().transpose()*(dt*gSM(qm.rotate(oldC_.get_nor().getVec()))*Lmat(dm)*(
                          -1.0/oldD_.getDistance()*gSM(camVel)
                          - (M3D::Identity()*(oldC_.get_nor().getVec().dot(camRor))+oldC_.get_nor().getVec()*camRor.transpose()))
                      +MPD(qm).matrix())*oldC_.get_nor().getM();
                    output.CfP(i).set_warp_nor(bearingVectorJac_*oldC_.get_warp_nor());
                }
            }
        }
        //　上面的1-5公式
        output.WrWM() = state.WrWM()-dt*(state.qWM().rotate(state.MvM())-noise.template get<mtNoise::_pos>()/sqrt(dt));
        output.MvM() = (M3D::Identity()-gSM(dOmega))*state.MvM()-dt*(meas_.template get<mtMeas::_acc>()-state.acb()+state.qWM().inverseRotate(g_)-noise.template get<mtNoise::_vel>()/sqrt(dt));
        output.acb() = state.acb()+noise.template get<mtNoise::_acb>()*sqrt(dt);
        output.gyb() = state.gyb()+noise.template get<mtNoise::_gyb>()*sqrt(dt);
        output.qWM() = state.qWM()*dQ;

        //camera 和imu 的外引數
        for(unsigned int i=0;i<mtState::nCam_;i++){
            output.MrMC(i) = state.MrMC(i)+noise.template get<mtNoise::_vep>(i)*sqrt(dt);
            dQ = dQ.exponentialMap(noise.template get<mtNoise::_vea>(i)*sqrt(dt));
            output.qCM(i) = state.qCM(i)*dQ;    
        }


        output.aux().wMeasCov_ = prenoiP_.template block<3,3>(mtNoise::template getId<mtNoise::_att>(),mtNoise::template getId<mtNoise::_att>())/dt;
        output.fix();

    }
}

ImgUpdate.hpp

• Stack all photometric error terms into a vector b, you get b(p)
• Linearize the error around \(\hat{p}\), you get \(b(dp) = b(\hat{p}) + A(\hat{p}) dp\)
• Set it to zero and solve for dp, you get the equation $-b(\hat{p}) = A(\hat{p}) dp $

template<typename FILTERSTATE>
class ImgUpdate: public LWF::Update<ImgInnovation<typename FILTERSTATE::mtState>,FILTERSTATE,ImgUpdateMeas<typename FILTERSTATE::mtState>,ImgUpdateNoise<typename FILTERSTATE::mtState>,
ImgOutlierDetection<typename FILTERSTATE::mtState>,false>{
    
void preProcess(mtFilterState& filterState, const mtMeas& meas, bool& isFinished){


}


void evalInnovation(mtInnovation& y, const mtState& state, const mtNoise& noise) const{
    
    Eigen::Vector2d pixError;
    pixError(0) = static_cast<double>(state.aux().feaCoorMeas_[ID].get_c().x - featureOutput_.c().get_c().x);
    pixError(1) = static_cast<double>(state.aux().feaCoorMeas_[ID].get_c().y - featureOutput_.c().get_c().y);
    y.template get<mtInnovation::_pix>() = pixError + noise.template get<mtNoise::_pix>();
}


}

world座標和imu座標的關係

template<unsigned int nMax, int nLevels, int patchSize,int nCam,int nPose>
class FilterState: public LWF::FilterState<State<nMax,nLevels,patchSize,nCam,nPose>,
            PredictionMeas,PredictionNoise<State<nMax,nLevels,patchSize,nCam,nPose>>,0>{

    void initWithAccelerometer(const V3D& fMeasInit) {
        V3D unitZ(0, 0, 1);
        if (fMeasInit.norm() > 1e-6) {
            state_.qWM().setFromVectors(fMeasInit, unitZ);
        } else {
            state_.qWM().setIdentity();
    }
    
}

影象部分主要的程式碼是

MultilevelPatchAlignement.hpp

這裡就是一個高斯牛頓法優化，目標點的位置。

bool align2D(FeatureCoordinates& cOut, const ImagePyramid<nLevels>& pyr, const MultilevelPatch<nLevels,patch_size>& mp,
        const FeatureCoordinates& cInit ,const int l1, const int l2, const int maxIter = 10, const double minPixUpd = 0.03){
    for(int iter = 0; iter<maxIter; ++iter){
        if(std::isnan(cOut.get_c().x) || std::isnan(cOut.get_c().y)){
            assert(false);
            return false;
        }
        if(!getLinearAlignEquations(pyr,mp,cOut,l1,l2,A_,b_)){
            return false;
        }
        svd_.compute(A_, Eigen::ComputeThinU | Eigen::ComputeThinV);
        if(svd_.nonzeroSingularValues()<2){
            return false;
        }
        update = svd_.solve(b_);
        cOut.set_c(cv::Point2f(cOut.get_c().x + update[0],cOut.get_c().y + update[1]),false);
        s = update[0]*update[0]+update[1]*update[1];
        if(s < min_update_squared){
            converged=true;
            break;
        }
    }
}

//這個函式就是上面那個怎麼構造影象塊畫素差作為EKF的更新
bool getLinearAlignEquations(const ImagePyramid<nLevels>& pyr, const MultilevelPatch<nLevels,patch_size>& mp,
                  const FeatureCoordinates& c, const int l1, const int l2,
                  Eigen::MatrixXf& A, Eigen::MatrixXf& b){

}

總結

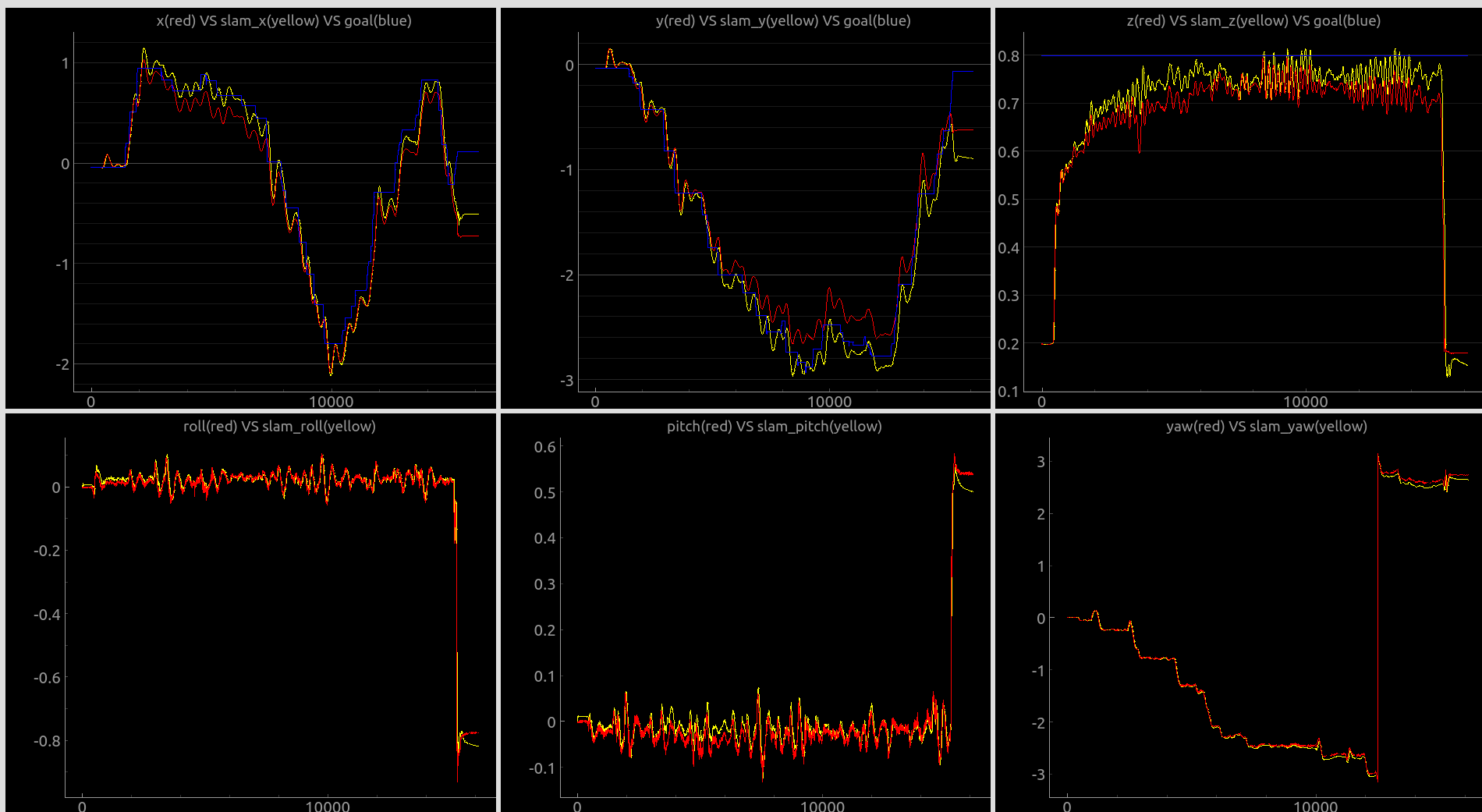
上面是我自己的無人機跑的和真實的運動捕捉系統的對比，是比較好的資料。說明在調的比較好的資料下是可以得到不錯的效果。(紅色是vrpn，黃色是rovio，藍色是我給飛機的設定點，紅色和黃色的差距還行，有時候比較大)

我使用的是EKF的優化是特徵點位置，要是換成IEKF，優化影象塊的畫素差，可能效果會更好。畢竟這東西是個高度非線性函式。

那個bearing vector的公式我還不會推導，對新增的feature　的initial depth的比較精確的估計對演算法精度有幫助，可以維護個地圖，

當然在地圖中做個local mapping thread，　也是可以的，但是感覺不能很好的和原來的演算法耦合起來就沒做。

這裡最需要改進的應該是特徵點的選取，原來演算法的效率太低了。而且會發現選取的很多特徵點不是那麼明顯的角點，有更好的選擇，不過為了保持距離的限制，妥協了。還有就是速度太慢了。

出現發散的情況，一般就是outlier太多了，沒有追蹤足夠的特徵點。因為速度發散，會導致影象更新為了矯正在特徵點深度位置上存在巨大的錯誤速度，把深度設到
無窮遠去，這樣影象更新就沒有作用，進一步導致速度發散。一發散就不可能回來了。