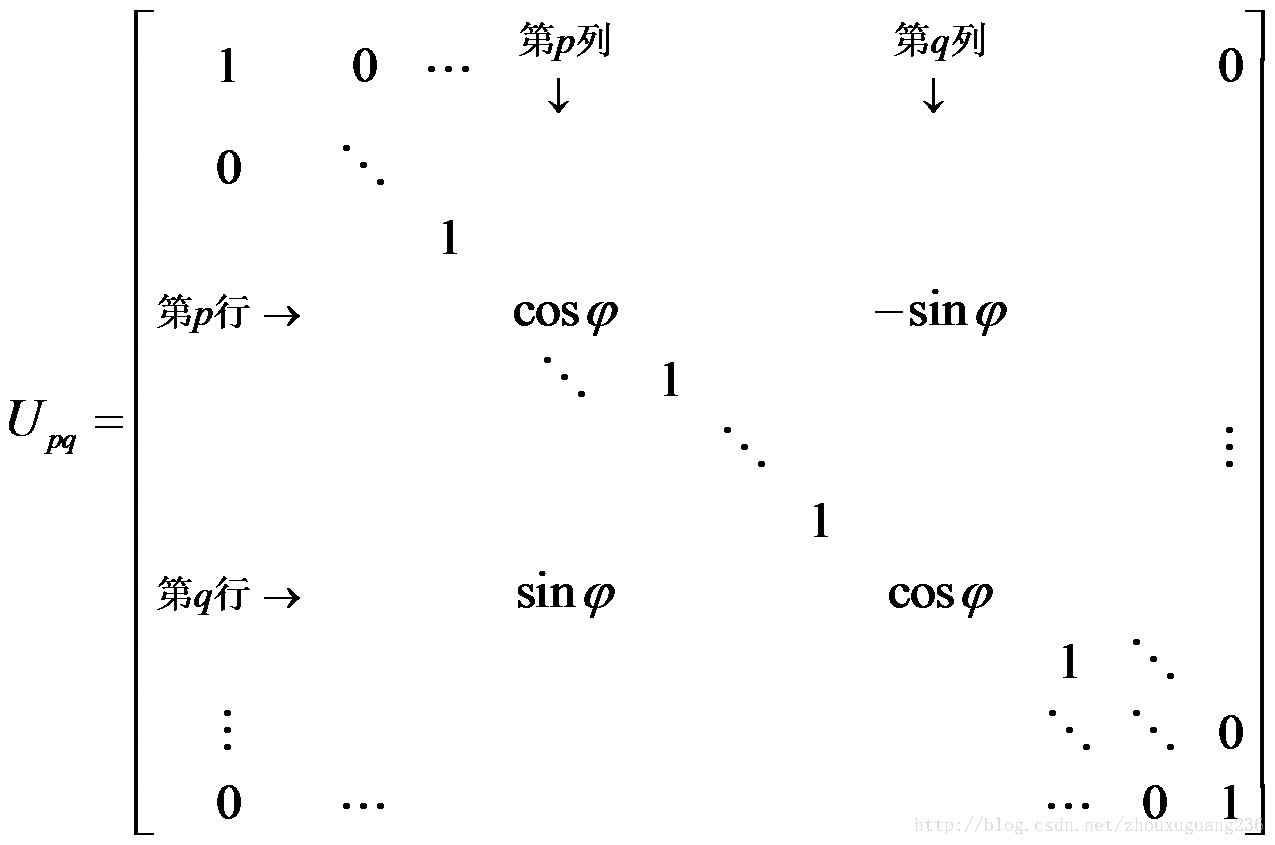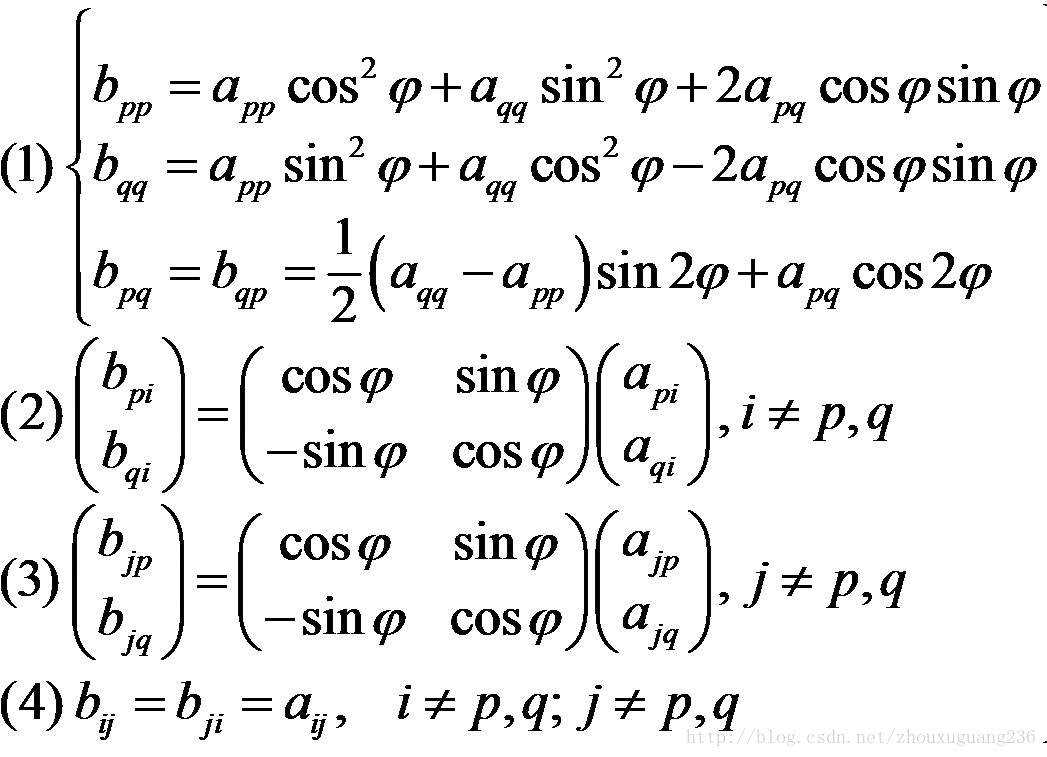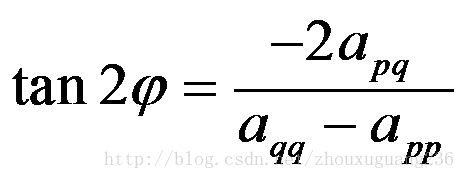矩陣的特徵值和特徵向量是線性代數以及矩陣論中非常重要的一個概念。在遙感領域也是經常用到，比如多光譜以及高光譜影象的主成分分析要求解波段間協方差矩陣或者相關係數矩陣的特徵值和特徵向量。

根據普通線性代數中的概念，特徵值和特徵向量可以用傳統的方法求得，但是實際專案中一般都是用數值分析的方法來計算，這裡介紹一下雅可比迭代法求解特徵值和特徵向量。

雅克比方法用於求實對稱陣的全部特徵值、特徵向量。

對於實對稱陣 A，必有正交陣 U，使

U ^TA U = D。

其中 D 是對角陣，其主對角線元 l_i 是 A 的特徵值. 正交陣 U 的第 j 列是 A 的屬於 l_i 的特徵向量。

原理：Jacobi 方法用平面旋轉對矩陣 A

既然用到了旋轉，這裡就介紹一下旋轉矩陣。

對於 p ≠ q,下面定義的 n 階矩陣U_pq 是平面旋轉矩陣。

容易驗證 U_pq是正交陣。對於向量x，U_pq x 相當於把座標軸Ox_p和 Ox_q 於所在的平面內旋轉角度 j .

變換過程: 在保證相似條件下，使主對角線外元素趨於零！

記 n 階方陣A = [a_ij],  對 A 做下面的變換：

A₁= U_pq^TAU_pq,                         

          A₁ 仍然是實對稱陣，因為，U_pq^T =U_pq^-1，知A₁與 A 的特徵值相同。

前面說了雅可比是一種迭代演算法，所以每一步迭代時，需要求出旋轉後新的矩陣，那麼新的矩陣元素如何求，這裡給出具體公式如下：

由上面的一組公式可以看到:

(1)矩陣A₁ 的第p 行、列與第 q 行、列中的元素髮生了變化，其它行、列中的元素不變。

(2)p、q分別是前一次的迭代矩陣A的非主對角線上絕對值最大元素的行列號

(3) j是旋轉角度，可以由下面的公式計算：

歸納可以得到雅可比迭代法求解矩陣特徵值和特徵向量的具體步驟如下：

(1) 初始化特徵向量為對角陣V，即主對角線的元素都是1.其他元素為0。

(2) 在A的非主對角線元素中，找到絕對值最大元素 a_{pq 。}

(3) 用式(3.14)計算tan2j，求 cosj, sinj 及矩陣U_{pq .}

(4) 用公式(1)-(4)求A₁；用當前特徵向量矩陣V乘以矩陣U_pq得到當前的特徵向量V。

(5) 若當前迭代前的矩陣A的非主對角線元素中最大值小於給定的閾值e時，停止計算；否則, 令A = A₁ , 重複執行(2) ~ (5)。 停止計算時，得到特徵值 l_i≈(A₁) _ij ，i,j= 1,2,…,n.以及特徵向量V。

(6) 這一步可選。根據特徵值的大小從大到小的順序重新排列矩陣的特徵值和特徵向量。

到現在為止，每一步的計算過程都十分清楚了，寫出程式碼也就不是難事了，具體程式碼如下：

/**
* @brief 求實對稱矩陣的特徵值及特徵向量的雅克比法 
* 利用雅格比(Jacobi)方法求實對稱矩陣的全部特徵值及特徵向量 
* @param pMatrix				長度為n*n的陣列，存放實對稱矩陣
* @param nDim					矩陣的階數 
* @param pdblVects				長度為n*n的陣列，返回特徵向量(按列儲存) 
* @param dbEps					精度要求 
* @param nJt					整型變數，控制最大迭代次數 
* @param pdbEigenValues			特徵值陣列
* @return 
*/
bool CPCAAlg::JacbiCor(double * pMatrix,int nDim, double *pdblVects, double *pdbEigenValues, double dbEps,int nJt)
{
	for(int i = 0; i < nDim; i ++) 
	{   
		pdblVects[i*nDim+i] = 1.0f; 
		for(int j = 0; j < nDim; j ++) 
		{ 
			if(i != j)   
				pdblVects[i*nDim+j]=0.0f; 
		} 
	} 

	int nCount = 0;		//迭代次數
	while(1)
	{
		//在pMatrix的非對角線上找到最大元素
		double dbMax = pMatrix[1];
		int nRow = 0;
		int nCol = 1;
		for (int i = 0; i < nDim; i ++)			//行
		{
			for (int j = 0; j < nDim; j ++)		//列
			{
				double d = fabs(pMatrix[i*nDim+j]); 

				if((i!=j) && (d> dbMax)) 
				{ 
					dbMax = d;   
					nRow = i;   
					nCol = j; 
				} 
			}
		}

		if(dbMax < dbEps)     //精度符合要求 
			break;  

		if(nCount > nJt)       //迭代次數超過限制
			break;

		nCount++;

		double dbApp = pMatrix[nRow*nDim+nRow];
		double dbApq = pMatrix[nRow*nDim+nCol];
		double dbAqq = pMatrix[nCol*nDim+nCol];

		//計算旋轉角度
		double dbAngle = 0.5*atan2(-2*dbApq,dbAqq-dbApp);
		double dbSinTheta = sin(dbAngle);
		double dbCosTheta = cos(dbAngle);
		double dbSin2Theta = sin(2*dbAngle);
		double dbCos2Theta = cos(2*dbAngle);

		pMatrix[nRow*nDim+nRow] = dbApp*dbCosTheta*dbCosTheta + 
			dbAqq*dbSinTheta*dbSinTheta + 2*dbApq*dbCosTheta*dbSinTheta;
		pMatrix[nCol*nDim+nCol] = dbApp*dbSinTheta*dbSinTheta + 
			dbAqq*dbCosTheta*dbCosTheta - 2*dbApq*dbCosTheta*dbSinTheta;
		pMatrix[nRow*nDim+nCol] = 0.5*(dbAqq-dbApp)*dbSin2Theta + dbApq*dbCos2Theta;
		pMatrix[nCol*nDim+nRow] = pMatrix[nRow*nDim+nCol];

		for(int i = 0; i < nDim; i ++) 
		{ 
			if((i!=nCol) && (i!=nRow)) 
			{ 
				int u = i*nDim + nRow;	//p  
				int w = i*nDim + nCol;	//q
				dbMax = pMatrix[u]; 
				pMatrix[u]= pMatrix[w]*dbSinTheta + dbMax*dbCosTheta; 
				pMatrix[w]= pMatrix[w]*dbCosTheta - dbMax*dbSinTheta; 
			} 
		} 

		for (int j = 0; j < nDim; j ++)
		{
			if((j!=nCol) && (j!=nRow)) 
			{ 
				int u = nRow*nDim + j;	//p
				int w = nCol*nDim + j;	//q
				dbMax = pMatrix[u]; 
				pMatrix[u]= pMatrix[w]*dbSinTheta + dbMax*dbCosTheta; 
				pMatrix[w]= pMatrix[w]*dbCosTheta - dbMax*dbSinTheta; 
			} 
		}

		//計算特徵向量
		for(int i = 0; i < nDim; i ++) 
		{ 
			int u = i*nDim + nRow;		//p   
			int w = i*nDim + nCol;		//q
			dbMax = pdblVects[u]; 
			pdblVects[u] = pdblVects[w]*dbSinTheta + dbMax*dbCosTheta; 
			pdblVects[w] = pdblVects[w]*dbCosTheta - dbMax*dbSinTheta; 
		} 

	}

	//對特徵值進行排序以及重新排列特徵向量,特徵值即pMatrix主對角線上的元素
	std::map<double,int> mapEigen;
	for(int i = 0; i < nDim; i ++) 
	{   
		pdbEigenValues[i] = pMatrix[i*nDim+i];

		mapEigen.insert(make_pair( pdbEigenValues[i],i ) );
	} 

	double *pdbTmpVec = new double[nDim*nDim];
	std::map<double,int>::reverse_iterator iter = mapEigen.rbegin();
	for (int j = 0; iter != mapEigen.rend(),j < nDim; ++iter,++j)
	{
		for (int i = 0; i < nDim; i ++)
		{
			pdbTmpVec[i*nDim+j] = pdblVects[i*nDim + iter->second];
		}

		//特徵值重新排列
		pdbEigenValues[j] = iter->first;
	}

	//設定正負號
	for(int i = 0; i < nDim; i ++) 
	{
		double dSumVec = 0;
		for(int j = 0; j < nDim; j ++)
			dSumVec += pdbTmpVec[j * nDim + i];
		if(dSumVec<0)
		{
			for(int j = 0;j < nDim; j ++)
				pdbTmpVec[j * nDim + i] *= -1;
		}
	}

	memcpy(pdblVects,pdbTmpVec,sizeof(double)*nDim*nDim);
	delete []pdbTmpVec;

	return 1;
}