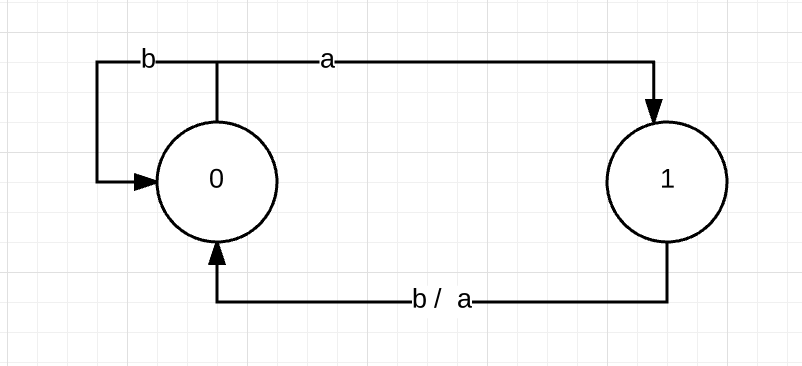
字串匹配自動機的演算法原理
上一節,我們知道,如何構造一個有限狀態機,用於字串匹配,我們只給出了怎麼做,這一節,我們詳細說明一下,為什麼要這麼做,我們要從數學上驗證上一節我們給出的演算法邏輯是經得起考驗的。
如上圖所示,有限狀態自動機有以下幾個特點:
1. 它由一系列的狀態節點組成,我們用Q來表示這些節點的集合
2. 狀態機一開始就會處於初始狀態,我們用
3. 所以狀態中,必有一個狀態A
4. 組成字串的字符集
5. 當狀態機處於某個狀態,接收到一個輸入字元時,會跳轉到另一個狀態,這種跳轉我們用一個函式
我們再引入一個函式
狀態機一開始時,處於初始狀態,也就是狀態機什麼都不接收時或接收空字串時就處於初始狀態,於是我們有:
假設w 是一個字串,那麼有:
上面這個公式需要好好解釋一下,假定w=”aabb”, wa = “aabb” + ‘a’ = “aabba”.
當狀態機接收字串”aabb”後,處於狀態0,於是就有
數學推理是一個比較燒腦的過程,想必上面的解釋會讓不少同學抓耳撓腮一陣子。
假設要查詢的字串,我們用P來表示,對於給定一個文字T, 如果P 的前k個字元所組成的字串是T的字尾的話,我們就定義:
例如 P=”abcdefg”, T = “hhhhhhhha”, 那麼P的前1個字元所組成的字串”a”是T的字尾,所以
T=”hhhhhhab”, 那麼P的前兩個字元組成的字串”ab”構成T的字尾,於是
T=”hhhhhabc”, P的前3個字元組成的字串”abc”構成T的字尾,於是有
依次類推。
上一節我們構造的狀態機是滿足以下條件的:
1. 如果P 含有m個字元,那麼狀態機就有m+1個狀態節點,他們分別為{0,1,2…m}, 並且初始狀態
2. 當狀態機處於狀態q時,如果接收字元a, 那麼狀態機要跳轉的下一個狀態是:
上一節我們給出的程式碼有這麼一段:
private void makeJumpTable() {
int m = P.length();
for (int q = 0; q <= m; q++) {
for (int k = 0; k < alphaSize; k++) {
char c = (char)('a' + k);
String Pq = P.substring(0, q) + c;
int nextState = findSuffix(Pq);
System.out.println("from state " + q + " receive input char " + c + " jump to state " + nextState);
HashMap<Character, Integer> map = jumpTable.get(q);
if (map == null) {
map = new HashMap<Character, Integer>();
}
map.put(c, nextState);
jumpTable.put(q, map);
}
}String Pq = P.substring(0, q) + c; 這一句程式碼的作用,其實就是構造字串
如果我們能夠證明,我們前一節構造的狀態機滿足:
定理1:
對給定的匹配字串P, 以及文字x, 還有任意字元a, 我們有:
令r =
由於
定理2:
對匹配字串P, 文字字串x, 以及任意一個字元a, 如果 q =
先看個具體例項,P=”bacdb”, x=”ffffb”, 1 = q =
xa = “ffffba”, 於是2 = q =