什麼叫有限狀態自動機

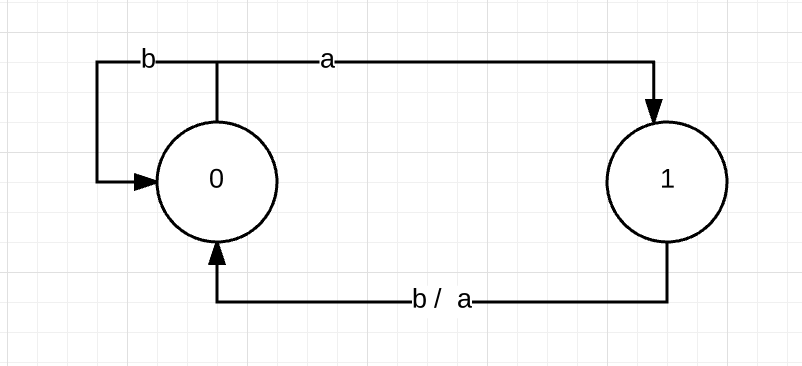
先看一個圖：

上面這個圖描述的就叫一個有限狀態自動機，圖中兩個圓圈，也叫節點，用於表示狀態，從圖中可以看成，它有兩個狀態，分別叫0和1. 從每個節點出發，都會有若干條邊，當處於某個狀態時，如果輸入的字元跟該節點出發的某條邊的內容一樣，那麼就會引起狀態的轉換。例如，如果當前狀態處於0，輸入是字元a,那麼狀態機就會從狀態0進入狀態1.如果當前狀態是1，輸入字元是b或a,那麼，狀態機就會從狀態1進入狀態0.如果當前所處的狀態，沒有出去的邊可以應對輸入的字元，那麼狀態機便會進入到錯誤狀態。例如，如果當前處於狀態0，輸入字元是c,那麼狀態機就會出錯，因為從狀態0開始，沒有哪條邊對應的字元是c.

狀態機會有一個初始節點，和一個接收節點，以上圖為例，我們可以設定初始節點為0，接收節點為1，當進行一系列的輸入，使得狀態機的狀態不斷變化，只要最後一個輸入使得狀態機處於接收節點，那麼就表明當前輸入可以被狀態機接收。例如對應字串”abaaa”, 從初始節點0開始，狀態機根據該字串的輸入所形成的狀態變化序列為：{0，1，0，1，0，1}。由於最後狀態機處於狀態1，所以該字串可以被狀態機接收。如果輸入的字串是:abbaa, 那麼狀態機的變化序列為：{0，1，0，0，1，0}， 由於最後狀態機處於非接收狀態，因此這個字串被狀態機拒絕。

在程式中，我們一般使用二維表來表示一個狀態機，例如上面的狀態機用二維表來表示如下：

通過查表，我們便可知道狀態機的轉換，例如處於狀態0，輸入字元是a時，我們從表中得到的數值是1，也就是說處於狀態0，輸入是字元a,那麼狀態機將轉入狀態節點1.

一個文字匹配流程的描述

接下來我們看看一個文字的匹配流程，假定要查詢的字串為P=”ababaca”, 被查詢的文字為T=”abababacaba”. 一次讀入T的一個字元，用S表示當前讀入的T的字元，一開始讀入一個字元，於是S=a.然後看看，從P開始，連續幾個字元所構成的字串可以成為S的字尾，由於當前S只有一個字元a,於是從P開始，連續1個字元所形成的字串”a”,可以作為S的字尾。把這個字串的長度記為k,於是此時k 等於1. 繼續從T中讀入字元，於是S=”ab”, 此時，從P開始，連續兩個字元所構成的字串”ab”可以作為S的字尾，於是k = 2.反覆這麼操作，於是便有以下序列：

1. S=a, k = 1, P[1] 是S的字尾
2. S=ab, k = 2, P[1,2] 是S的字尾
3. S=aba, k = 3, P[1,2,3]是S的字尾
4. S=abab, k= 4, P[1,2,3,4]是S的字尾
5. S=ababa, k = 5, P[1,2,3,4,5]是S的字尾
6. S=ababab, k = 4, P[1,2,3,4]是S的字尾
7. S=abababa, k = 5, P[1,2,3,4,5]是S的字尾
8. S=abababac, k = 6, P[1,2,3,4,5,6]是S的字尾
9. S=abababaca, k = 7, P[1,2,3,4,5,6,7]是S的字尾
10. S=abababacab, k =2, P[1,2] 是S的字尾
11. S=abababacaba, k = 3, P[1,2,3] 是S的字尾。

注意看第9步，P的長度是7，整個字串P成為了字串S的字尾，而此時的S是文字T的字首，這不就表明文字T含有字串P了嗎。在每一個步驟中，我們都需要從P的第一個字元開始，看看最多能連續讀取幾個字元，使得他們能成為S的字尾，假設P的字元個數為m, 那麼這個讀取過程最多需要讀取m個字元，於是複雜度為O(m). 如果有某種辦法，使得我們一次就可以知道從P開始，連續讀取幾個字元就可以構成S 的字尾，假設文字T含有n個字元，那麼我們就可以在O(n)的時間內判斷，T是否含有字串P.因為上面的步驟最多可以執行n次。

於是當前問題變成，構造一個方法，使得一次執行便能知道從P開始，連續讀取幾個字元能使，得這幾個字元構成的字串是S的字尾。這個方法，就需要上面我們提到的有限狀態自動機。

用於字串匹配的自動機

假定字串P和文字T只由a,b兩個字元組成，也就是字符集為∑={a,b,c}, P含有m個字母，於是，我們要構造的自動機就含有m個狀態節點。假設我們當前處於狀態節點q, 那麼當下一個輸入字元是a和b時，從當前節點q該跳轉到哪一個節點呢？ 如果用Pq來表示長度為q的P的字首，以q=4, p=”ababaca”, Pq=”abab”, 那麼當處於狀態4, 當輸入為a時，我們構造字串 S = Pq + ‘a’ = “ababa”, 然後看看字串P從第一個字元開始，連續幾個字元所構成的字串可以成為S的字尾，就當前S為例，從第一個字元開始，連續5個字元，也就是P[1,2,3,4,5]可以作為S的字尾，於是，我們就有，當狀態機處於節點4，輸入為a時，跳轉的下個狀態就是5. 同理，當處於狀態q=4,輸入為字元b時，S = Pq + ‘b’ = “ababb”,此時從P開始，連續讀取0個字元才能形成S的字尾，於是當狀態機處於狀態4，如果讀入字元是b, 那麼跳轉的下一個狀態是0，同理，如果輸入字元是c, 那麼S = Pq + ‘c’ = “ababc”, 此時從P開始，連續讀取0個字元所形成的空字串才能作為S的字尾，於是當狀態機處於狀態節點4，輸入字元為c時，跳轉到節點0. 如果q從0開始，一直到m,反覆運用剛才提到的步驟，便會產生下面這個跳轉表：

利用上面的狀態機，依次讀入T的字元，如果狀態機跳轉到狀態q,那就表明從P的第一個字元開始，連續讀取q個字元，所形成的字串可以構成是S的字尾，也就是說，當我們的狀態機跳轉到狀態7時，我們就可以得知文字T,包含字串P.

我們走一遍這個過程，首先狀態機處於狀態0，讀入T[0]=a, S= a, 查表可知進入狀態1，讀入T[1]=b, S=ab, 查表可知，進入狀態2，讀入T[2]=a,查表可知進入狀態3，讀入T[3]=b, S=abab,查表可知進入狀態4，讀入T[4]=a,S=ababa,查表可知進入狀態5，讀入T[5]=b,S=ababab,查表可知進入狀態4，讀入T[6]=a, S=abababa,查表可知進入狀態5，讀入T[7]=c,S=abababac,查表可知進入狀態6，讀入T[8]=a,S=abababaca,查表可知進入狀態7，此時，我們可以得出結論，文字T包含有字串P.

程式碼實現

import java.util.HashMap;


public class StringAutomaton {
   private HashMap<Integer, HashMap<Character, Integer>> jumpTable = new HashMap<Integer, HashMap<Character, Integer>>();
   String P = "";
   private final int alphaSize = 3;
   public StringAutomaton(String p) {
       this.P = p;
       makeJumpTable();
   }

   private void makeJumpTable() {
       int m = P.length();
       for (int q = 0; q <= m; q++) {
           for (int k = 0; k < alphaSize; k++) {

               char c = (char)('a' + k);
               String Pq = P.substring(0, q) + c;


               int nextState = findSuffix(Pq);
               System.out.println("from state " + q + " receive input char " + c + " jump to state " + nextState);
               HashMap<Character, Integer> map = jumpTable.get(q);
               if (map == null) {
                   map = new HashMap<Character, Integer>();
               }

               map.put(c, nextState);
               jumpTable.put(q, map);
           }
       }
   }

   private int findSuffix(String Pq) {
       int suffixLen = 0;
       int k = 0;

       while(k < Pq.length() && k < P.length()) {
           int i = 0;
           for (i = 0; i <= k; i++) {
               if (Pq.charAt(Pq.length() - 1 - k + i) != P.charAt(i)) {
                   break;
               }
           }

           if (i - 1 == k) {
              suffixLen = k+1;
           } 

           k++;
       }

       return suffixLen;
   }

   public int match(String T) {
       Integer q = 0;
       System.out.println("Begin matching...");

       for (int n = 0; n <= T.length(); n++) {
           HashMap<Character, Integer> map = jumpTable.get(q);
           int oldState = q;
           q = map.get(T.charAt(n));
           if (q == null) {
               return -1;
           }

           System.out.println("In state " + oldState + " receive input " + T.charAt(n) + " jump to state " + q);

           if (q == P.length()) {
               return q;
           }
       }

       return -1;
   }
}

程式碼中，makeJumpTable呼叫用來構建跳轉表，findSuffix用來查詢最大的數值K, 使得P[1…k] 是字串Pq的字尾，該呼叫有兩層迴圈，所以複雜度是O(m2), makeJumpTable有兩層迴圈，迴圈次數為O(m*|∑|), 所以makeJumpTable總的時間複雜度為O(m3|∑|), 也就是說，構建跳轉表的複雜度是：O(m3|∑|)。

match依靠跳轉表來判斷，輸入的字串T是否包含字串P,如果T的最後一個字元輸入狀態機後，從跳轉表得到的狀態的值等於P的長度m,那麼表明T包含字串P.具體的程式除錯過程請參看視訊。

我們只給出了演算法的實現流程，演算法的數學原理比較複雜，我們將在下一節詳解。