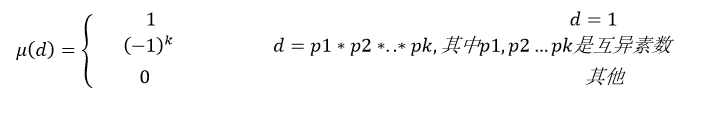bzoj 2440 -莫比烏斯函式的應用 + 容斥原理
連結:http://www.lydsy.com/JudgeOnline/problem.php?id=2440
Description
小 X 自幼就很喜歡數。但奇怪的是,他十分討厭完全平方數。他覺得這些
數看起來很令人難受。由此,他也討厭所有是完全平方數的正整數倍的數。然而
這絲毫不影響他對其他數的熱愛。
這天是小X的生日,小 W 想送一個數給他作為生日禮物。當然他不能送一
個小X討厭的數。他列出了所有小X不討厭的數,然後選取了第 K個數送給了
小X。小X很開心地收下了。
然而現在小 W 卻記不起送給小X的是哪個數了。你能幫他一下嗎?
Input
包含多組測試資料。檔案第一行有一個整數 T,表示測試
資料的組數。
第2 至第T+1 行每行有一個整數Ki,描述一組資料,含義如題目中所描述。
Output
含T 行,分別對每組資料作出回答。第 i 行輸出相應的
第Ki 個不是完全平方數的正整數倍的數。
Sample Input
41
13
100
1234567
Sample Output
119
163
2030745
HINT
對於 100%的資料有 1 ≤ Ki ≤ 10^9
, T ≤ 50
關於莫比烏斯函式mu,他的定義如下:
因此 我們對 i=1:sqrt(x) 累加一遍,係數為mu(i),便可得到答案。
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll p =1000000007;
const int N=100000;
bool is_prime[N+500];
int prime[N+50];
int mu[N+50];
ll tot;
void Moblus()
{
tot = 0;
mu[1] = 1;
for(ll i = 2; i < N; i++)
{
if(!is_prime[i])
{
prime[tot++] = i;
mu[i] = -1;
}
for(ll j = 0; j < tot && i*prime[j] < N; j++)
{
is_prime[i*prime[j]] = 1;
if(i % prime[j])
{
mu[i*prime[j]] = -mu[i];
}
else
{
mu[i*prime[j]] = 0;
break;
}
}
}
}
ll ok(ll x)
{
ll ret=0;
for (ll i=1;i*i<=x;i++)
ret+= x/(i*i)*mu[i];
return ret;
}
int main()
{
Moblus();
int t;cin>>t;
while(t--)
{
ll k;
scanf("%lld",&k);
ll l=1,r=1e10,ans=-1;
while(l<=r)
{
ll mid=(l+r)>>1;
if (ok(mid)>=k)
r=mid-1,ans=mid;
else l=mid+1;
}
printf("%lld\n",ans);
}
return 0;
}
相關推薦
bzoj 2440 -莫比烏斯函式的應用 + 容斥原理
連結:http://www.lydsy.com/JudgeOnline/problem.php?id=2440 Description 小 X 自幼就很喜歡數。但奇怪的是,他十分討厭完全平方數。他
hdu 6053 莫比烏斯函式(容斥)
題意:兩個序列,A,B,A序列給出,Bi<=Ai,問滿足所有區間的gcd l r != 1 的B序列的方案數 思路:列舉B整體的GCD,直接列舉顯然會重複計算,顧使用莫比烏斯進行容斥,單組因子的方案數就是sum (ai/p) 顯然直接列舉時間複雜度為n*m m=m
bzoj2301 [HAOI2011]Problem b(求gcd==k的個數)(莫比烏斯反演+容斥原理)
首先我們搞掉下界,怎麼搞呢,用容斥原理即可。(看做矩形區間),然後我們需要求∑x=1n∑y=1ngcd(x,y)==k。 ∑x=1⌊n/k⌋∑y=1⌊m/k⌋gcd(x,y)==1 ∑x=1⌊n/k
5072 單色三角形+莫比烏斯反演+容斥原理
單色三角形:如果每個人都有關係的話,認識或者不認識,隨便找6個人(或以上),則一定會有三個人互相認識,或者互相不認識。因為每個人和其他人都有關係嘛,認識或者不認識。則一個人A與其他5個人有都有關係,這個時候當A與其他5個人的關係中有兩個認識,3個不認識(或者2個
HDU 6053 TrickGCD 莫比烏斯函數/容斥/篩法
mem define brush double 容斥 sum main cas sca 題意:給出n個數$a[i]$,每個數可以變成不大於它的數,現問所有數的gcd大於1的方案數。其中$(n,a[i]<=1e5)$ 思路:鑒於a[i]不大,可以想到枚舉gcd的值。考
6053 TrickGCD(莫比烏斯反演+容斥思想+分塊字首和技巧)
題目大意: 給你一個數組 A ,問你有多少不大於 A 的陣列 B 使得 B 中所有元素的最大公因數不為1。(陣列 B 不大於陣列 A 就等價於,對於任意 A 陣列中的元素 a [ i ] 和 B 陣列中對應元素 b [ i ] ,均有:a [ i ] >
TrickGCD(莫比烏斯反演+容斥定理)
連結:http://acm.hdu.edu.cn/showproblem.php?pid=6053 hdu6053 TrickGCD 題目解析: 令sum[k]為k能夠出現的個數 eg: Input 3 6 6 9 各個數字出現的情況 1 1 1 2 2 2 3 3
F - Tmutarakan Exams URAL - 1091 -莫比烏斯函數-容斥 or DP計數
strong get rime oid ofo lld 們的 else max F - Tmutarakan Exams 題意 : 從 < = S 的 數 中 選 出 K 個 不 同 的 數 並 且 gcd > 1 。求方案數。 思路 :記 錄 一 下 每 個
C - Visible Trees HDU - 2841 -莫比烏斯函數-容斥
main efi light esp amp prime scanf break sca C - Visible Trees HDU - 2841 思路 :被擋住的那些點(x , y)肯定是 x 與 y不互質。能夠由其他坐標的倍數表示,所以就轉化成了求那些點 x,
[BZOJ2301]Problem b 莫比烏斯反演+容斥
題意明確,就是求∑i=ab∑j=cdgcd(i,j)==k 首先容易發現容斥定理,轉化為求 ∑i=1n∑j=1mgcd(i,j)==k 我們設f(d)=∑i=1n∑j=1m(gcd(i,j)==d
BZOJ 2440 淺談莫比烏斯函式性質推導
世界真的很大 莫比烏斯絕不是隻有反演而已,其本身就是一個非常值得專研的函式 本質上來講大概是指容斥時的係數規劃,但也由此演化出了各種各樣的有意思的東西 看題先: description
bzoj 2440 完全平方數 【莫比烏斯函式】
題目 題意:第Ki 個不是完全平方數的正整數倍的數。 對於一個數t,t以內的數裡的非完全平方數倍數的個數:num=1的倍數的數量−一個質數平方數(9,25,49...)的倍數的數量+兩個質數的積平方數(36,100,225...)的數量−三個質數balabala…… 所
BZOJ 2440 完全平方數(莫比烏斯函式+容斥)
注意的兩點是二分的時候注意,要選取最小的那個答案,因為19是13個,20也是13個,而很明顯19才是符合答案的。 還有感覺題目給的資料範圍不對,實際比較大,所以二分的時候r大點。 #include<bits/stdc++.h> using nam
BZOJ 2440 完全平方數-莫比烏斯函式
題目描述 1.n的不大確定+f(n)([1,n]中不是平方數的倍數的數的個數)遞增 -> 二分 2.容斥原理:f(x)=1的倍數-一個質數的倍數+2個質數乘積的倍數-… ;
BZOJ 3930 選數(莫比烏斯函式+杜教篩)
#include<bits/stdc++.h> using namespace std; #define debug puts("YES"); #define rep(x,y,z) for(int (x)=(y);(x)<(z);(x)++) #def
BZOJ 2301 莫比烏斯反演入門
思想 phi 問題 ace tail main pro html 簡單的 2301: [HAOI2011]Problem b Description 對於給出的n個詢問,每次求有多少個數對(x,y),滿足a≤x≤b,c≤y≤d,且gcd(x,y) = k,gcd(x,
BZOJ - 2818 莫比烏斯反演 初步
queue oid tor break bzoj char class rime 技巧 要使用分塊的技巧 #include<iostream> #include<algorithm> #include<cstdio> #include&l
BZOJ - 2005 莫比烏斯水題
OS println register tdi span () reg bre pre \(gcd=k+1\)時,每一個的貢獻都是\(2k+1\) \(gcd=1\)時,每一個貢獻為\(1\) #include<iostream> #include<alg
計蒜客 青雲的機房組網方案(莫比烏斯函式+樹上dsu)
題意 給定一棵 n n n 個節點的樹,每個節點上有一個點權,邊權為均
【模板】莫比烏斯函式
#include<bits/stdc++.h> using namespace std; const int MAXN = 1000000; bool check[MAXN+10]; int prime[MAXN+10]; int mu[MAXN+10]; void Mobius() {