【模式匹配】KMP演算法的來龍去脈
1. 引言
字串匹配是極為常見的一種模式匹配。簡單地說,就是判斷主串\(T\)中是否出現該模式串\(P\),即\(P\)為\(T\)的子串。特別地,定義主串為\(T[0 \dots n-1]\),模式串為\(P[0 \dots p-1]\),則主串與模式串的長度各為\(n\)與\(p\)。
暴力匹配
暴力匹配方法的思想非常樸素:
- 依次從主串的首字元開始,與模式串逐一進行匹配;
- 遇到失配時,則移到主串的第二個字元,將其與模式串首字元比較,逐一進行匹配;
- 重複上述步驟,直至能匹配上,或剩下主串的長度不足以進行匹配。
下圖給出了暴力匹配的例子,主串T="ababcabcacbab",模式串P="abcac"
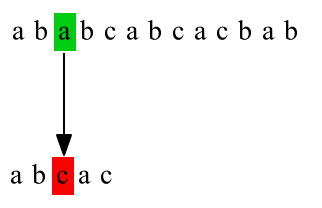
第二次匹配:

第三次匹配:
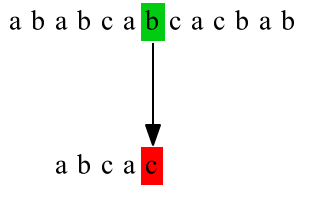
C程式碼實現:
int brute_force_match(char *t, char *p) { int i, j, tem; int tlen = strlen(t), plen = strlen(p); for(i = 0, j = 0; i <= tlen - plen; i++, j = 0) { tem = i; while(t[tem] == p[j] & j < plen) { tem++; j++; } // matched if(j == plen) { return i; } } // [p] is not a substring of [t] return -1; }
時間複雜度:i在主串移動次數(外層的for迴圈)有\(n-p\)次,在失配時j移動次數最多有\(p-1\)次(最壞情況下);因此,複雜度為\(O(n*p)\)。
我們仔細觀察暴力匹配方法,發現:失配後下一次匹配,
- 主串的起始位置 = 上一輪匹配的起始位置 + 1;
- 模式串的起始位置 = 首字元
P[0]。
如此未能利用已經匹配上的字元的資訊,造成了重複匹配。舉個例子,比如:第一次匹配失敗時,主串、模式串失配位置的字元分別為 a 與 c,下一次匹配時主串、模式串的起始位置分別為T[1]與P[0];而在模式串中c之前是ab,未有重複字元結構,因此T[1]與P[0]肯定不能匹配上,這樣造成了重複匹配。直觀上,下一次的匹配應從T[2]
P[0]開始。
2. KMP演算法
KMP思想
根據暴力方法的缺點,而引出KMP演算法的思想。首先,一般化匹配失敗,如下圖所示:

在暴力匹配方法中,下一次匹配開始時,主串指標會回溯到i+1,模式串指標會回退到0。那麼,如果不讓主串指標發生回溯,模式串的指標應回退到哪個位置才能保證正確匹配呢?首先,我們從上圖中可以得到已匹配上的字元:
\[ T[i \dots i+j-1] = P[0 \dots j-1] \]
KMP演算法思想便是利用已經匹配上的字元資訊,使得模式串的指標回退的字元位置能將主串與模式串已經匹配上的字元結構重新對齊。當有重複字元結構時,下一次匹配如下圖所示:

從圖中可以看出,下一次匹配開始時,主串指標在失配位置i+j,模式串指標回退到m+1;模式串的重複字元結構:
\begin{equation}
T[i+j-m-1 \dots i+j-1] = P[j-m-1 \dots j-1] = P[0 \dots m]
\label{eq:overlap}
\end{equation}
且有
\[ T[i+j] \neq P[j] \neq P[m+1] \]
那麼應如何選取\(m\)值呢?假定有滿足式子\eqref{eq:overlap}的兩個值\(m_1 > m_2\),如下圖所示:
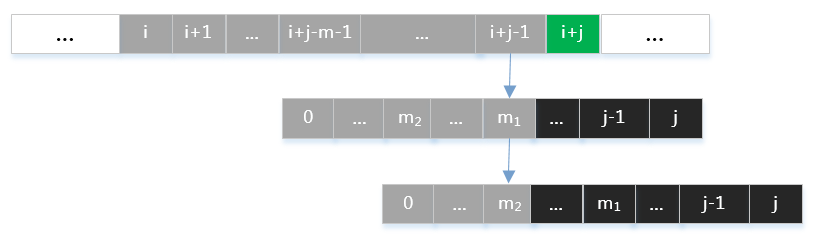
如果選取\(m=m_2\),則會丟失\(m=m_1\)的這一種字元匹配情況。由數學歸納法容易知道,應取所有滿足式子\eqref{eq:overlap}中最大的\(m\)值。
KMP演算法中每一次的匹配,
- 主串的起始位置 = 上一輪匹配的失配位置;
- 模式串的起始位置 = 重複字元結構的下一位字元(無重複字元結構,則模式串的首字元)
模式串P="abcac"匹配主串T="ababcabcacbab"的KMP過程如下圖:
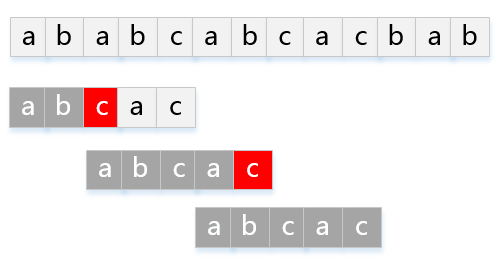
部分匹配函式
根據上面的討論,我們定義部分匹配函式(Partial Match,在資料結構書[2]稱之為失配函式):
\[ f(j) = \left\{ {\matrix{ {\max \{ m \} } & P[0\dots m]=P[{j-m}\dots {j}],0\le m < j \cr {-1} & else \cr } } \right. \]
其表示字串\(P[0 \dots j]\)的字首與字尾完全匹配的最大長度,也表示了模式串中重複字元結構資訊。KMP中大名鼎鼎的next[j]函式表示對於模式串失配位置j+1,下一輪匹配時模式串的起始位置(即對齊於主串的失配位置);則
\[ next[j] = f(j)+1 \]
如何計算部分匹配函式呢?首先來看一個例子,模式串P="ababababca"的部分匹配函式與next函式如下:
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| P[j] | a | b | a | b | a | b | a | b | c | a |
| f(j) | -1 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | -1 | 0 |
| next[j] | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 |
模式串的f(j)滿足\(P[0 \dots f(j)]=P[j-f(j) \dots j]\),在計算f(j+1)分為兩類情況:
- 若\(P[j+1]=P[f(j)+1]\),則有\(P[0 \dots f(j)+1]=P[j-f(j) \dots j+1]\),因此
f(j+1)=f(j)+1。 - 若\(P[j+1] \neq P[f(j)+1]\),則要從\(P[0 \dots f(j)]\)中找出滿足
P[f(j+1)]=P[j+1]的f(j+1),從而得到\(P[0 \dots f(j+1)]=P[j+1-f(j+1) \dots j+1]\)
其中,根據f(j)的定義有:
\[ P[j]=P[f(j)]=P[f(f(j))]=\cdots = P[f^k(j)] \]
其中,\(f^k(j)=f(f^{k-1}(j))\)。通過上面的例子可知,函式\(f^k(j)\)是隨著\(k\)遞減的,並最後收斂於-1。此外,P[j]與p[j+1]相鄰;因此若存在P[f(j+1)]=P[j+1],則必有
\[ f(j+1)=f^k(j)+1 \]
為了求滿足條件的最大的f(j+1),因\(f^k(j)\)是隨著\(k\)遞減的,故應為滿足上式的最小\(k\)值。
綜上,部分匹配函式的計算公式如下:
\[ f(j) = \left\{ {\matrix{ {f^k(j-1)+1} & \min \limits_{k} P[f^k(j-1)+1]=P[j] \cr {-1} & else \cr } } \right. \]
程式碼實現
部分匹配函式(失配函式)的C實現程式碼:
int *fail(char *p) {
int len = strlen(p);
int *f = (int *) malloc(len * sizeof(int));
f[0] = -1;
int i, j;
for(j = 1; j < len; j++) {
for(i = f[j-1]; ; i = f[i]) {
if(p[j] == p[i+1]) {
f[j] = i + 1;
break;
}
else if(i == -1) {
f[j] = -1;
break;
}
}
}
return f;
}KMP的C實現程式碼:
int kmp(char *t, char *p) {
int *f = fail(p);
int i, j;
for(i = 0, j = 0; i < strlen(t) && j < strlen(p); ) {
if(t[i] == p[j]) {
i++;
j++;
}
else if(j == 0)
i++;
else
j = f[j-1] + 1;
}
return j == strlen(p) ? i - strlen(p) : -1;
}時間複雜度:fail函式的複雜度為\(O(p)\),kmp函式的複雜度為\(O(n)\),所以整個KMP演算法的複雜度為\(O(n+p)\)。
3. 參考資料
相關推薦
【模式匹配】KMP演算法的來龍去脈
1. 引言 字串匹配是極為常見的一種模式匹配。簡單地說,就是判斷主串\(T\)中是否出現該模式串\(P\),即\(P\)為\(T\)的子串。特別地,定義主串為\(T[0 \dots n-1]\),模式串為\(P[0 \dots p-1]\),則主串與模式串的長度各為\(n\)與\(p\)。 暴力匹配 暴力匹配
【模式匹配】之 —— KMP演算法詳解及證明
本文所述KMP演算法原始碼可在這裡下載: Name Date Reason for change Revision 超然 2013.03.19 First version 1.0 超然 2013.04.15 Added
【模式匹配】更快的Boyer-Moore演算法
1. 引言 前一篇中介紹了字串KMP演算法,其利用失配時已匹配的字元資訊,以確定下一次匹配時模式串的起始位置。本文所要介紹的Boyer-Moore演算法是一種比KMP更快的字串匹配演算法,它到底是怎麼快的呢?且聽下面分解。 不同於KMP在匹配過程中從左至右與主串字元做比較,Boyer-Moore演算法是從模式
【面試題】KMP演算法實現
what!? KMP演算法是幹嘛的? 我們可能都知道樸素演算法,主要是解決兩個字串的匹配問題,其實KMP演算法可以說和樸素演算法是師出同門,為什麼這麼講呢?首先我們對比一下兩個的程式碼,大家就知道怎麼回事了。 樸素演算法 int BF(const char *str1
演算法:模式匹配之KMP演算法
前言: 昨天看到《演算法導論》裡的第32章:字串匹配,說到一個關於字串匹配的很好的演算法——KMP。關於KMP的記憶體含意以及KMP的來源,不是本文講述的範疇,請感興趣的讀者自行查閱相關資料。
【特徵匹配】RANSAC演算法原理與原始碼解析
轉載請註明出處:http://blog.csdn.net/luoshixian099/article/details/50217655 勿在浮沙築高臺 隨機抽樣一致性(RANSAC)演算法,可以在一組包含“外點”的資料集中,採用不斷迭代的方法,尋找最優引數模型,不符合最
【模式匹配】Aho-Corasick自動機
1. 多模匹配 AC自動機(Aho-Corasick Automaton)是多模匹配演算法的一種。所謂多模匹配,是指在字串匹配中,模式串有多個。前面所介紹的KMP、BM為單模匹配,即模式串只有一個。假設主串\(T[1 \cdots m]\),模式串有k個\(\mathbb{P} = \{ P_1, \cdot
【資料結構與演算法】模式匹配——從BF演算法到KMP演算法(附完整原始碼)
模式匹配子串的定位操作通常稱為串的模式匹配。模式匹配的應用很常見,比如在文書處理軟體中經常用到的查詢功能。我們用如下函式來表示對字串位置的定位:int index(const string &T
【算法】KMP字符串匹配算法
str 字符 amp mage closed oid () hid aps 【原理】 (1)next數組原理 (2)特殊情況的處理(巧妙增設哨兵) (3)遞推法構造next[]表 【實現代碼】 #include<iostream> #incl
【字串匹配】【BKDRhash||KMP】
題目描述 給定一個字串 A 和一個字串 B ,求 B 在 A 中的出現次數。A 和 B中的字元均為英語大寫字母或小寫字母。 A 中不同位置出現的 B 可重疊。 輸入格式 輸入共兩行,分別是字串 A 和字串 B 。 輸出格式 輸出一個整數,表示 B 在 A 中的出現次數。
模式串匹配之KMP演算法詳解
KMP演算法,是由Knuth,Morris,Pratt共同提出的模式匹配演算法,其對於任何模式和目標序列,都可以線上性時間內完成匹配查詢,而不會發生退化,是一個非常優秀的模式匹配演算法。但是相較於其他模式匹配演算法,該演算法晦澀難懂,第一次接觸該演算法的讀者往往會看得一頭
【模式識別】K-近鄰分類演算法KNN
K-近鄰(K-Nearest Neighbors, KNN)是一種很好理解的分類演算法,簡單說來就是從訓練樣本中找出K個與其最相近的樣本,然後看這K個樣本中哪個類別的樣本多,則待判定的值(或說抽樣)就屬於這個類別。KNN演算法的步驟計算已知類別資料集中每個點與當前點的距離;選
串的模式匹配(BF演算法,KMP演算法)
第一位的next值為0,第二位的next值為1,後面求解每一位的next值時,根據前一位進行比較。首先將前一位與其next值對應的內容進行比較,如果相等,則該位的next值就是前一位的next值加上1;如果不等,向前繼續尋找next值對應的內容來與前一位進行比較,直到找到某個位上內容的next
簡單講解KMP單模式匹配與AC演算法多模式匹配(KMP篇)
前言 本篇是對於KMP單模式匹配以及AC演算法多模式匹配的簡單講解,KMP演算法與AC演算法是關鍵字檢索中的常見演算法,能夠快速而高效地查找出目標字串中的多個關鍵字的匹配情況,而要檢索的關鍵字通常被稱為模式串,因此模式匹配四個字也就好理解了。網上的很多對於KMP的講解總是結
字串模式匹配中BF演算法和KMP演算法的java實現
關於BF演算法和KMP演算法的具體解釋,文章【部落格地址】:KMP字串匹配演算法與next陣列中有推薦部落格的具體地址,可以在這些部落格中找到詳細的解釋。 以下只有具體的java程式碼實現: BF演
【演算法】KMP演算法
# 簡介 KMP演算法由 `Knuth-Morris-Pratt` 三位科學家提出,可用於在一個 `文字串` 中尋找某 `模式串` 存在的位置。 本演算法可以有效降低在一個 `文字串` 中尋找某 `模式串` 過程的時間複雜度。(如果採取樸素的想法則複雜度是 $O(MN)$ ) 題面:https://www
【圖片匹配】--- SIFT_Opencv3.1.0_C++_ubuntu
文件 read 等待 s2d imread mage clas create detect 最近在搗鼓圖片相似性匹配算法。這裏先說一點必要的題外話: 如果是在同一個object不同角度拍攝的多張圖片中,使用SIFT可以有不錯的效果; 如果是尋找類別相同的圖片(可能不是同
PHP PC端微信掃碼支付【模式二】詳細教程-附帶源碼(轉)
idt class pid 方法 按鈕 -c 商戶 開源 玩意兒 博主寫這破玩意兒的時候花了大概快兩天時間才整體的弄懂邏輯,考慮了一下~還是把所有代碼都放出來給大家~抱著開源大無私的精神!誰叫我擅長拍黃片呢?同時也感謝我剛入行時候那些無私幫過我的程序員們! 首先還是
CF 612C. Replace To Make Regular Bracket Sequence【括號匹配】
pos cal set while ostream problem \n push || 【鏈接】:CF 【題意】:給你一個只含有括號的字符串,你可以將一種類型的左括號改成另外一種類型,右括號改成另外一種右括號 問你最少修改多少次,才能使得這個字符串匹配,輸出次數 【分析】
【詳解】KMP算法
是不是 代碼 ++ 大牛 bilibili 開始 最長 [] 分別是 前言 KMP算法是學習數據結構 中的一大難點,不是說它有多難,而是它這個東西真的很難理解(反正我是這麽感覺的,這兩天我一直在研究KMP算法,總算感覺比較理解了這套算法, 在這裏我將自己的思路分享給大家
