先瞎扯幾句

樹上倍增的經典應用是求兩個節點的LCA

當然它的作用不僅限於求LCA，還可以維護節點的很多資訊

求LCA的方法除了倍增之外，還有樹鏈剖分、離線tarjan ，這兩種日後再講（眾人：其實是你不會吧:unamused:。。。）

思想

樹上倍增嘛，顧名思義就是倍增

相信倍增大家都不預設，著名的rmq問題的$O(n*logn)$的解法就是利用倍增實現的

在樹上倍增中，我們用

$f[j][i]$表示第$j$號節點，跳了$2^j$步所能到達的節點

$deep[i]$表示$i$號節點的深度

然後用這兩個陣列瞎搞搞就能整出LCA來啦

眾人：:wrench:  :hammer: :hocho:

實現

deep&&f[i][0]

首先，$f[i][0]$(也就是一個節點的上面的節點)容易求得，只要對整棵樹進行一邊dfs就好，在dfs的時候我們順便可以求出$deep$陣列

for(int i=head[now];i!=-1;i=edge[i].nxt)
        if(!deep[edge[i].v])
            deep[edge[i].v]=deep[now]+1,f[edge[i].v][0]=now,dfs(edge[i].v);

這段程式碼應該不難理解

f[j][i]

那麼我們怎麼維護$f$陣列呢？

不難得到$f[j][i]=f[f[j][i-1]][i-1]$ 眾人：難！

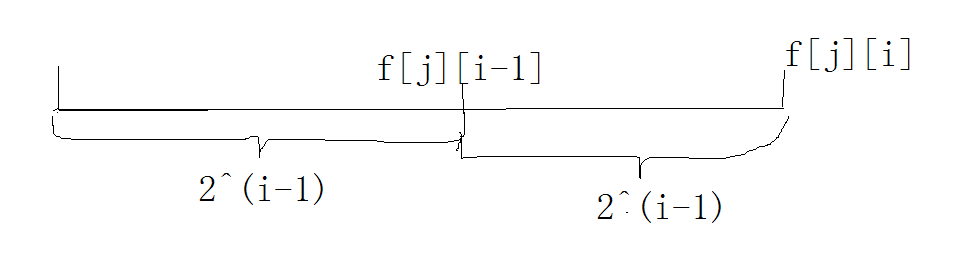
其實真的不難，一張圖就可以解釋明白啦

這句話的意思其實是說，一個節點跳$2^j$所能到達的節點實際上是跳$2^{i-1}$所能到達的節點再往上跳$2^{j-1}$步

注意$2^i=2^{i-1}+2^{i-1}$

程式碼：

for(int i=1;i<=19;i++)    
    for(int j=1;j<=n;j++)
        f[j][i]=f[f[j][i-1]][i-1];

LCA

接下來要進入最核心的部分啦，

我們如何用$deep$和$f$亂搞搞出$x$和$y$的LCA呢？

按照書上倍增演算法的介紹

我們求LCA需要分為兩步

設$deep[x]>deep[y]$

1. 讓$x$向上跳，跳到與$y$深度相同位置
2. 讓$x$和$y$同時向上跳，跳到祖先相同位置

根據二進位制分解什麼亂七八糟的，這麼做一定是對的，其實這個挺顯然的，yy一下就好了吧。。。

第一步

if(deep[x]<deep[y])    swap(x,y);
    for(int i=19;i>=0;i--)
        if(deep[f[x][i]]>=deep[y])
            x=f[x][i];

首先處理一下$x$和$y$的深度，保證$deep[x]>deep[y]$

然後儘量讓$x$向上跳就好啦，注意這裡是可以取到等號的

注意這裡可能會出現一種特殊情況

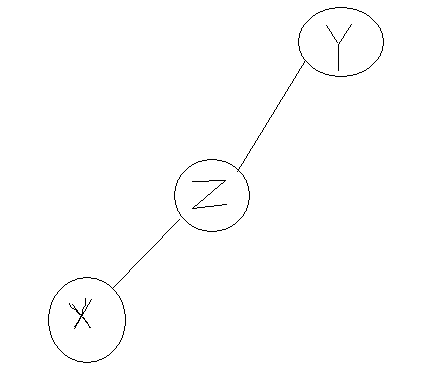
這個時候他們的最近公共祖先就是$y$

if(x==y)    return x;

 第二步

同時向上跳，直到祖先相同為止

那麼此時他們再向上跳一步所能到達的節點就是LCA啦

for(int i=19;i>=0;i--)
    if(f[x][i]!=f[y][i])
        x=f[x][i],y=f[y][i];
return    f[x][0];

怎麼樣？

是不是很簡單？

完整程式碼

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN=1000010;
inline void read(int &n)
{
    char c=getchar();bool flag=0;n=0;
    while(c<'0'||c>'9')    c=='-'?flag=1,c=getchar():c=getchar();
    while(c>='0'&&c<='9')    n=n*10+c-48,c=getchar();flag==1?n=-n:n=n;
}
struct node
{
    int v,nxt;
}edge[MAXN];
int head[MAXN];
int num=1;
inline void add_edge(int x,int y)
{
    edge[num].v=y;
    edge[num].nxt=head[x];
    head[x]=num++;
}
int f[MAXN][21];
int deep[MAXN];
int n,m,root;
void dfs(int now)
{
    for(int i=head[now];i!=-1;i=edge[i].nxt)
        if(!deep[edge[i].v])
            deep[edge[i].v]=deep[now]+1,f[edge[i].v][0]=now,dfs(edge[i].v);
}
void PRE()
{
    for(int i=1;i<=19;i++)    
        for(int j=1;j<=n;j++)
            f[j][i]=f[f[j][i-1]][i-1];
} 
int LCA(int x,int y)
{
    if(deep[x]<deep[y])    swap(x,y);
    for(int i=19;i>=0;i--)
        if(deep[f[x][i]]>=deep[y])
            x=f[x][i];
    if(x==y)    return x;
    for(int i=19;i>=0;i--)
        if(f[x][i]!=f[y][i])
            x=f[x][i],y=f[y][i];
    return    f[x][0];
}
int main()
{
    
    memset(head,-1,sizeof(head));
    read(n);read(m);read(root);
    for(int i=1;i<=n-1;i++)
    {
        int x,y;read(x);read(y);
        add_edge(x,y);
        add_edge(y,x);
    }
    deep[root]=1;
    dfs(root);
    PRE();
    for(int i=1;i<=m;i++)
    {
        int x,y;
        read(x);read(y);
        printf("%d\n",LCA(x,y));
    }
    return 0;
} 

例題

都是些入門難度的題目

http://www.cnblogs.com/zwfymqz/p/6832524.html

http://www.cnblogs.com/zwfymqz/p/7791527.html

http://www.cnblogs.com/zwfymqz/p/7791617.html

http://www.cnblogs.com/zwfymqz/p/7791517.html