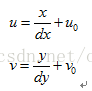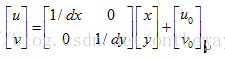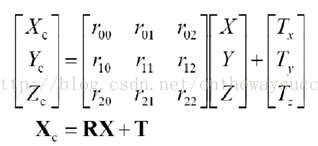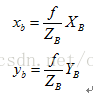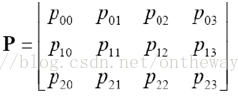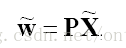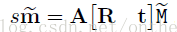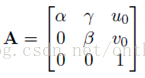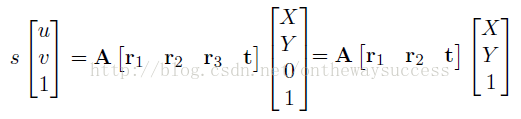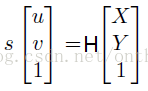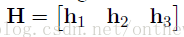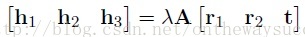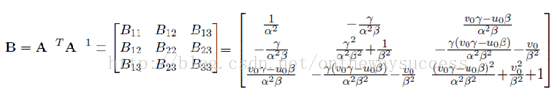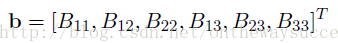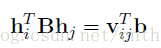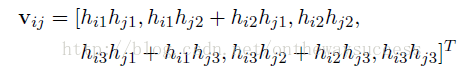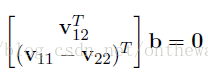玉米竭力用輕鬆具體的描述來講述雙目三維重建中的一些數學問題。希望這樣的方式讓大家以一個輕鬆的心態閱讀玉米的《計算機視覺學習筆記》雙目視覺數學架構系列部落格。這個系列部落格旨在捋順一下已標定的雙目視覺中的數學主線。數學推導是有著幾分枯燥的，但奇妙的計算機視覺世界是建立在嚴密的數學架構之上的。所以對數學框架的理解是理解雙目視覺的必由之路。不過請大家放心，接下來玉米會以儘量有趣，儘量更接地氣兒的方式，闡釋一下自己對雙目視覺數學或者說是投影幾何的理解。

       先來張《計算機視覺：演算法與應用》中的3D重建示例圖鎮樓！

         好吧，現在言歸正傳，來看看幾何學上世界是怎樣投影進攝相機裡的吧！接下來讓我們來看一下本系列部落格的第一“搏”：

影象座標：我想和世界座標談談(A)

首先，我先解釋一下這個題目吧。題目的字面意義是說：影象座標系想和世界座標系談談。這裡麵包含著兩個問題：

         A、談話物件：視覺系統的三大座標系：世界座標系，攝像機座標系和影象座標系。這是玉米在本文《我想和世界座標談談 (A)》中想要和大家分享的內容。其中主要包含：三大座標系的位置、作用和應用場景。

         B、談話方式：兩個不同的座標系之間該如何溝通呢？玉米將在《我想和世界座標談談(B)》中和大家分享一下剛體變換和透視                 投影變換。連起兩個座標系之間這不在一個參考系的“世界上最遠的距離”。

好吧，下面讓我們來揭開三大座標系的廬山真面目。

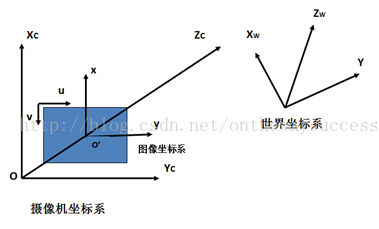
         上圖是三個座標的示意簡圖，通過它大家可以對三個座標有一個直觀的認識。下面來看看三個座標系的骨子裡藏了什麼。

         世界座標系（X_W,Y_W,Z_W）：其是目標物體位置的參考系。除了無窮遠，世界座標可以根據運算方便與否自由放置。在雙目視覺中世界座標系主要有三個用途：1、標定時確定標定物的位置2、作為雙目視覺的系統參考系，給出兩個攝像機相對世界座標系的關係，從而求出相機之間的相對關係3、作為重建得到三維座標的容器，盛放重建後的物體的三維座標。世界座標系是將看見中物體納入運算的第一站。

        攝像機座標系(X_C,Y_C,Z_C)：其是攝像機站在自己角度上衡量的物體的座標系。攝像機座標系的原點在攝像機的光心上，z軸與攝像機光軸平行。

它是與拍攝物體發生聯絡的橋頭堡，世界座標系下的物體需先經歷剛體變化轉到攝像機座標系（旋轉和平移），然後再和影象座標系發生關係。它是影象座標與世界座標之間發生關係的紐帶，溝通了世界上最遠的距離。哈哈

         影象座標系(x,y)米/(u,v)畫素 :其是以攝像機拍攝的二維照片為基準建立的座標系。用於指定物體在照片中的位置。玉米更傾向將(x,y)稱為連續影象座標或空間影象座標，將(u,v)稱為離散影象座標系或者是畫素影象座標系（雖然這樣的稱呼未經考證，但更能傳達二者的物理意義）。

          (x,y)座標系的原點位於攝像機光軸與成像平面的焦點O’(u0,v0)上，單位為長度單位(米)。(u,v)座標系的原點在圖片的左上角（其實是儲存器的首地址）如上圖所示，單位為數量單位(個)。(x,y)主要用於表徵物體從攝像機座標系向影象座標系的透視投影關係。而(u,v)則是實實在在的，我們能從攝像機中得到的真實資訊。

(x,y)與(u,v)存在如下轉換關係：

          dx代表x軸方向一個畫素的寬度，dy代表y軸方向上一個畫素的寬度。dx、dy為攝像機的內參數。(u0,v0)稱為影象平面的主點，也是攝像機的內參數。其實相當於對x軸和y軸的離散化。其可以運用齊次座標，將上式寫成矩陣形式，如下：

 

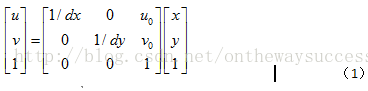
      （1）式運用了齊次座標，初學者可能會感到有些迷惑。大家會問：怎樣將普通座標轉換為齊次座標呢？齊次座標能帶來什麼好處呢？

         玉米在這裡對齊次座標做一個通俗的解釋。此處只講怎麼將普通座標改寫為齊次座標及為什麼引入齊次座標。這裡只做一個通俗但不太嚴謹的表述。力求簡單明瞭。針對齊次座標的嚴謹的純數學推導，可參見“周興和版的《高等幾何》---1.3拓廣平面上的齊次座標”。玉米曾詳細讀過《高等幾何》這本書，但覺得離計算機視覺有點遠，是講純數學的投影關係的，較為生澀難懂。

        齊次座標可以理解為在原有座標後面加一個“小尾巴”。將普通座標轉換為齊次座標，通常就是在增加一個維度，這個維度上的數值為1。如影象座標系(u,v)轉換為(u,v,1)一樣。對於無窮遠點，小尾巴為0。注意，給零向量增加小尾巴，數學上無意義。

那麼，為什麼計算機視覺在座標運算時要加上這個“小尾巴”呢？

        玉米看來有兩點原因：

         1、 將投影平面擴充套件到無窮遠點。如對消隱點(vanishing point)的描述。

          2、 使得計算更加規整

         如式（1）如果用普通座標來表達的話，會是下面的樣子：

這樣的運算形式會給後與運算帶來一定的麻煩，所以齊次座標是一個更好的選擇。

          齊次座標還有一個重要的性質，伸縮不變性。即：設齊次座標M，則αM=M。

玉米才疏學淺，筆記中如有紕漏指出，希望大家不吝指出。玉米在這裡拜謝啦！

二、影象座標：我想和世界座標談談(B)

         玉米將在這篇博文中，對影象座標與世界座標的這場對話中涉及的第二個問題：談話方式，進行總結。世界座標是怎樣變換進攝像機，投影成影象座標的呢？

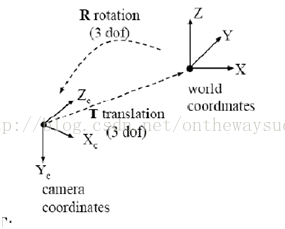
        玉米做了一個簡單的圖示，在這裡做一個提綱。圖中顯示，世界座標系通過剛體變換到達攝像機座標系，然後攝像機座標系通過透視投影變換到達影象座標系。可以看出，世界座標與影象座標的關係建立在剛體變換和透視投影變換的基礎上。為了獎勵剛體變和透視投影變換溝通了“世界上最遠的距離”，玉米在圖上獎勵了他們兩朵小紅花。哈哈

        首先，讓我們來看一下剛體變換是如何將世界座標系與影象座標系聯絡起來的吧。這裡，先對剛體變換做一個介紹：

        剛體變換(regidbody motion):三維空間中， 當物體不發生形變時，對一個幾何物體作旋轉， 平移的運動，稱之為剛體變換。

因為世界座標系和攝像機座標都是右手座標系，所以其不會發生形變。我們想把世界座標系下的座標轉換到攝像機座標下的座標，如下圖所示，可以通過剛體變換的方式。空間中一個座標系，總可以通過剛體變換轉換到另外一個個座標系的。轉一轉，走一走，就到另外一個座標系下了。以前可能是面朝大海，經過平移旋轉，最終可能只能面朝冰山了，哈哈

         下面讓我來看一下，二者之間剛體變化的數學表達。

         其中，X_C代表攝像機座標系，X代表世界座標系。R代表旋轉，T代表平移。R、T與攝像機無關，所以稱這兩個引數為攝像機的外引數(extrinsic parameter)可以理解為兩個座標原點之間的距離，因其受x,y,z三個方向上的分量共同控制，所以其具有三個自由度。

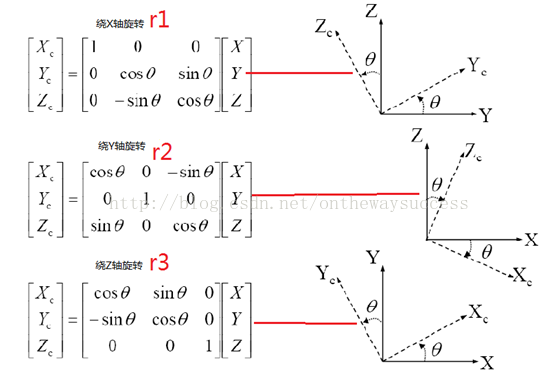
         R則為分別繞XYZ三軸旋轉的效果之和。如下面所示：

         R=r1*r2*r3.其由三個方向的θ控制，故具有三個自由度。

   好了，剛體變換就講完了。大家應該都瞭解，世界座標系到攝像機座標系之間的轉換過程了吧。

          接下來，讓我們看看攝像機座標下的座標如何投影到影象座標系下，最終變為照片中的一個畫素。這其中包含兩個過程：一是從攝像機座標到“空間影象座標”（x,y）所發生的透視投影；二是從“連續影象座標”到“離散影象座標”(u,v)。後者我們已經在第一篇博文中解釋過。所以在這裡，主要介紹一下透視投影。

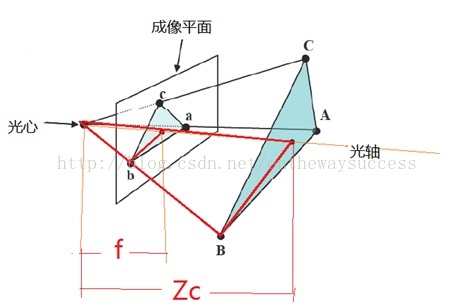
透視投影(perspective projection): 用中心投影法將形體投射到投影面上，從而獲得的一種較為接近視覺效果的單面投影圖。有一點像皮影戲。它符合人們心理習慣，即離視點近的物體大，離視點遠的物體小，不平行於成像平面的平行線會相交於消隱點(vanish point)。

         囉嗦這麼多，其實大家看看示意圖，看看公式，秒懂。

         以圖中B(X_B,Y_B)點為例，在小孔成像攝像機模型下（幾何分析的最常用模型）。這裡的f為攝像機的焦距，其屬於攝像機的內參數(intrinsic parameter)。其在成像平面上的投影點b(x_b,y_b)的座標利用簡單的相似三角形比例關係很容易求出：

         上面兩式也闡明瞭攝像機座標與影象座標之間的透視投影關係。

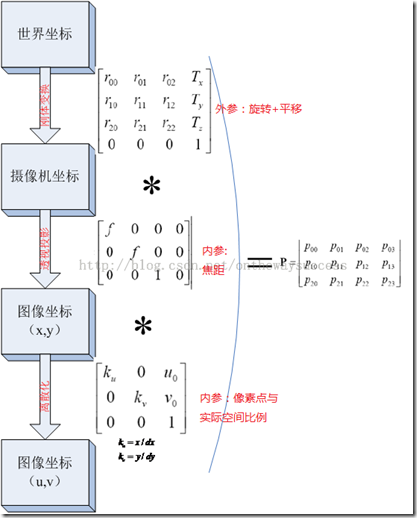
好吧，現在玉米已經把影象座標與世界座標之間的這場對話所需經歷的三個波折的過程加以瞭解釋。即：剛體變換、透視投影、(x,y)換(u,v)（ps.這個在上一篇博文中講過）。接下來玉米用一張圖把三個過程連線起來。實現從世界座標(X,Y,Z)到(u,v)之間的轉換。讓影象座標與世界座標直接對話。

         下圖中的轉換關係，都是用齊次座標表達的，大家會發現這樣的表達非常整潔。

         其實這張圖顯示的過程還有一個名字：攝像機模型(camera model)。其實也就是攝像機的幾何模型了。

         將三者相乘，可以把這三個過程和在一起，寫成一個矩陣：

         P就是世界座標到影象座標的直接聯絡人，P就表示了一個投影相機，有下面公式：

         注意在表示齊次座標時，需要在符號上面加個小帽子。除去齊次座標控制位P_23，P具有11個自由度。

        攝像機模型及其中涉及的座標系等，是弄清3D重建幾何框架的基礎。可以把它們視為基本運算關係。後面對於三維重建幾何框架的推導，都是要用到三個基本座標系和攝像機模型的。

         到這裡玉米就順利搭建起了影象座標與世界座標間的這場對話。如有紕漏還請大家擔待，並指正！

三、致敬“張正友標定”

         此處“張正友標定”又稱“張氏標定”，是指張正友教授於1998年提出的單平面棋盤格的攝像機標定方法。張氏標定法已經作為工具箱或封裝好的函式被廣泛應用。張氏標定的原文為“A Flexible New Technique forCamera Calibration”。此文中所提到的方法，為相機標定提供了很大便利，並且具有很高的精度。從此標定可以不需要特殊的標定物，只需要一張打印出來的棋盤格。So great! 這樣的方法讓人肅然起敬。所以玉米的這篇部落格的題目是：致敬“張氏標定”。

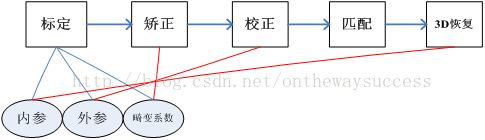
         當然，此博的內容也是圍繞著“張氏標定”進行的，在這裡，玉米主要介紹一下，“張氏標定”的數學思路。因為標定在整個基於標定攝像機的三維重建的幾何過程佔有最重要最核心的地位。如下圖：

         從圖中明顯可以看出，標定得到的內參、外參和畸變係數，是雙目視覺進行圖片矯正，攝像機校正和3D恢復的基礎。沒有好的標定，雙目視覺系統就無法完成3D重建。

        既然標定對雙目視覺如此重要，我們有必要對數學的深層含義多加理解。以張氏標定為例，讓我們挖開工具箱，看看其數學本質吧。因為張教授的論文中對標定方法的講述是循序漸進的，所以玉米在這裡將按照張教授論文中的順序，為大家講述一下，張氏標定的脈絡。

1、標定平面到影象平面的單應性

        因為張氏標定是一種基於平面棋盤格的標定，所以想要搞懂張氏標定，首先應該從兩個平面的單應性(homography)對映開始著手。

        單應性(homography)：在計算機視覺中被定義為一個平面到另一個平面的投影對映。首先看一下，影象平面與標定物棋盤格平面的單應性。

        由上兩篇博文中講到的攝像機模型，肯容易得到：

         其中m的齊次座標表示影象平面的畫素座標(u,v,1)，M的齊次座標表示世界座標系的座標點(X,Y,Z,1)。A[R t]即是上面一篇部落格推出的P。R表示旋轉矩陣、t表示平移矩陣、S表示尺度因子。A表示攝像機的內參數,具體表達式如下：

α=f/dx，β=f/dy,因為畫素不是規規矩矩的正方形，γ代表畫素點在x,y方向上尺度的偏差。

         這裡還有一個“梗兒”，就是S。它只是為了方便運算，對於齊次座標，尺度因子不會改變座標值的。

因為標定物是平面，所以我們可以把世界座標系構造在Z=0的平面上。然後進行單應性計算。令Z=0可以將上式轉換為如下形式：

         既然，此變化屬於單應性變化。那麼我們可以給A[r1 r2 t]一個名字：單應性矩陣。並記H= A[r1 r2 t]。

         那麼現在就有：

         大家可以分析一下，H是一個三3*3的矩陣，並且有一個元素是作為齊次座標。因此，H有8個未知量待解。

(x,y)作為標定物的座標，可以由設計者人為控制，是已知量。(u,v)是畫素座標，我們可以直接通過攝像機獲得。對於一組對應的(x,y)-à(u,v)我們可以獲得兩組方程。

        現在有8個未知量需要求解，所以我們至少需要八個方程。所以需要四個對應點。四點即可算出，影象平面到世界平面的單應性矩陣H。

        這也是張氏標定採用四個角點的棋盤格作為標定物的一個原因。

        在這裡，我們可以將單應性矩陣寫成三個列向量的形式，即：

2、利用約束條件求解內參矩陣A

        從上面可知，應用4個點我們可以獲得單應性矩陣H。但是，H是內參陣和外參陣的合體。我們想要最終分別獲得內參和外參。所以需要想個辦法，先把內參求出來。然後外參也就隨之解出了。我們可以仔細的“觀摩”一下下面的式子。

       從中可以得出下面兩個約束條件，這兩個約束條件都是圍繞著旋轉向量來的。

       1、r1,r2正交 得：r1r2=0。這個很容易理解，因為r1,r2分別是繞x,y軸旋轉的。應用高中立體幾何中的兩垂直平面上（兩個旋轉向量分別位於y-z和x-z平面）直線的垂直關係即可輕鬆推出。

        2、旋轉向量的模為1，即|r1|=|r2|=1。這個也很容易理解，因為旋轉不改變尺度嘛。如果不信可以回到上一篇部落格，找到個方向的旋轉矩陣化行列式算一下。

        通過上面的式子可以將r1,r2代換為h1,h2與A的組合進行表達。即       r1=h1A^-1，r2=h2A^-1.根據兩約束條件，可以得到下面兩個式子：

        大家從上面兩個式子是不是看出一點端倪了。式子中，h1,h2是通過單應性求解出來的那麼未知量就僅僅剩下，內參矩陣A了。內參陣A包含5個引數：α，β，u0，v0，γ。那麼如果我們想完全解出這五個未知量，則需要3個單應性矩陣。3個單應性矩陣在2個約束下可以產生6個方程。這樣可以解出全部的五個內參了。大家想一下，我們怎樣才能獲得三個不同的單應性矩陣呢？答案就是，用三幅標定物平面的照片。我們可以通過改變攝像機與標定板間的相對位置來獲得三張不同的照片。（當然也可以用兩張照片，但這樣的話就要捨棄掉一個內參了γ=0）

       到這裡，大家應該就明白我們在張氏標定法時為什麼要不斷變換標定板的方位了吧。當然這只是一個原因。第二個原因，玉米會在講極大似然時講到。

       下面在對我們得到的方程做一些數學上的變化，這些變化都是簡單的運算變化了，相信大家動動筆，一算就可以算出。這些變化都是為了運算方便的，所以也沒什麼物理意義。

首先令：

        很容易發現B是一個對稱陣，所以B的有效元素只剩下六個（因為有三對對稱的元素是相等的，所以只要解得下面的6個元素就可以得到完整的B了），讓這六個元素構成向量b。

        接下來在做一步純數學化簡：

        可以計算得：

         利用約束條件可以得到下面，方程組：

          這個方程組的本質和前面那兩個用h和A組成的約束條件方程組是一樣的。在此重複一遍解釋：如果我們想完全解出這五個未知量，則需要3個單應性矩陣。3個單應性矩陣在2個約束下可以產生6個方程。這樣可以解出全部的五個內參了。大家想一下，我們怎樣才能獲得三個不同的單應性矩陣呢？答案就是，用三幅標定物平面的照片。我們可以通過改變攝像機與標定板間的相對位置來獲得三張不同的照片。（當然也可以用兩張照片，但這樣的話就要捨棄掉一個內參了γ=0）

       通過至少含一個棋盤格的三幅影象，應用上述公式我們就可以估算出B了。得到B後，我們通過cholesky分解 ，就可以輕鬆地得到攝像機的內參陣A。

3、基於內參陣估算外參陣

相關推薦