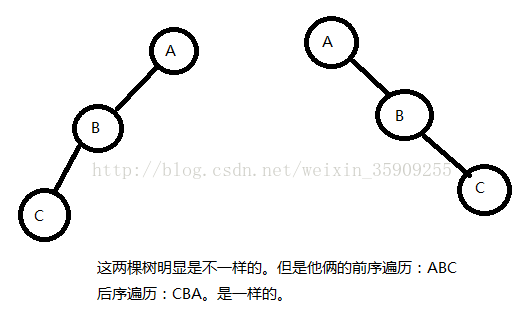
資料結構的基礎知識中重要的一點就是能否根據兩種不同遍歷序列的組合（有三種：先序+中序，先序+後序，中序+後序），唯一的確定一棵二叉樹。然後就是根據二叉樹的不同遍歷序列（先序、中序、後序），重構二叉樹。顯然，這三種組合並不是都能唯一確定二叉樹的，其中先序+後序就不能唯一確定一棵二叉樹。這裡我就不證明了。舉個反例：

反例：任何結點只有左子樹的二叉樹和任何結點只有右子樹的二叉樹，其前序序列相同，後序序列相同，但卻是兩棵不同的二叉樹。

2、構造思路：

（1）根據先序遍歷序列和中序遍歷序列構建二叉樹：
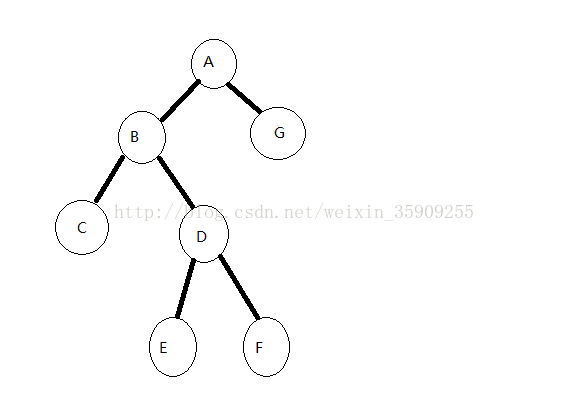
先序：ABCDEFG

中序：CBEDFAG

step1、先序遍歷的第一個結點總是根結點。如上圖中的二叉樹，根結點為A，也是先序遍歷的第一個值。先序遍歷時父親結點總是在孩子結點之前遍歷。

step2、可以觀察到在中序遍歷中，A是第5個值（從0開始算起）。由於中序遍歷順序為：左子樹，根結點，右子樹。所以A左邊的{CBEDF} 這四個結點屬於左子樹，而根結點A右邊的{G}屬於右子樹。

step3、可以從上面的結論很輕鬆的得到遞迴式。在構建了根結點A後，我們可以根據中序遍歷{CBEDF} 和{G}分別構建它的左子樹和右子樹。我們同時需要相應的先序遍歷結果用於發現規律。我們可以由先序遍歷知道左右子樹的先序遍歷分別是{CBEDF}和{G}。左右子樹也分別為二叉樹，由此可以遞迴來解決問題。

補充進我之前寫的二叉樹類中（class BinTree）

int Creat_VLR_LVR(T VLR[],T LVR[],int len)
	{
		return Creat_VLR_LVR(root,VLR,VLR+len-1,LVR,LVR+len-1);
	}
 

//VLR：根左右---------------前序遍歷
	//LVR：左根右---------------中序遍歷
	int Creat_VLR_LVR(BinTreeNode<T> *&p,T *VLRh,T *VLRt,T *LVRh,T *LVRt)//////////////////////////////////////////////////////////////////////
	{
		T *valuepre = VLRh;//先取出前序遍歷的第一個值來作為根節點
		T *valuein = LVRh;   //去中序陣列的指標
		p = new BinTreeNode<T>((*valuepre));
		if(*VLRh == *VLRt||*LVRh == *LVRt)
		{
			return OK;
		}
		if(*valuepre == '\0'&&*valuein == '\0')
		{
			return OK;
		}
		while((*valuein) != '\0'&& (*valuein) != *valuepre)
			++valuein;
		int leftlen = valuein - LVRh;
		T *leftVLR = VLRh + leftlen;
		if(leftlen > 0)
		{
			Creat_VLR_LVR(p->left,VLRh+1,VLRt,LVRh,valuein-1);
		}
		if(leftlen < VLRt-VLRh)
		{
			Creat_VLR_LVR(p->right,leftVLR+1,VLRt,valuein+1,LVRt);
		}
		return OK;
	}
 

（2）根後序遍歷序列和中序遍歷序列構建二叉樹：
後序：CEFDBGA

中序：CBEDFAG

step1、後序遍歷的最後一個結點總是“根結點”。如上圖中的二叉樹，根結點為A，也是後序遍歷的最後一個值。

step2、在中序遍歷中找到“根節點”，但是這裡要先建立右子樹，因為後序遍歷後面的是右子樹的根節點，（這裡唯一跟前序遍歷不一樣的是後序遍歷是從後往前一個一個退的）。從中序遍歷中我們可以看到{G}是A的右子樹，所以先建立。

step3、後序遍歷再往前退，到B，那麼B是A的左子樹......

根據以上的結論，通過遞迴好實現的。

	int Creat_LRV_LVR(T LRV[],T LVR[],int len)
	{
		return Creat_LRV_LVR(root,LRV,LRV+len-1,LVR,LVR+len-1);
	}

	//LRV：左右根---------------後序遍歷
	//LVR：左根右---------------中序遍歷
	int Creat_LRV_LVR(BinTreeNode<T> *&p,T *LRVh,T *LRVt,T *LVRh,T *LVRt)
	{
		T *valuepost = LRVt;
		T *valuein = LVRh;
		p = new BinTreeNode<T>((*valuepost));
		if(*LRVh == *LRVt||*LVRh == *LVRt)
			return OK;
		if(*valuein == '\0')
			return OK;
		while((*valuein) != '\0'&& (*valuein) != *valuepost)
			++valuein;
		int rightlen = LVRt-valuein; //中序遍歷右子樹的長度
		T *rightLRV = LRVt - rightlen;//後序遍歷
		if(rightlen > 0)
		{
			Creat_LRV_LVR(p->right,LRVh,LRVt-1,valuein+1,LVRt);//除錯的時候要注意看好這裡的引數
		}
		if(rightlen < LRVt-LRVh)
		{
			Creat_LRV_LVR(p->left,LRVh,LRVt-rightlen-1,LVRh,valuein-1);//除錯的時候要注意看好這裡的引數
		}
		return OK;
	}