分類：決策樹——樹的生長
分類算法非常適合預測或描述標簽為二元或標稱類型的數據集，對於標簽為序數類型的數據集，分類技術則不太有效，因為分類技術不考慮隱藏在序數中的“序”關系，對於標簽其他形式的聯系如子類與超類（包含的關系），分類技術也不太適合。
本文是分類模型系列的初篇，先介紹最基本的分類/回歸模型——決策樹模型。決策樹分類模型打算分為三篇來說明，第一篇先說明決策樹生長，第二篇介紹決策樹的剪枝過程，第三篇介紹常用的決策樹模型算法。
1.樹的生長過程
決策樹的生長一般采用貪心的策略，所有訓練樣本都會參與到樹的生長過程，樹生長完成後所有訓練樣本都能被明確的分類。訓練集 中
表示各樣本的屬性值，
的標簽，
表示樣本的屬性集，則決策樹的構建方法如下
- 生成結點node
- 若D中所有樣本均屬於同一類別C，則將結點node標記為葉結點，其類歸為類C，返回
- 若A為空、或者D中樣本在A中屬性上取值相同， 則將結點node記為葉節點，其類歸為D中樣本數最多的類，返回
- 若2、3中情況均未出現時，從A中選擇一個最優劃分屬性
，對
表示
在
時的樣本子集
- 若
（從
中去掉
在樹的生長步驟4中，提到了“選擇一個最優的劃分屬性”、“
的每一個劃分值”問題，那麽該如何選擇最優劃分屬性、劃分值呢？
2.樹生長過程中需要考慮的問題
正如第1節中提到的問題，在每一個內部結點上，如何選擇最優劃分屬性、劃分值呢？這正是需要考慮的問題。
2.1最優屬性的度量參數
優劣的比較應該是有一個量化的評判標準的，在最優屬性的抉擇上，一般采用“信息增益”、“增益率”、“基尼指數”這三個參數中的一個來評判。最優屬性指的是利用該屬性劃分結點上數據後，信息增益/增益率/基尼指數 變化最大。下面以離散取值屬性為例，分別介紹這幾個參數
- 信息增益
“信息熵”在信息論中表示隨機變量不確定性程度，用於樣本集合中，則可以用來度量集合的純度，也即是表征集合中樣本類別數量、每中類別對應樣本數量的信息。
信息熵定義如下
(1)
式(1)中為樣本集
中第
類樣本數占總樣本數的比例，信息熵值越小，表示樣本數據集純度越高，當所有樣本屬於同一類時，純度最高，為0。特別的，規定當
時，
對於離散取值屬性a，其取值範圍為，若將內部節點node按屬性a進行子女結點劃分，則其樣本數據集D被劃分為
，則對結點node進行劃分後，其信息增益
定義為
(2)
式(2)中表示樣本集
中樣本數，
表示樣本集
中樣本數。一般而言，信息增益
越大，表示按照屬性a劃分後樣本數據的純度提升越大。對於取連續值的屬性a，一般也是將其取值離散化。
-
增益率
當屬性的取值數目較多時，信息增益計算結果會偏大一些，因為更多的葉子結點必然能達到更低的誤分類率，信息增益也就越小。為了減小這種情況帶來的不利影響，提出了增益率，其定義為
(3)
式(3)中定義為
(4)
當屬性的取值數目較少時，在式(3)的增益率計算結果又會偏大一些。基於此，綜合考慮之後Quinlan教授提出了這樣一個依據增益率選擇劃分屬性的方法：先從待劃分屬性中找出信息增益高出平均水平的屬性，然後再從這些信息增益結果中選擇增益率最高的屬性作為最終的劃分屬性。
-
基尼指數
基尼指數實際上是經濟學中的概念，用來衡量財富分配的不均衡性，也可以依據該指數來選擇劃分屬性。首先對基尼值做如下定義
(5)
式(5)中定義與式(1)中一致。對於
，可以這樣解釋，從樣本數據集D中隨機抽取一個樣本，該樣本屬於類
的概率。因此，基尼系數可以直觀的解釋為：隨機從數據集D中抽取兩個樣本，這兩個樣本所屬類不一致的概率，該概率越小，表明數據集D的純度越高。基於基尼值，基尼指數
的定義如下
(6)
依據基尼指數選擇劃分屬性時，選擇基尼指數最小的屬性。
2.2 連續型屬性的劃分值
在2.1節中，都是以離散取值型屬性為例來定義信息增益、增益率、基尼指數，對於連續取值型屬性，需先對其離散化，實際上對於連續型屬性，采樣後得到的樣本的屬性值已經是離散的，不過在選擇劃分值時，還要考慮訓練樣本中未出現的值。
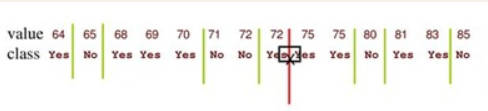
對給定的樣本集D和連續型劃分屬性a，將D中屬性a的取值從小到大排列，得到，對該集合中任意兩個相鄰取值
、
，劃分值取它們之間任意一個值時，對D來說都不影響劃分結果，因此一般取二者平均值即可
這樣就得到屬性a新的劃分值集合，接著可以按照第2.1節中的方法來判斷屬性a是否為最佳劃分屬性。在計算劃分值時，有一個小竅門可以註意一下，當將樣本集D中屬性a的取值從小到大順序排列之後，若有一段相鄰的樣本類別相同，則集合
中由這一段相鄰樣本計算出的值可以不予以考慮，有時候這樣可以減少許多計算量。
?
事實上不僅在連續型屬性的劃分值上需要處理，一些算法中要求決策樹是二叉樹，此時包括多個取值的離散型屬性在內，劃分值都需要單獨處理。這個部分放在特定的算法中說明（決策樹系列的第三篇）
3 樹生長的終止條件
第1節中描述決策樹的生長過程是一個“完全”的生長過程，生長的終止條件為：所有的樣本屬於同一類，或者所有的樣本具有相同的屬性值。從目前應用較廣的決策樹模型來看，這種“完全”式的生長過程是合理的，它能較小訓練誤差，但要得到一棵泛化誤差較小的樹，還需要進行剪枝處理，這將在下一篇《分類：決策樹——剪枝》中說明。
分類：決策樹——樹的生長