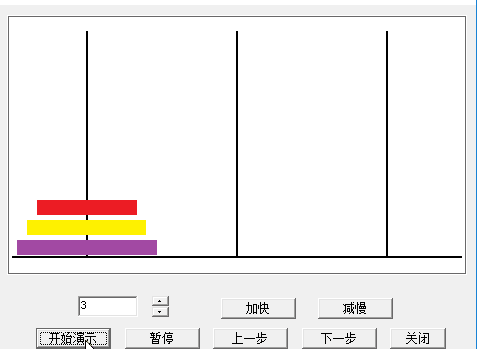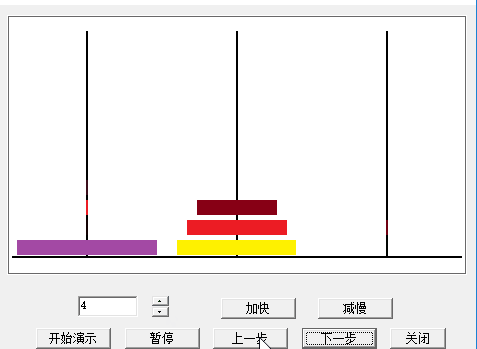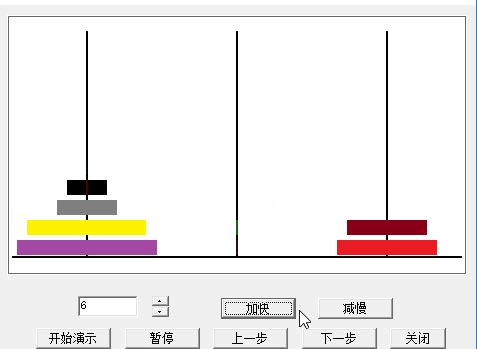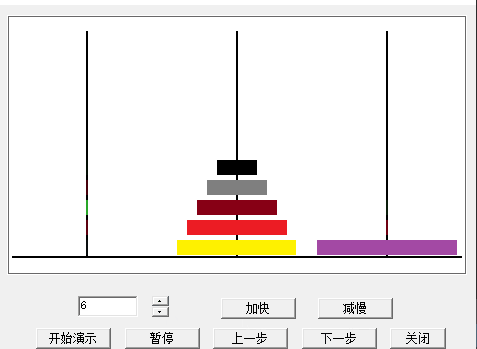
首先展示一下程式演示效果：

一、程式功能：

1、可演示盤數為2-7時，移動步驟

2、點選spin按鈕可增或減盤子的個數，也可在編輯框內輸入數字，數字必須在3-7之間

3、可連續移動盤子，也可在中間暫停，對應的按鈕為“開始演示”和“暫停”

4、可單步演示盤子的移動，對應的按鈕為“上一步”與“下一步”

二、基本思路：

傳統的漢諾塔程式採用的是遞迴程式，但這並不便於進行單步操作。我這採用棧方式來實現，將中間結果存下來，以便下一步操作，然後上一步的功能是通過vector陣列，存下已進行的操作。然後主要利用的SetTimer和KillTimer來實現演示，加快及減慢則是通過修改Timer的執行時間間隔。

三、區域性功能實現

1、繪畫背景圖

void CMyDlg::ShowBg(CDC * dc)

void CMyDlg::ShowBg(CDC * dc){

	//顯示背景
	CDC pdc, ddc;
	pdc.CreateCompatibleDC(dc); // 建立一個臨時顯示裝置
	ddc.CreateCompatibleDC(dc); // 建立一個載入盤子的臨時顯示裝置

	CBitmap bmp, * obmp;
	bmp.LoadBitmap(IDB_BG); // 載入背景圖片

	obmp = pdc.SelectObject(&bmp); // 將圖片顯示在裝置pdc上。

	//顯示盤子
	int n[] = {0, 0, 0}; // 用於存放每個柱子已顯示多少盤子
	for(int i = 0; i < number ; i++){
		CBitmap dbmp, * odbmp;
		dbmp.LoadBitmap(IDB_B7 - i); // 載入從大到小第i個盤子圖片
		odbmp = ddc.SelectObject(&dbmp); // 將盤子顯示在裝置ddc上。
		pdc.BitBlt(10 + 150*dish[i], 225 - n[dish[i]]*20, 140, 15, &ddc, 0, 0, SRCCOPY); // 將ddc拷貝到臨時顯示裝置pdc對應位置上
		n[dish[i]] ++;
		ddc.SelectObject(odbmp); // 顯示完畢，還原裝置
	}

	dc->BitBlt(10, 10, 460, 260, &pdc, 0, 0, SRCCOPY); // 將pdc拷貝到程式顯示裝置dc上
	pdc.SelectObject(obmp); // 顯示完畢，還原裝置
}
 

void CMyDlg::OnBnClickedNextButton()

void CMyDlg::OnBnClickedNextButton()
{
	// TODO: 在此新增控制元件通知處理程式程式碼
	flag1 = true;
	if (0 == number) {
		MessageBox("請選擇盤子數！");
		return;
	}
	if (!flag)
	{
		CMyDlg::OnButton1();
	}
	else if (idx < int(res.size() - 1))
	{
		++idx;
		dish[res[idx].num] = res[idx].end;
		Invalidate(FALSE);//重繪
	}
	else
		SetTimer(1015, last, NULL);
}
 

void CMyDlg::OnBnClickedPrevButton()
{
	// TODO: 在此新增控制元件通知處理程式程式碼
	flag1 = true;
	//char str[10];
	//sprintf(str, "%d\n", idx);
	//MessageBox(str);
	if (idx >= 0)
	{
		dish[res[idx].num] = res[idx].beg;
		--idx;
		Invalidate(FALSE);//重繪
	}
}

//加快
void CMyDlg::OnBnClickedButton3()
{
	// TODO: 在此新增控制元件通知處理程式程式碼
	if (last > 100)
	{
		last -= 100;
		UpdateData(FALSE);
		KillTimer(1015);
		SetTimer(1015, last, NULL);
	}
}

//減慢
void CMyDlg::OnBnClickedButton4()
{
	// TODO: 在此新增控制元件通知處理程式程式碼
	CString str;
	
	if (last < 800)
	{
		CString str;
		last += 100;
		UpdateData(FALSE);
		KillTimer(1015);
		SetTimer(1015, last, NULL);
	}
}

四、參考工程

本人程式碼是參考網上修改的，感覺實現上應該還有有待提高的地方，各位可根據需求進行修改，工程環境是VS2015 + MFC。工程已上傳