前言

最近3個月內，無論是現場賽還線上賽中SPLAY出現的概率大的驚人啊啊啊！！！
然而不會的我就GG了，同時發現大家都會SPLAY，，，，然後就學習了一波。

開始怎麼學都學不懂，直到看到一句話

想學好splay,只要把伸展和旋轉操作弄懂,就好了.
(而這兩個想要學會就是需要自己畫圖自己理解了)

於是茅塞頓開,有了本文,
本文重點是SPLAY維護序列的操作,而非SPLAY本身,這部分會說的比較粗略,二叉樹的部分更不會有說明,

菜(sha3)逼我也只是初學,如果有描述不當甚至錯誤的地方,歡迎指正

定義

伸展樹（Splay Tree），也叫分裂樹，是一種二叉排序樹，它能在O(log n)內完成插入、查詢和刪除操作。

同其他平衡樹一樣,都是在二叉排序樹的基礎上進行操作的,但不同於AVL需要記錄平衡資訊,也沒有紅黑樹實現上的難度.是一種綜合考量下很適合應用於資訊學競賽的平衡樹.

對於一個基本的SPLAY 我這樣定義

int ch[N][2];  //ch[][0] 表示左兒子 ch[][1] 表示右兒子
int f[N];      //節點的父親節點
int sz[N];     //當前節點給所在的子樹的節點個數
int val[N];    //當前節點表示的值
int cnt[N];    //當前節點所表示的值的個數
int root;      //記錄根節點的
int tot;       //計算樹中節點個數

構建的過程也就和普通二叉樹一樣了,遞迴下去即可

void newnode(int rt,int v,int fa){
    f[rt]=fa;
    val[rt]=v;sz[rt]=1;
    ch[rt][0]=ch[rt][1]=0;
}
void delnode(int rt){
    f[rt]=sz[rt]=val[rt]=0;
    ch[rt][0]=ch[rt][1]=0;
}
void build(int &rt,int l,int r,int fa){
    if(l>r) return ;
    int m = r+l >> 1;
    rt=m; newnode(rt,val[rt],fa);cnt[rt]=1
 
;
    build(ch[rt][0],l,m-1,rt);
    build(ch[rt][1],m+1,r,rt);
    pushup(rt);
}

void init(int n){
    root=0;
    f[0]=sz[0]=ch[0][0]=ch[0][1]=rev[0]=0;
    build(root,1,n,0);
    pushup(root);
}

旋轉

對於一顆二叉排序樹,根據序列的資訊很容易找到某一個值,只要不斷的向下搜尋下去即可,複雜度是O(樹高),
但是二叉樹最壞的情況下是會退化成一個單鏈的,這是後查詢的複雜度就是O(n)了,非常不可取

而在SPLAY中控制樹保持平衡需要的就是旋轉操作,是樹保持平衡,這樣複雜度就變成了均攤O(logn)的了

單旋: 左旋(zag)&右旋(zig)

雙旋:

通過樹的旋轉來自我調整來保持平衡,就是基於這兩個操作左旋(zag)&右旋(zig),還有其延伸出的操作

下面來實現下旋轉操作

總之就是對每次旋轉節點間關係資訊發生改變的位置調整好就行
需要點耐心,不要調錯

void rotate(int x,int k){   // k = 0 左旋， k = 1 右旋
    int y=f[x];int z=f[y];
    pushdown(y),pushdown(x);
    ch[y][!k]=ch[x][k];if(ch[x][k])f[ch[x][k]]=y;
    f[x]=z;if(z)ch[z][ch[z][1]==y]=x;
    f[y]=x;ch[x][k]=y;
    pushup(y),pushup(x);
}

伸展

經過多次旋轉,將節點位置坐出調整的操作就是伸展了

來舉個栗子，對於一個退化為單鏈的樹進行旋轉

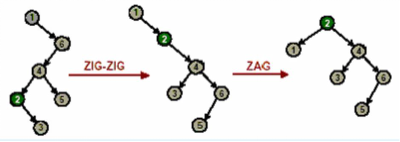
雙旋的寫法，比較穩定

void splay(int x,int goal){//將x旋轉到goal的下面  
    while(f[x] != goal){  
        if(f[f[x]] == goal) rotate(x , ch[f[x]][0] == x);  
        else   {  
            int y=f[x],z=f[y];  
            int K = (ch[z][0]==y);  
            if(ch[y][K] == x) rotate(x,!K),rotate(x,K);  
            else rotate(y,K),rotate(x,K);  
        }  
    }  
    pushup(x);  
    if(goal==0) root=x;  
}  

而我發現zig-zag這種兩個旋轉合在一起的操作,其實是兩遍單旋,所以只要每次都向上單旋就行了,

單旋容易被卡 不懂 百度伸展樹單雙旋的比較
void splay(int x,int goal){  //將x調整為goal的兒子,(如果要調整到根goal就是0)
    for(int y=f[x];f[x]!=goal;y=f[x])
        rotate(x,(ch[y][0]==x)); //(ch[y][0]==x)計算是左旋還是右旋,看x是左右兒子哪一個區分開了
    if(goal==0) root=x;
}

各種操作

對於SPALY能夠做到的操作以【BZOJ3224 普通平衡樹】為引,以 【BZOJ 1895 & POJ 3580 supermemo 】做補充,如果不完全,後期會補上

一些基本操作

查詢

查詢部分和普通的二叉查詢樹一模一樣,只要遍歷下去即可

int search(int rt,int x){
        if(ch[rt][0]&&val[rt]>x) return search(ch[rt][0],x);
    else if(ch[rt][1]&&val[rt]<x)return search(ch[rt][1],x);
    else return rt;
}

極值 & 前驅,後繼

前驅:小於x的最大的數
後繼:大於x的最小的數

先找到x所在的節點,然後在左右子樹,找最右左的節點即可

//以x為根的子樹 的極值點  0 極小 1 極大
int extreme(int x,int k){
    while(ch[x][k])x=ch[x][k];splay(x,0);
    return x;
}

第K個數

第k個數,通過記錄的sz[],很容易得到每個節點是第幾個,不斷的在樹上二分就行,

//以x為根的子樹 第k個數的位置
int kth(int x,int k){
    if(sz[ch[x][0]]+1==k&&k<=sz[ch[x][0]]+cnt[x]) return x;
    else if(sz[ch[x][0]]>=k) return kth(ch[x][0],k);
    else return kth(ch[x][1],k-sz[ch[x][0]]-cnt[x]);
}

一些正經的操作

插入

假如要插入的點已經存在了,那麼cnt++就行了,
假如要插入的點在x
那麼讓x-1做為樹根,x+1伸展到根節點下面,那麼x+1的左兒子就是空出來的 加個值就好了

void _insert(int x){
    int y=search(root,x),k=-1;
    if(val[y]==x){
        cnt[y]++;
        sz[y]++;
        for(int yy=y;yy;yy=f[yy]) pushup(yy);
    }
    else {
        int p=prec(x),s=sufc(x);
        splay(p,0);splay(s,p);
        newnode(++tot,x,ch[root][1]);
        ch[ch[root][1]][0]=tot;
        for(int z=ch[root][1];z;z=f[z])pushup(z);
    }
    if(k==-1) splay(y,0);else splay(tot,0);
}

刪除

和刪除一樣,就是反過來了而已,
首先這個值如果不存在,那就直接return即可
如果這個值大於1,那就cnt–即可
如果這個值所在的節點的兒子節點有空的,那麼就把需要提上去的兒子節點提上去即可
如果這個值所在的節點的兒子節點都存在,那麼就把這個節點的前驅提到根節點,後繼提到根節點的下面,那樣的話刪除ch[ch[root][1]][0]就行了

void _delete(int x){
    int y=search(root,x);
    if(val[y]!=x) return;
    if(cnt[y]>1){
        cnt[y]--;
        sz[y]--;
        for(int yy=y;yy;yy=f[yy]) pushup(yy);
    }
    else if(ch[y][0]==0||ch[y][1]==0){
        int z=f[y];
        ch[z][ch[z][1]==y]=ch[y][ch[y][0]==0];
        f[ch[y][ch[y][0]==0]]=z;delnode(y);
        for(int yy=z;yy;yy=f[yy]) pushup(yy);
    }
    else {
        int p=prec(x),s=sufc(x);
        splay(p,0);splay(s,p);
        ch[ch[root][1]][0]=0;
        delnode(ch[ch[root][1]][0]);
        for(int yy=s;yy;yy=f[yy]) pushup(yy);
    }
}

區間加

區間操作

對於區間[l,r]
那麼讓l-1做為樹根,r+1伸展到根節點下面,那麼r+1的左兒子就是這個區間
打上lazy_tag就行了

但為了更好的處理[1,n]這個區間 加上個0和n+1這兩個節點

//區間加
void add(int l,int r,int v){
    int x=kth(root,l-1),y=kth(root,r+1);
    splay(x,0);splay(y,x);
    update_add(ch[y][0],v);
}

區間翻轉

同樣在一個二叉樹中 翻轉也就是讓每個節點的兩個兒子交換一下順序就好了,, 打個標記 就行了,

//區間翻轉
void reversal(int l,int r){
    int x=kth(root,l-1),y=kth(root,r+1);
    splay(x,0);splay(y,x);
    update_rev(ch[y][0]);
}

區間交換

所以我們可以將後一個區間處理到一個子樹上,然後放到l−1,l 這兩個節點之間,就好了,先減掉,然後在加上去就好了

//區間交換
void exchange(int l1,int r1,int l2,int r2){
    int x=kth(root,l2-1),y=kth(root,r2+1);
    splay(x,0),splay(y,x);
    int tmp_right = ch[y][0]; ch[y][0]=0;
    x=kth(root,l1-1),y=kth(root,l1);
    splay(x,0),splay(y,x);
    ch[y][0] = tmp_right;
    f[tmp_right]=y;
}

合併

合併是指兩顆SPLAY進行合併,
要求這兩顆樹沒有交錯的部分,(可能沒有這個限制,但是我不會,)

首先處理好一個樹A加入到B中,那麼在B中騰出一個空節點來代替A樹需要的段，然後把A樹的樹根放到呢個騰出的空節點位置就行了，

總結

SPLAY操作非常靈活多變,一定要理解SPLAY然後去使用,不要只會套板子就結束了,

有幾點特別要注意的地方
1.插入/刪除節點的時候注意父節點要修改
2.sz[]維護不要出錯
3. ……

——————————————————————————-

附上整體程式碼-md貼上來太卡了,去題解裡看吧
注：這兩個板子沒有用雙旋，用的單旋。。