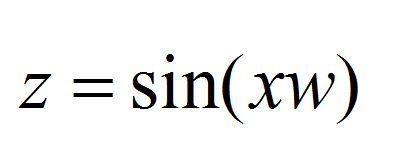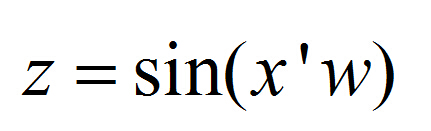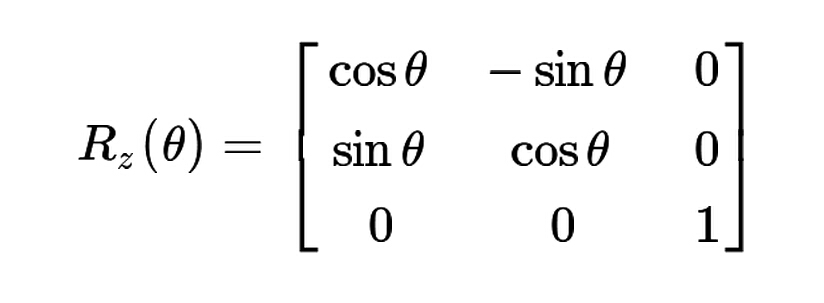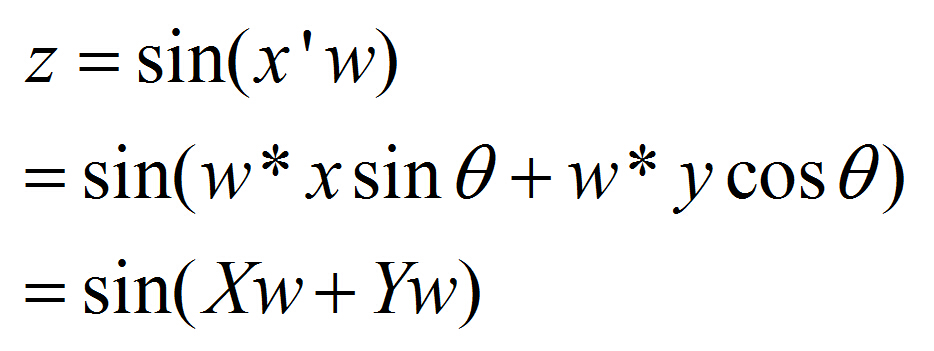OpenCV17(影象二維頻譜的理解,傅立葉頻譜分析)
傅立葉變換的理解參考教程:http://blog.jobbole.com/70549/
這個已經說得很詳細了。
不過這個說明只是針對一維的傅立葉變換,在影象處理中我們最常見的還是二維頻譜,二維頻譜到底該怎麼看呢?以下是我的理解,謝謝某人的幫助。
1.先看一段MATLAB程式碼
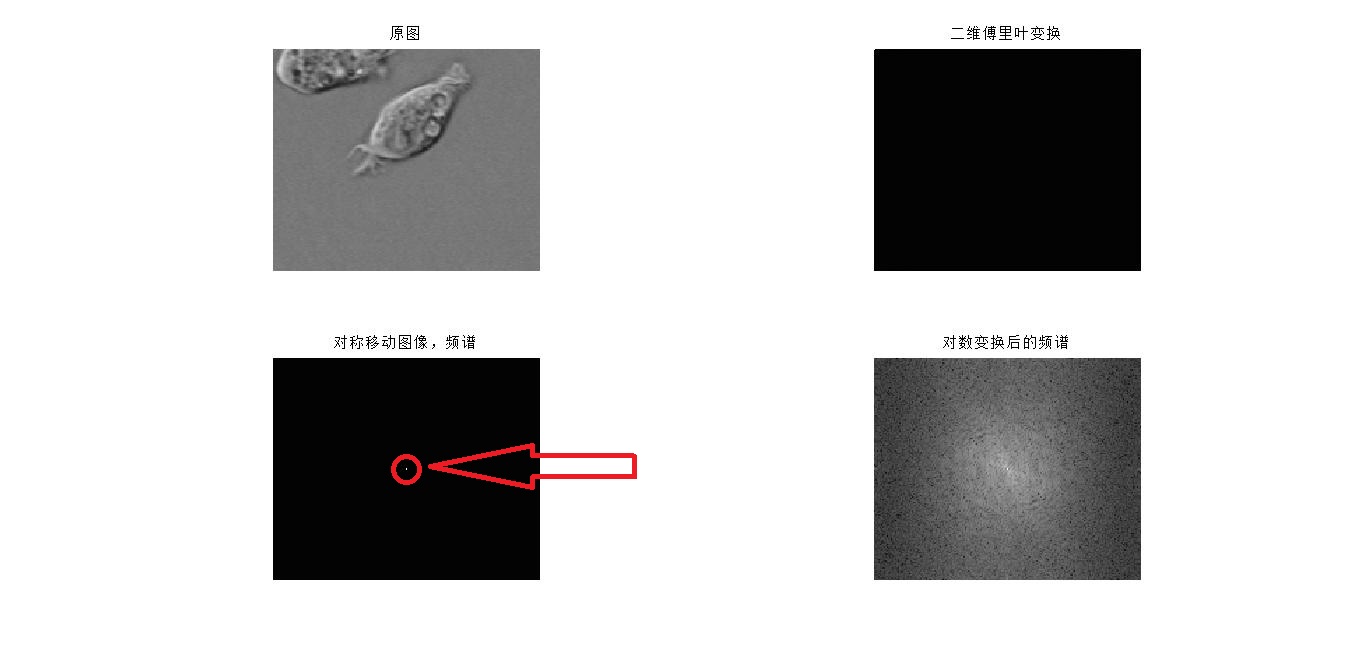
I = imread('cell.tif'); fI = fft2(I); sfI = fftshift(fI); temp = log(1+abs(sfI)); subplot(2,2,1),imshow(I),title('原圖'); subplot(2,2,2),imshow(fI,[]),title('二維傅立葉變換'); subplot(2,2,3),imshow(sfI,[]),title('對稱移動影象,頻譜'); subplot(2,2,4),imshow(temp,[]),title('對數變換後的頻譜');
cell.tif是MATLAB自帶的圖,結果如下:
2.一個概念
我們知道矩形波可以看作是有無數的不同相位和幅值的正弦函式組成,類似的,一個任意的平面波也可以看成是特定的某幾種正弦波的組合。如圖所示
(《數字影象處理與機器視覺:Visual C++與Matlab實現》P183)
(a)圖上的“JC”的亮度不同,將其亮度作為縱座標,於是得到圖(b)。圖(b)可以看作是圖(c)中的某幾個正弦平面波的組合,注意,正弦平面波的相角、幅值、傳播方向都可以是不同的。
3.推導一個結論
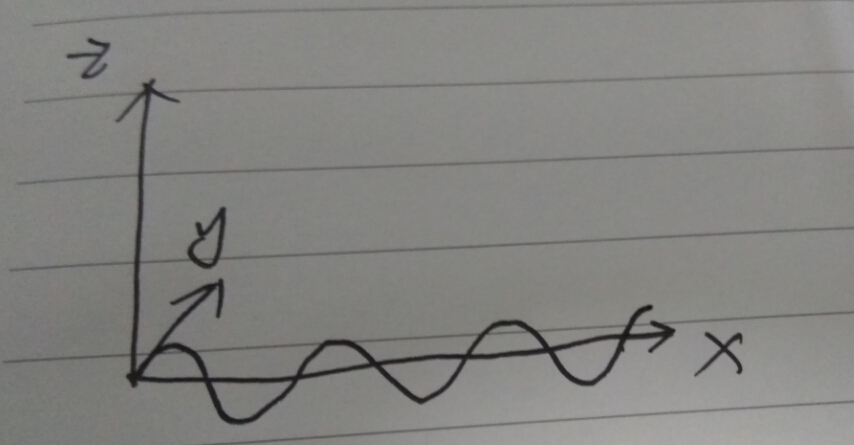
想象有一個正弦平面波(書上原話,有點迷惑人,不是平面,是曲面其實
得正弦平面波的方程為下式,w是相位,設相角為零
從z軸往下看去,得
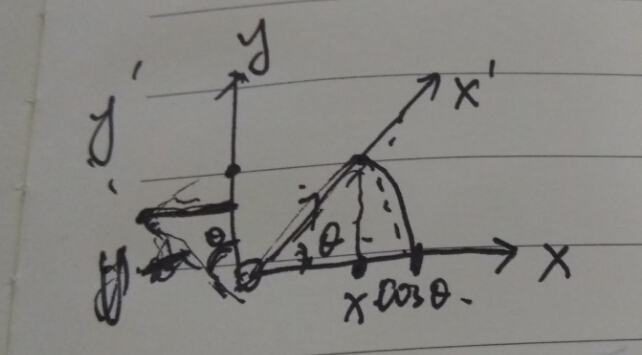
繞z軸旋轉座標系,得新座標系(x',y')
注意,這步是為了推倒 x' 方向上的正弦平面波的方程。可知,這時候的正弦平面波方程為
沿z軸旋轉 theta 角度 的旋轉矩陣是
所以得下式(這步計算不明白沒關係,只要知道這個矩陣可以表示兩個座標的轉化關係即可,會用就行)
所以就等到,旋轉之後的正弦平面波的方程可以表示為
結論!!
其實這一堆只是為找到一般正弦平面波的方程,有什麼用呢?有點用。
4.和頻譜的關係
頻譜的中心為低頻,外圍是高頻成分
可以將頻譜的中心看做座標原點,橫軸為x軸,縱軸是y軸,建立座標系。
頻譜平面上的座標(X,Y)的黑白,表示影象是否含有z = sin(Xw + Yw)這個正弦平面波成分,白即是有含有。
這裡就要再注意一個問題,這裡提到的頻譜是頻譜圖的圖3,再看一下頻譜圖,就是那個有圈圈的
是不是有點亂,所以最後我們來說明這幾張圖都是怎麼來的。
5.頻譜圖的關係
fft2之後,結果是圖2,這是原始的頻譜,但是由於計算中,高頻在中間,低頻在外圍,所以不好看。
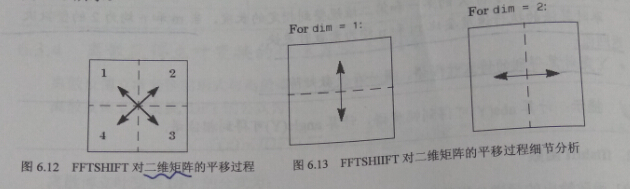
fftshift之後,做了以下對稱變換,將低頻調整到中間,高頻在外圍。注意圖3中心的亮點。這表示原圖中的低頻成分比較多,也就是說影象的灰度變化不大,沒有大的梯度值
由於圖3的對比度不高,看不清楚,所以才出現了最常見到的頻譜,圖4
對數變換log(1+abs(XXX)),這樣就看的清楚些了。
Bingo!
相關推薦
OpenCV17(影象二維頻譜的理解,傅立葉頻譜分析)
傅立葉變換的理解參考教程:http://blog.jobbole.com/70549/ 這個已經說得很詳細了。 不過這個說明只是針對一維的傅立葉變換,在影象處理中我們最常見的還是二維頻譜,二維頻譜到底該怎麼看呢?以下是我的理解,謝謝某人的幫助。 1.先看一段MATLAB
拉普拉斯變換,傅立葉變換;Z變換,離散時間傅立葉變換(DTFT);離散傅立葉變換(DFT)之間的關係及理解
頻域與時域之間的關係是: 時域離散——頻域週期; 時域週期——頻域離散; 對於連續時間訊號 1.拉普拉斯變換: X (
HDU 5126 stars(求四維偏序,cdq分治+樹狀陣列)
Problem Description John loves to see the sky. A day has Q times. Each time John will find a new star in the sky, or he wants to know h
11.頻域裡的卷積——介紹,傅立葉變換和卷積,快速傅立葉變換(FFT)_1
目錄 介紹 FFT 介紹 我們將繼續討論頻率分析以及如何用頻率分量的概念來研究影象。如果你還記得上次我們講過的基於頻率的影象分解的概念。我們通過給你們看這張照片來回憶它(如圖)。這是著名的Dali圖片,當你在那裡允許高頻影象時,你會看到一個女人在欣賞地中海之類的東
負數,傅立葉變換,反傅立葉變換(錯)
#include <QCoreApplication> #include "C:\Users\Administrator\Desktop\fftw\fftw-3.3.4-dll32\fftw3.h" #include "D:\Qt\Eigen\Dense" #include <stdi
數學(論)裡的一些定理(莫比烏斯反演,傅立葉變換,數論變換...)
莫比烏斯反演在數論中佔有重要的地位,許多情況下能大大簡化運算。那麼我們先來認識莫比烏斯反演公式。 定理:和是定義在非負整數集合上的兩個函式,並且滿足條件,那麼我們得到結論 在上面的公式中有一個函式,它的定義如下: (1)若,那麼
理解離散傅立葉變換(一. 傅立葉變換的由來)
理解離散傅立葉變換(一) ------傅立葉變換的由來 關於傅立葉變換,無論是書本還是在網上可以很容易找到關於傅立葉變換的描述,但是大都是些故弄玄虛的文章,太過抽象,盡是一些讓人看了就望而生畏的公式的羅列,讓人很難能夠從感性上得到理解
傅立葉分析和影象的傅立葉頻譜解析
1、為什麼要進行傅立葉變換,其物理意義是什麼? 傅立葉變換是數字訊號處理領域一種很重要的演算法。要知道傅立葉變換演算法的意義,首先要了解傅立葉原理的意義。 傅立葉原理表明:任何連續測量的時序或訊號,都可以表示為不同頻率的正弦波訊號的無限疊加。而根據該原理創立的傅立葉變換演算
如何理解離散傅立葉變換(一)實數形式傅立葉變換
如何理解離散傅立葉變換(一) ——實數形式傅立葉變換 -----------------------------------------------------------------------------------------------------------
《數字影象處理》學習筆記(五)--傅立葉變換
一、一維傅立葉變換及其反變換 單變數離散函式f(x)(其中x=0,1,2,....,M-1)的傅立葉變換F(u)定義為等式: 同樣給出F(u),能用逆DFT來獲得原函式: 從尤拉公式中得到: 得出: 一個恰當的比喻是將傅立葉變換比做一個玻璃稜鏡。稜鏡是可以將光分成不
c語言數字影象處理(六):二維離散傅立葉變換
基礎知識 複數表示 C = R + jI 極座標:C = |C|(cosθ + jsinθ) 尤拉公式:C = |C|ejθ 有關更多的時域與複頻域的知識可以學習複變函式與積分變換,本篇文章只給出DFT公式,性質,以及實現方法 二維離散傅立葉變換(DFT) 其中f(x,y)為原影象,F(u,
陣列(隨機生成一維陣列),二維陣列的概念和題目設計(利用二維陣列 :任意給定分數去計算科目和人均平均分)
1 //陣列間的關係arr[]中的數字為幾,[]內就有幾個數 2 //{ }內的數是從0開始,如需要列印應從0開數 3 如{2,6,9,8,7}列印arr[4]就是7 4 #include <stdio.h> 5 #include <stdlib.h> 6 int
Android超方便 整合 Zxing實現掃一掃,閃光燈,生成二維碼圖片,解析二維碼(條碼)等功能
之前我寫過一篇部落格是關於如何將zxing整合到Android Studio中,以及簡單的實現掃一掃功能。 詳情請看:Android Studio整合Zxing掃一掃 但是,上面那篇部落格只有有一個掃一掃功能,而且在低解析度手機上會出現變形的問題。掃描速度也
數字影象處理筆記——二維離散傅立葉變換(2D Discrete Fourier Transform)
二維傅立葉變換 我們先來看看一維情況的傅立葉變換。在訊號系統中講過連續時間的傅立葉變換和離散時間的傅立葉變換,連續時間傅立葉變換在頻譜上時非週期的,離散時間傅立葉變換(DTFT)在頻譜上是週期的。在DSP中講了離散傅立葉變換,它的思想是將時域週期化,反映在頻域上就是對連續的週期頻譜進行抽樣
Unity3d 二維碼功能(掃碼及相簿讀取,適配ios與android)
EasyCodeScanner外掛包含了掃碼及圖片識別功能。但是隻有ios部分的。android部分使用zbar的開源包實現的EasyCodeScanner匯入Xcode報錯解決方案開啟BuildPh
二維陣列、影象的傅立葉變換(附加反變換與濾波演算法)
FFT演算法原理就不解釋了,可以搜尋一下百度即可。 在二維變換中,需要對矩陣進行一行一行,一列一列的FFT變換,具體公式為: F(u,v)=sum(i=0->M-1)sum(j=0->N-1)f(i, j) * exp(-j2πui/M-j*2π
影象傅立葉變換(二維離散傅立葉變換)
影象傅立葉變換 二維離散傅立葉變換是將影象從空間域轉至頻域,在影象增強、影象去噪、影象邊緣檢測、影象特徵提取、影象壓縮等等應用中都起著極其重要的作用。理論基礎是任意函式都可以表示成正弦函式的線性組合的形式。公式如下 逆變換公式如下 令 R(u,v) 和 I(u,c) 分別表示 F
掃描影象二維碼摳圖(傾斜校正 去黑邊)
標籤:des 演算法 class style log com http it si 由於要識別掃描器得到的圖片,直接將得到的圖片進行識別,並不能得到識別結果,筆者使用的是zbar類,只能正常識別只含有二維碼影象的圖片。於是將二維碼從圖中扣出來就成了工作中的一個需求。(網上有
在OpenCV環境下寫的灰度影象二維傅立葉換,幅值計算,頻譜平移和將數值歸一化到0到255區間的四個函式
影象處理開發資料、影象處理開發需求、影象處理接私活掙零花錢,可以搜尋公眾號"qxsf321",並關注! 影象處理開發資料、影象處理開發需求、影象處理接私活掙零花錢,可以搜尋公眾號"qxsf321",並關注! 影象處理開發資料、影象處理開發需求、影象處理接私活掙零花錢,可以搜尋
數字影象處理之二維影象的傅立葉變換(1)
1.1、訊號變化越快,說明頻率越大,訊號變化越慢,說明頻率越小。這裡的頻率不一定是通常意義上的頻率,通常的頻率是指週期的倒數,我們把通常意義上的頻率叫時間頻率。廣義上的頻率是指變化的快慢,比如圖片來說,從這個畫素到另外一個畫素的灰度值差距比較大,那麼頻率就比較高