本文主要使用markdown進行編輯的。

概述

在講述梯度下降演算法之前，我們先需要了解一下導數（derivative）、偏導數（partial derivative）和方向導數（directional derivative），然後我們看看梯度下降法（Gradient Descent），瞭解為什麼在優化問題中使用梯度下降法來優化目標函式。

導數

一張關於導數和微分的圖：

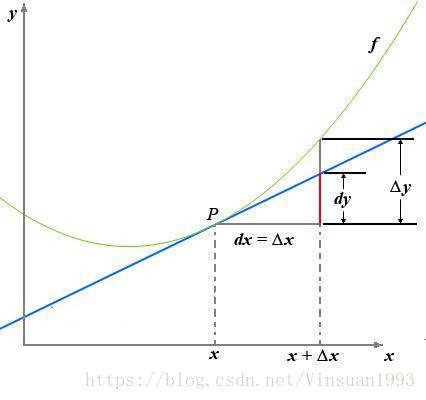
導數定義如下：

反映的是函式y=f(x)在某一點處沿x軸正方向的變化率。再強調一遍，是函式f(x)在x軸上某一點處沿著x軸正方向的變化率/變化趨勢。直觀地看，也就是在x軸上某一點處，如果f’(x)>0，說明f(x)的函式值在x點沿x軸正方向是趨於增加的；如果f’(x)<0，說明f(x)的函式值在x點沿x軸正方向是趨於減少的。

　這裡補充上圖中的Δy、dy等符號的意義及關係如下：
　Δx：x的變化量；
　dx：x的變化量Δx趨於0時，則記作微元dx；
　Δy：Δy=f(x0+Δx)-f(x0)，是函式的增量；
　dy：dy=f’(x0)dx，是切線的增量；
　當Δx→0時，dy與Δy都是無窮小，dy是Δy的主部，即Δy=dy+o(Δx).

導數與偏導數

偏導數的定義如下：

可以看到，導數與偏導數本質是一致的，都是當自變數的變化量趨於0時，函式值的變化量與自變數變化量比值的極限。直觀地說，偏導數也就是函式在某一點上沿座標軸正方向的的變化率。
　區別在於：
　導數，指的是一元函式中，函式y=f(x)在某一點處沿x軸正方向的變化率；
　偏導數，指的是多元函式中，函式y=f(x1,x2,...,xn)$y=f(x_1,x_2,...,x_n)$在某一點處沿某一座標軸(x1,x2,...,xn)$(x_1,x_2,...,x_n)$正方向的變化率。

導數與方向導數

方向導數的定義如下：