deep learning PCA(主成分分析)、主份重構、特徵降維
前言
前面幾節講到了深度學習採用的資料庫大小為28×28的手寫字,這對於機器學習領域算是比較低維的資料,一般圖片是遠遠大於這個尺寸的,比如256×256的圖片。然而特徵向量的維數過高會增加計算的複雜度,像前面訓練60000個28×28的手寫字,在我這個4G記憶體,CORE i5的CPU上訓練需要3個小時,如果你使用GPU當然會增加訓練的速度。維數過高會對後續的分類問題帶來負擔,實際上維數過高的特徵向量對於分類效能(識別率)也會造成負面的影響。很多人認為提取的特徵維數越高對提高識別有用,然而事實並不是我們通常想的,因為一張圖片中的很多特徵是相關的。也就是選取合適的特徵向量對提高識別率有很大的影響。因此就出現了
快速PCA演算法
PCA的計算中最主要的工作是計算樣本的協方差矩陣的特徵值和特徵向量,當然這對於MATLAB來說是非常容易的了。設樣本矩陣X的大小為n×d,n代表樣本的個數,d代表一個樣本的特徵向量。則樣本的散佈矩陣(協方差矩陣)S是一個d×d的方陣,當維數d較大時,如維數d=10000,那麼S是一個10000×10000的矩陣,這樣非常消耗記憶體,結果就是你的膝上型電腦卡死,CPU使用率變高,記憶體被佔的滿滿的,你無法做任何其他事。這時就出現了快速PCA演算法。
計算散佈矩陣的特徵值和特徵向量,設Z為n×d的樣本舉證X中的每一個樣本減去樣本均值m後得到的矩陣,即散佈矩陣S為Z'Z
設n維列向量v是R的特徵向量,則有
(ZZ')v=λv (1)
將式(1)的兩邊同時左乘Z',並利用矩陣乘法結合律得
(Z'Z)(Z'v)=λ(Z'v) (2)
式(2)說明Z'v為散佈矩陣S=Z'Z的特徵值。這說明可以計算小矩陣R=ZZ'的特徵向量v,而後通過左乘Z'得到散佈矩陣S=Z'Z的特徵向量Z'v。
下面以劍橋大學的ORL人臉庫進行試驗。下面是資料庫中的樣本例子:
STEP 1
生成樣本矩陣,大小為n×d,n代表樣本個數,d代表一個樣本的特徵數。下面是程式碼。
ReadFaces.m
<span style="font-family:Times New Roman;"><span style="font-size:14px;">function [imgRow,imgCol,FaceContainer,faceLabel]=ReadFaces(nFacesPerPerson,nPerson,bTest)
if nargin==0
nFacesPerPerson=5;
nPerson=40;
bTest=0;
elseif nargin<3
bTest=0;
end
img=imread('D:\機器學習\att_faces\s1\1.pgm');
[imgRow,imgCol]=size(img);
FaceContainer=zeros(nFacesPerPerson*nPerson,imgRow*imgCol);
faceLabel=zeros(nFacesPerPerson*nPerson,1);
for i=1:nPerson
i1=mod(i,10);
i0=char(i/10);
strPath='D:\機器學習\att_faces\s';
if(i0~=0)
strPath=strcat(strPath,'0'+i0);
end
strPath=strcat(strPath,'0'+i1);
strPath=strcat(strPath,'/');
tempStrPath=strPath;
for j=1:nFacesPerPerson
strPath=tempStrPath;
if bTest==0
strPath=strcat(strPath,'0'+j);
else
strPath=strcat(strPath,num2str(5+j));
end
strPath=strcat(strPath,'.pgm');
img=imread(strPath);
FaceContainer((i-1)*nFacesPerPerson+j,:)=img(:)';
faceLabel((i-1)*nFacesPerPerson+j)=i;
end
end
save('FaceMat.mat','FaceContainer')</span></span>利用生成的樣本矩陣求特徵值和特徵向量。(1)先求出樣本矩陣特徵的平均值;(2)計算協方差矩陣;(3)計算協方差矩陣前k個特徵值和特徵向量;(4)得到協方差矩陣的特徵向量然後再歸一化;(5)線性變化投影到k維。
fastPCA.m
<span style="font-family:Times New Roman;"><span style="font-size:14px;">function [pcaA V]=fastPCA(A,k)
% A-代表樣本矩陣
% k-代表降至k維
% PcaA-降維後的k維樣本特徵向量組成的矩陣,每一行代表一個樣本,
% 列數k為降維後的樣本矩陣的維數
% V-主成份向量
A=load('FaceMat.mat');
[r c]=size(A);
meanVec=mean(A);%求樣本的均值
Z=(A-repmat(meanVec,r,1));
covMatT=Z*Z'; %計算協方差矩陣,此處是小樣本矩陣
[V D]=eigs(covMatT,k);%計算前k個特徵值和特徵向量
V=Z'*V;%得到協方差矩陣covMatT'的特徵向量
%特徵向量歸一化單位特徵向量
for i=1:k
V(:,i)=V(:,i)/norm(V(:,i));
end
pcaA=Z*V;%線性變化降維至k維
save('PCA.mat','V','meanVec');</span></span>通過前兩步就提取到了樣本的特徵向量和特徵值並存儲在pcaA中。
下面將介紹視覺化主成份臉。V中每一列儲存的是主份特徵,第一列就表示儲存的第一主成份,第二列表示儲存的第二主成份,以此類推。
visualize_pc.m
<span style="font-family:Times New Roman;"><span style="font-size:14px;">function visualize_pc(E)
[size1 size2]=size(E);
global imgRow;
global imgCol;
row=imgRow;
col=imgCol;
figure
img=zeros(row,col);
for ii=1:20
img(:)=E(:,ii);
subplot(4,5,ii);
imshow(img,[]);
end</span></span>main1.m
<span style="font-family:Times New Roman;font-size:14px;">function main1(k)
%k代表降至k維
global imgRow;
global imgCol;
nPerson=40;
nFacesPerPerson=5;
display('讀入人臉資料.....');
[imgRow,imgCol,FaceContainer,faceLabel]=ReadFaces(nFacesPerPerson,nPerson);
display('..................');
nFaces=size(FaceContainer,1);
display('PCA降維.....');
[LowDimFaces W]=fastPCA(FaceContainer,k);
visualize_pc(W);
save('LowDimFaces.mat','LowDimFaces');
display('結束.....');</span> 主份臉重構
對於一張圖片,可以用如下的式子表示:
主份臉重構
對於一張圖片,可以用如下的式子表示:
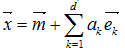
其中e_k分別是散佈矩陣S前k個特徵值對應的特徵向量。a_1,a_2,...,a_k被稱為主成份,可以如下公式表示:
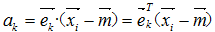
那麼現在可以得到主份臉重構後的影象。結果如下

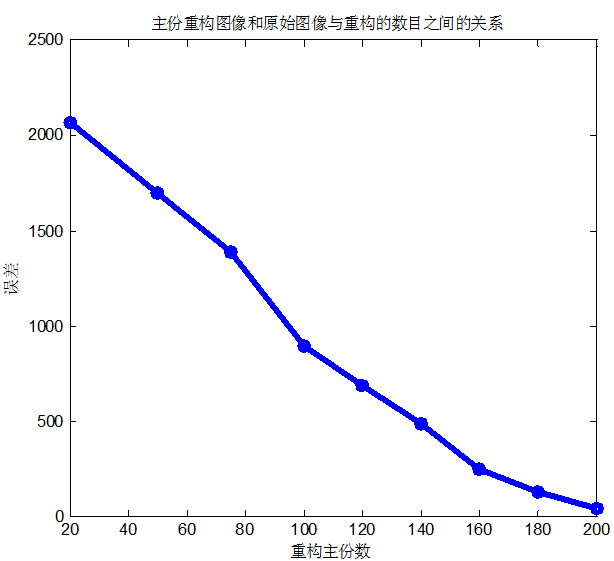
============================================================================================== 第六節:convolution and pooling ==============================================================================================

懷柔風光

