臨時抱佛腳的Machine Learning 01-PCA主成分分析
PCA演算法
作者:桂。
時間:2017-02-26 19:54:26
前言
本文為模式識別系列第一篇,主要介紹主成分分析演算法(Principal Component Analysis,PCA)的理論,並附上相關程式碼。全文主要分六個部分展開:
1)簡單示例。通過簡單的例子,引出PCA演算法;
2)理論推導。主要介紹PCA演算法的理論推導以及對應的數學含義;
3)演算法步驟。主要介紹PCA演算法的演算法流程;
4)應用例項。針對PCA的實際應用,列出兩個應用例項;
5)常見問題補充。對於資料預處理過程中常遇到的問題進行補充;
6)擴充套件閱讀。簡要介紹PCA的不足,並給出K-L變換、Kernel-PCA(KPCA)的相關連結。
本文為個人總結,內容多有不當之處,麻煩各位批評指正。
一、簡單示例
A-示例1:降維
先來看一組學生的成績
| 學生1 | 學生2 | 學生3 | 學生4 | ... | 學生N | |
| 語文成績 | 85 | 85 | 85 | 85 | ... | 85 |
| 數學成績 | 96 | 93 | 78 | 64 | ... | 97 |
為了方便分析,我們假設N=5;
| 學生1 | 學生2 | 學生3 | 學生4 | 學生5 | |
| 語文成績 | 85 | 85 | 85 | 85 | 85 |
| 數學成績 | 96 | 93 | 78 | 64 | 97 |
問題:現在要求大家將成績與不同學生進行匹配。
按【學生,語文成績,數學成績】進行匹配,即:【學生1,85,96】...【學生5,85,97】,可以看到,對於成績【85,97】,我們很容易匹配出學生5;但仔細觀察,他們的語文成績都是相同的,即僅僅用數學成績就可以表達出不同學生,即將資料從二維投影至一維
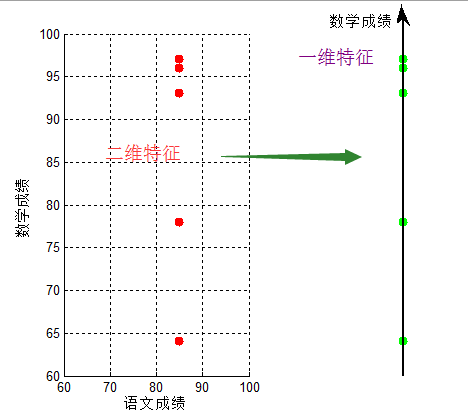
將【語文成績,數學成績】壓縮成只用【數學成績】,實現了資料降維,我們將【語文成績,數學成績】的二維特徵,壓縮成【數學成績】的一維特徵,這就是降維。
B-主成分分析
細心的同學,從上一個圖中可以發現:將資料沿方差最大方向投影,資料更易於區分
在進行理論推導以前,再看一個例子,還是之前5個同學的成績,只不過這次測試他們語文成績也不再相同:
| 學生1 | 學生2 | 學生3 | 學生4 | 學生5 | |
| 語文成績 | 50 | 60 | 70 | 80 | 90 |
| 數學成績 | 80 | 82 | 84 | 86 | 88 |
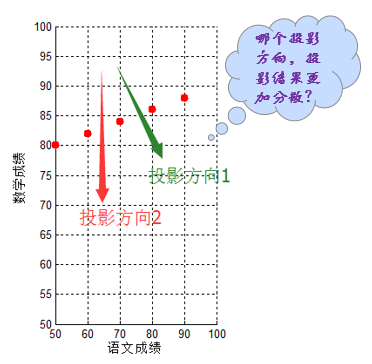
此時如果將二維特徵【語文成績,數學成績】壓縮成1維,僅僅用數學成績表達似乎不是最佳方案,即使沿著投影方向2,只用語文成績表達,其分散程度似乎也比不上投影方向1的降維結果。
如何找到最佳的(方差最大,即最分散。這也容易理解,畢竟分散的資料更容易區分開來)降維方式呢?顯然最佳方案不總是用語文/數學成績單一替代,這便需要本文的主角——PCA演算法。簡而言之:PCA演算法其表現形式是降維,同時也是一種特徵融合演算法。
二、理論推導
進行正式的理論推導之前,先交代幾個常用操作的幾何意義。
A-內積與投影
下面先來看一個高中就學過的向量運算:內積。兩個維數相同的向量的內積被定義為:
(a1,a2,⋯,an)T⋅(b1,b2,⋯,bn)T=a1b1+a2b2+⋯+anbn(a1,a2,⋯,an)T⋅(b1,b2,⋯,bn)T=a1b1+a2b2+⋯+anbn
內積運算將兩個向量對映為一個實數。其計算方式非常容易理解,但是其意義並不明顯。下面我們分析內積的幾何意義。假設A和B是兩個n維向量,我們知道n維向量可以等價表示為n維空間中的一條從原點發射的有向線段,為了簡單起見我們假設A和B均為二維向量,則A=(x1,y1),B=(x2,y2)A=(x1,y1),B=(x2,y2)。則在二維平面上A和B可以用兩條發自原點的有向線段表示,見下圖:
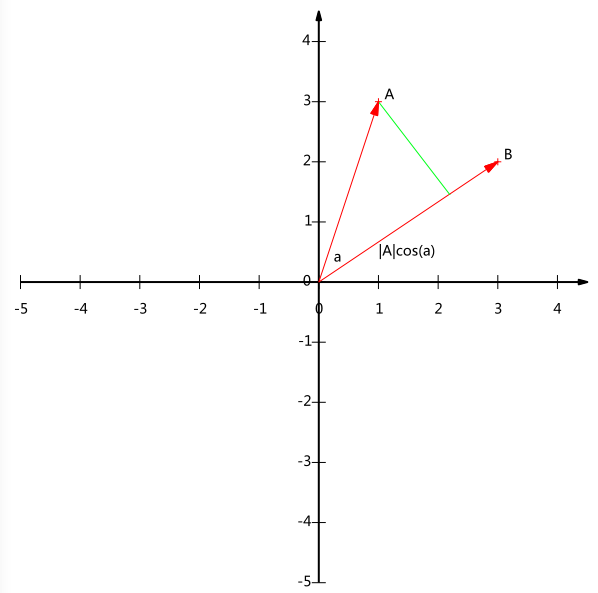
現在我們從A點向B所在直線引一條垂線。我們知道垂線與B的交點叫做A在B上的投影,再設A與B的夾角是a,則投影的向量長度為|A|cos(a)|A|cos(a),其中|A|=x21+y21−−−−−−√|A|=x12+y12是向量A的模,也就是A線段的標量長度。
注意這裡我們專門區分了向量長度和標量長度,標量長度總是大於等於0,值就是線段的長度;而向量長度可能為負,其絕對值是線段長度,而符號取決於其方向與標準方向相同或相反。
到這裡還是看不出內積和這東西有什麼關係,不過如果我們將內積表示為另一種我們熟悉的形式:
A⋅B=|A||B|cos(a)A⋅B=|A||B|cos(a)
現在事情似乎是有點眉目了:A與B的內積等於A到B的投影長度乘以B的模。再進一步,如果我們假設B的模為1,即讓|B|=1|B|=1,那麼就變成了:
A⋅B=|A|cos(a)A⋅B=|A|cos(a)
也就是說,設向量B的模為1,則A與B的內積值等於A向B所在直線投影的向量長度!這就是內積的一種幾何解釋,也是我們得到的第一個重要結論。在後面的推導中,將反覆使用這個結論。
B-基的概念
給出下面這個向量:
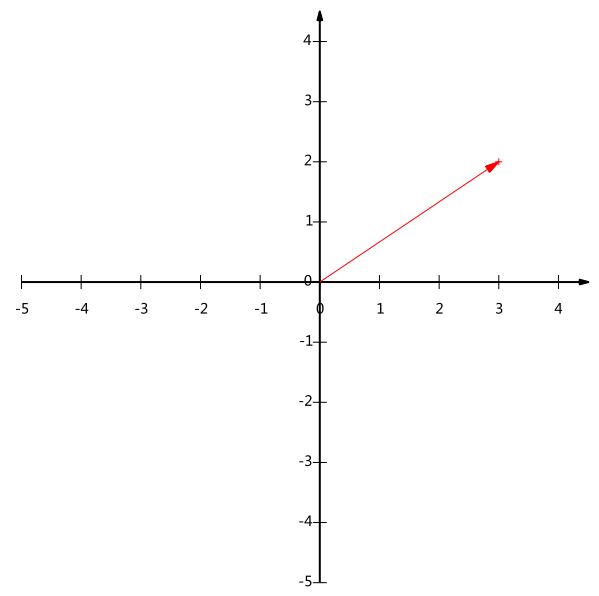
在代數表示方面,我們經常用線段終點的點座標表示向量,例如上面的向量可以表示為(3,2),這是我們再熟悉不過的向量表示。
不過我們常常忽略,只有一個(3,2)本身是不能夠精確表示一個向量的。我們仔細看一下,這裡的3實際表示的是向量在x軸上的投影值是3,在y軸上的投影值是2。也就是說我們其實隱式引入了一個定義:以x軸和y軸上正方向長度為1的向量為標準。那麼一個向量(3,2)實際是說在x軸投影為3而y軸的投影為2。注意投影是一個向量,所以可以為負。
更正式的說,向量(x,y)實際上表示線性組合:
x(1,0)T+y(0,1)Tx(1,0)T+y(0,1)T
不難證明所有二維向量都可以表示為這樣的線性組合。此處(1,0)和(0,1)叫做二維空間中的一組基。
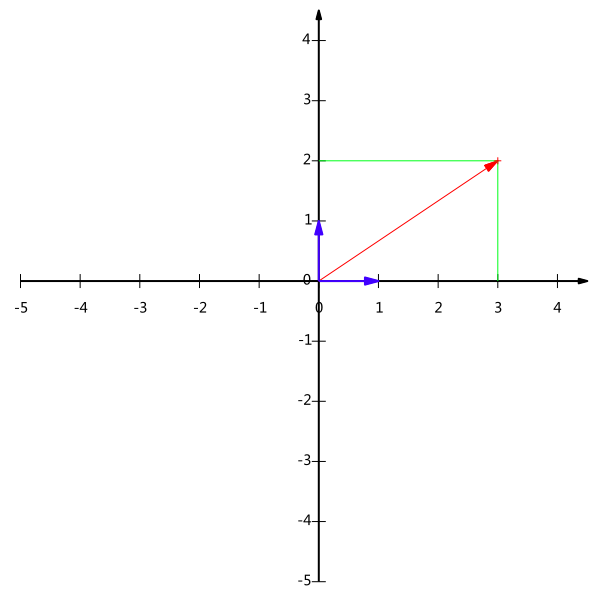
所以,要準確描述向量,首先要確定一組基,然後給出在基所在的各個直線上的投影值,就可以了。只不過我們經常省略第一步,而預設以(1,0)和(0,1)為基。
基就是骨架,基的個數即為撐起給定維度空間的最小向量個數,通常設定基德模為1。
C-基變換的矩陣表示
但基不是唯一的,例如上一個例子中選(1,0)和(0,1)為基,同樣,上面的基可以變為(12√,12√)(12,12)和(−12√,12√)(−12,12)。
現在我們想獲得(3,2)在新基上的座標,即在兩個方向上的投影向量值,就需要利用到基變換的矩陣表示。
根據下圖,我們只要分別計算(3,2)和兩個基的內積,不難得到新的座標為(52√,−12√)(52,−12)
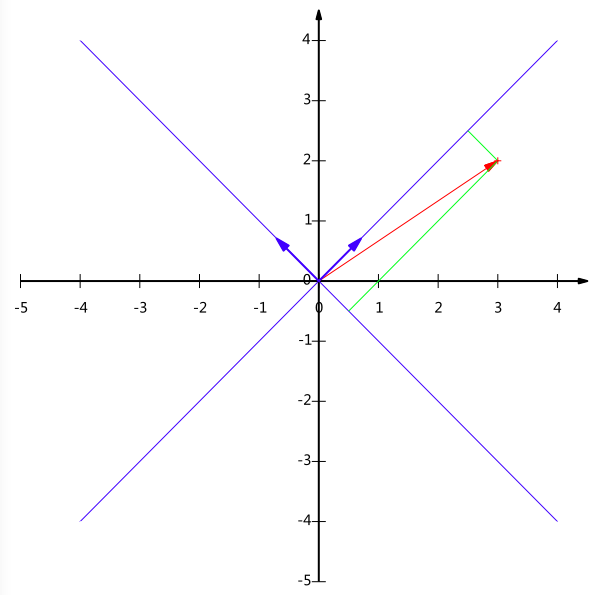
同樣我們可以利用基變換的矩陣表示進行求解:
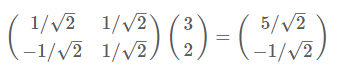
再舉一例:(1,1),(2,2),(3,3),想變換到剛才那組基上,則可以這樣表示:
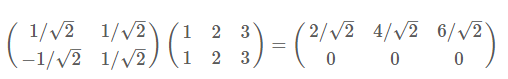 於是一組向量的基變換被幹淨的表示為矩陣的相乘。
於是一組向量的基變換被幹淨的表示為矩陣的相乘。
推廣成一般性結論:
一般的,如果我們有M個N維向量,想將其變換為由R個N維向量表示的新空間中,那麼首先將R個基按行組成矩陣A,然後將向量按列組成矩陣B,那麼兩矩陣的乘積AB就是變換結果,其中AB的第m列為A中第m列變換後的結果。
對應數學表達:
 其中pipi是一個行向量,表示第i個基,ajaj是一個列向量,表示第j個原始資料記錄。
其中pipi是一個行向量,表示第i個基,ajaj是一個列向量,表示第j個原始資料記錄。
上述分析同時給矩陣相乘找到了一種物理解釋:兩個矩陣相乘的意義是將右邊矩陣中的每一列列向量變換到左邊矩陣中每一行行向量為基所表示的空間中去。這種操作便是降維。 D-最優基的選取方法
根據上面的分析,可以得出:只要找出合適的p1,p2,...,pRp1,p2,...,pR,就可以實現對特徵矩陣的投影,從而實現降維。為了便於分析,我們假設此處資料均已做中心化處理(去均值)。
對於未知的投影向量,我們假設投影變換表示為:
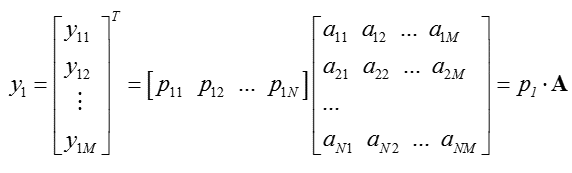
我們希望結果方差最大,即:
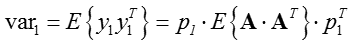
又對於投影向量,有p1pT1=1p1p1T=1,從而方差最大化可轉化為含有拉格朗日乘子的函式:

為了簡化書寫,記:
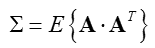
求導並另導數為零,得出最優解:
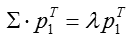
將上式代入方差表示式,得到:
var1=λvar1=λ
若要方差最大,只要特徵值最大即可。由此可以觀察:向量p1p1即為ΣΣ最大特徵值所對應的特徵向量。
同理,p2p2為次大特徵值對應的特徵向量,依次類推,即可求得投影矩陣。
實際操作中,通常藉助特徵值分解(eig)或者奇異值分解(SVD)進行投影空間的構造。
(此處為補充內容,可跳過,不影響整體理解)換一種角度,通過奇異值分解的特性,也可以實現投影向量的理論推導:
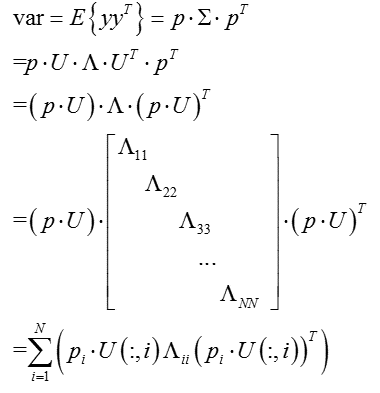
而矩陣的能量為矩陣的跡:

從而方差的大小即為特徵值的大小,從而根據特徵值依次對應的特徵向量,構造投影空間。
E-特徵壓縮
根據上面的推導,得到:
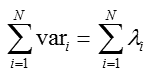
從而可以根據給定比例(如0.9)選定投影空間維度K(方式不唯一,此處僅僅給出參考)

假設投影矩陣為P,從而投影后的資料為:
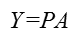
三、演算法步驟
- 步驟一:資料中心化——去均值,根據需要,有的需要歸一化——Normalized;
- 步驟二:求解協方差矩陣;
- 步驟三:利用特徵值分解/奇異值分解 求解特徵值以及特徵向量;
- 步驟四:利用特徵向量構造投影矩陣;
- 步驟五:利用投影矩陣,得出降維的資料。
對應第一部分B-主成分分析 小節的成績,結合演算法步驟,給出MATLAB程式碼:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
|
對應結果圖,可以看出投影變換後新座標軸的方向,即此時投影的間距最大,與上文分析一致:
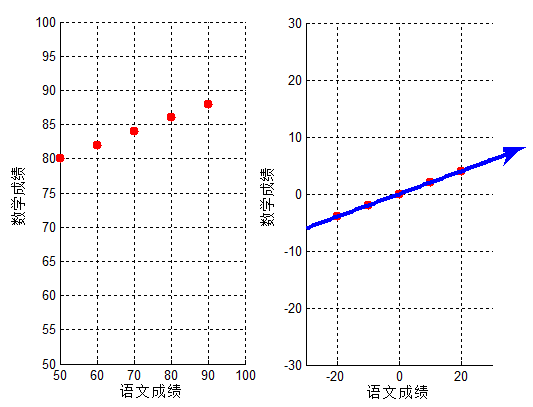
對應完整的程式碼:
四、應用例項
A-示例1:二維資料降維
以

為例,我們用PCA方法將這組二維資料其降到一維。
因為這個矩陣的每行已經是零均值,這裡我們直接求協方差矩陣:
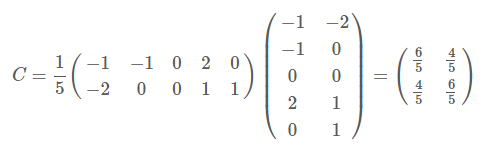
然後求其特徵值和特徵向量,具體求解方法不再詳述,可以參考相關資料。求解後特徵值為:
λ1=2,λ2=2/5λ1=2,λ2=2/5
那麼標準化後的特徵向量為:
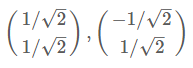
從而得到特徵矩陣P:
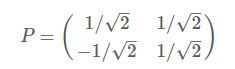
最後我們用P的第一行乘以資料矩陣,就得到了降維後的表示:
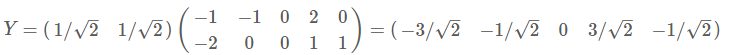
降維投影結果如下圖:

B-示例2:特徵臉提取

為了小白可以理解,此處給一個簡化版的MATLAB程式碼:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
C-示例3:葡萄酒案例
具體可參考:最後給出的連結,不再具體展開。

五、常見問題補充
(如果不配合準則函式-優化問題 ,PCA降維可不必對資料歸一化,只做去均值處理即可。 這句話基本上是廢話...)
- 資料特徵的歸一化,是對整個矩陣還是每一維特徵?
整體做歸一化相當於各向同性的縮放,這樣處理起來沒有作用; 各維分別作歸一化會丟失各維方差這一資訊,但各維之間的相關係數可以保留; 如果本來各維德量綱是相同的,最好不要做歸一化,以儘可能多地保留資訊; 如果本來各維的量綱是不同的,那麼直接做PCA沒有意義,就需要先對各維分別歸一化。
- 為什麼feature scaling 會使gradient descent 的收斂更好?
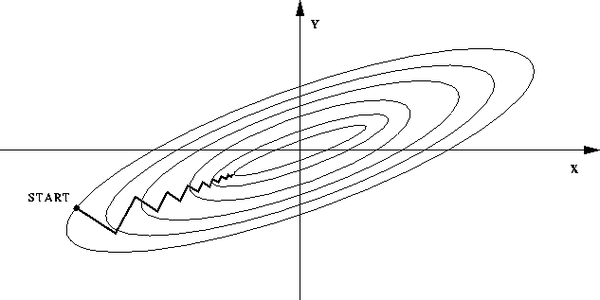
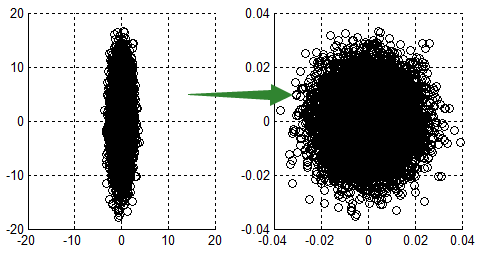
如果不歸一化,各維度特徵的跨度差距很大,目標函式就會是”扁“的:
(圖中橢圓表示目標函式的等高線,兩個座標軸代表兩個特徵) 這樣,在進行梯度下降的時候,梯度的方向就會偏離最小值的方向,走很多彎路。 如果歸一化,那麼目標函式就"圓 "了,從這裡也可以明白:資料歸一化,是針對每一個維度(特徵)而言的,而不是整體。
看,每一步梯度的方向都基本指向最小值,可以大步前進。
以二維特徵為例:
scaling避免了某個特徵過大/小的問題。
- 常見特徵(資料)歸一化的方法?
- 最值歸一化:比如把最大值歸一化成1,最小值歸一化成-1;或把最大值歸一化成1,最小值歸一化成0。適用於本來就分佈在有限範圍內的資料。
六、其他
- Karhunen-Loeve變換(KL變換):PCA為無監督型別,K-L變換則對有監督/無監督的場景都使用,且二者在原理上非常相似,如果有空閒,擬在後續文章進行講解,此處不再展開;
- Kernel-PCA:核PCA (KPCA):PCA從方差角度進行論述,構造協方差矩陣,考慮的是線性關係,對於非線性關係沒有進行討論,Kernel可以將資料對映到高維。具體原理及應用本文不再詳細整理。
參考: