前言

以下內容是個人學習之後的感悟，轉載請註明出處~

簡介

　　在用統計分析方法研究多變量的課題時，變量個數太多就會增加課題的復雜性。人們自然希望變量個數較少而得到的

信息較多。在很多情形，變量之間是有一定的相關關系的，當兩個變量之間有一定相關關系時，可以解釋為這兩個變量反

映此課題的信息有一定的重疊。主成分分析是對於原先提出的所有變量，將重復的變量(關系緊密的變量)刪去多余，建立

盡可能少的新變量，使得這些新變量是兩兩不相關的，而且這些新變量在反映課題的信息方面盡可能保持原有的信息。

　　降維算法有很多，比如PCA、ICA、SOM、MDS、ISOMAP、LLE等，在此不一一列舉。PCA是一種無監督降維算法，

它是最常用的降維算法之一，可以很好地解決因變量太多而復雜性、計算量增大的弊端。

PCA主成分分析原理

1、協方差原理

　　樣本X和樣本Y的協方差(Covariance)：

　　協方差為正時說明X和Y是正相關關系，協方差為負時X和Y是負相關關系，協方差為0時X和Y相互獨立。Cov(X,X)就是

X的方差(Variance).當樣本是n維數據時，它們的協方差實際上是協方差矩陣（對稱方陣），方陣的邊長是C_n²。比如對於3

維數據(x,y,z)，計算它的協方差就是：

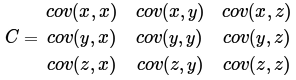
2、SVD分解原理

　　若AX=λX，則稱λ是A的特征值，X是對應的特征向量。實際上可以這樣理解：矩陣A作用在它的特征向量X上，僅僅使得

X的長度發生了變化，縮放比例就是相應的特征值λ。當A是n階可逆矩陣時，A與P^-1Ap相似，相似矩陣具有相同的特征值。

　　特別地，當A是對稱矩陣時，A的奇異值等於A的特征值，存在正交矩陣Q（Q^-1=Q^T），使得：

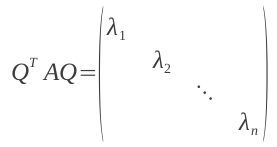
　　對A進行奇異值分解就能求出所有特征值和Q矩陣。A?Q=Q?D,D是由特征值組成的對角矩陣由特征值和特征向量的定

義知，Q的列向量就是A的特征向量。

3、PCA原理及實現

　　PCA主要通過把數據從高維映射到低維來降低特征維度。如下圖所示，但映射的時候要保留盡量多的主要信息。

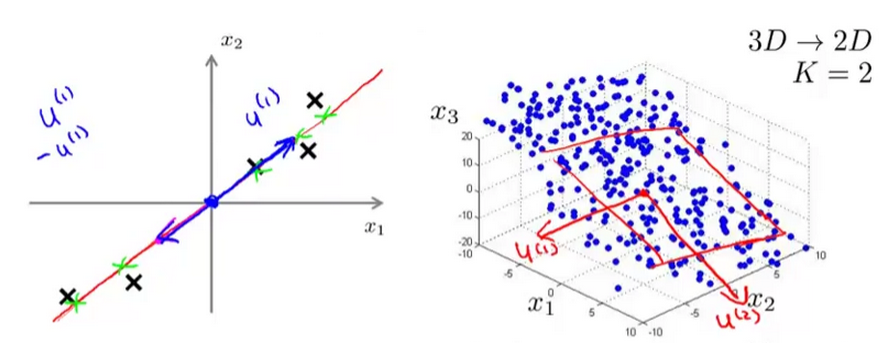
　　PCA的算法步驟如下：

• 輸入數據集x={x⁽¹⁾，x⁽²⁾，x⁽³⁾，.....，x^(m)}、需要降到K維；
• 對所有樣本進行均值歸一化，如右圖所示；　
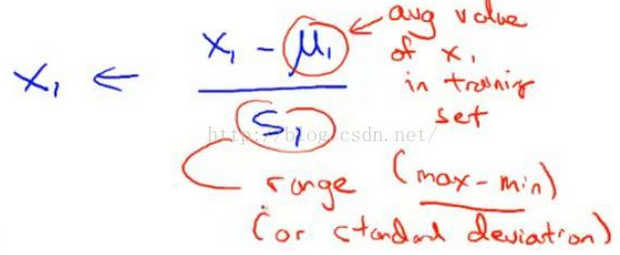
• 計算協方差矩陣
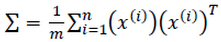
• 對協方差矩陣進行奇異值分解；
• 選取最大的前K個特征值對應的特征向量u⁽¹⁾，u⁽²⁾，u⁽³⁾，.....，u^(k)
• 輸出降維的投影特征矩陣Ureduce={u⁽¹⁾，u⁽²⁾，u⁽³⁾，.....，u^(k)}
• 輸出降維後的數據集z=Ureduce^Tx

4、選擇降維後的維度K（主成分的個數）

　　如何選擇主成分個數K呢？先來定義兩個概念：

　　選擇不同的K值，然後用下面的式子不斷計算，選取能夠滿足下列式子條件的最小K值即可。

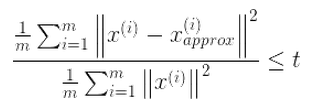
　　其中t值可以由自己定，比如t值取0.01，則代表了該PCA算法保留了99%的主要信息。當你覺得誤差需要更小，

你可以把t值設的更小。上式還可以用SVD分解時產生的S矩陣來表示，如下面的式子：

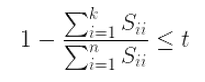
　　註意1：雖然PCA有降維的效果，也許對避免過擬合有作用，但是最好不要用PCA去作用於過擬合。

　　註意2：在訓練集中找出PCA的主成分，（可以看做為映射 mapping），然後應用到測試集和交叉驗

　　證集中。而不是對所有數據集使用PCA然後再劃分訓練集，測試集和交叉驗證集。

以上是全部內容，如果有什麽地方不對，請在下面留言，謝謝~

機器學習之PCA主成分分析