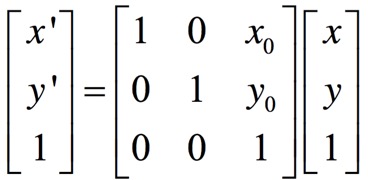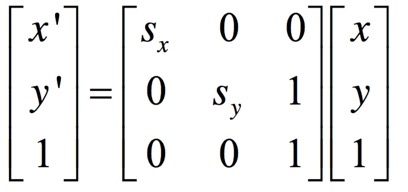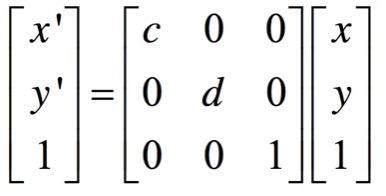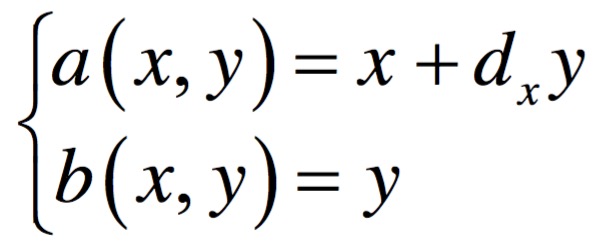接著上次的平移和映象操作，這次是縮放、旋轉和錯切操作。

話說我還從來沒在blog中放過圖片 ＝ ＝。這次順便試一下。所以先放出程式處理後的效果圖（順便把前面的映象操作的結果也放一下）。

首先是作為程式輸入的input.bmp影象：

然後是旋轉45度的結果（程式中可任意選擇旋轉角度）：

按X軸映象後的結果(可選X或Y)：

按X軸錯切20度以後的結果(可選X或Y，可選角度0~45度):

然後是X方向放大兩倍，Y方向不變的結果(可任意選擇各個方向的縮放倍數，但偏差太大的話影象效果不好):

在這篇blog裡面我就不放完整的程式碼了。。因為寫的太醜。。這五個操作全放在一起寫了500多行，太長了。

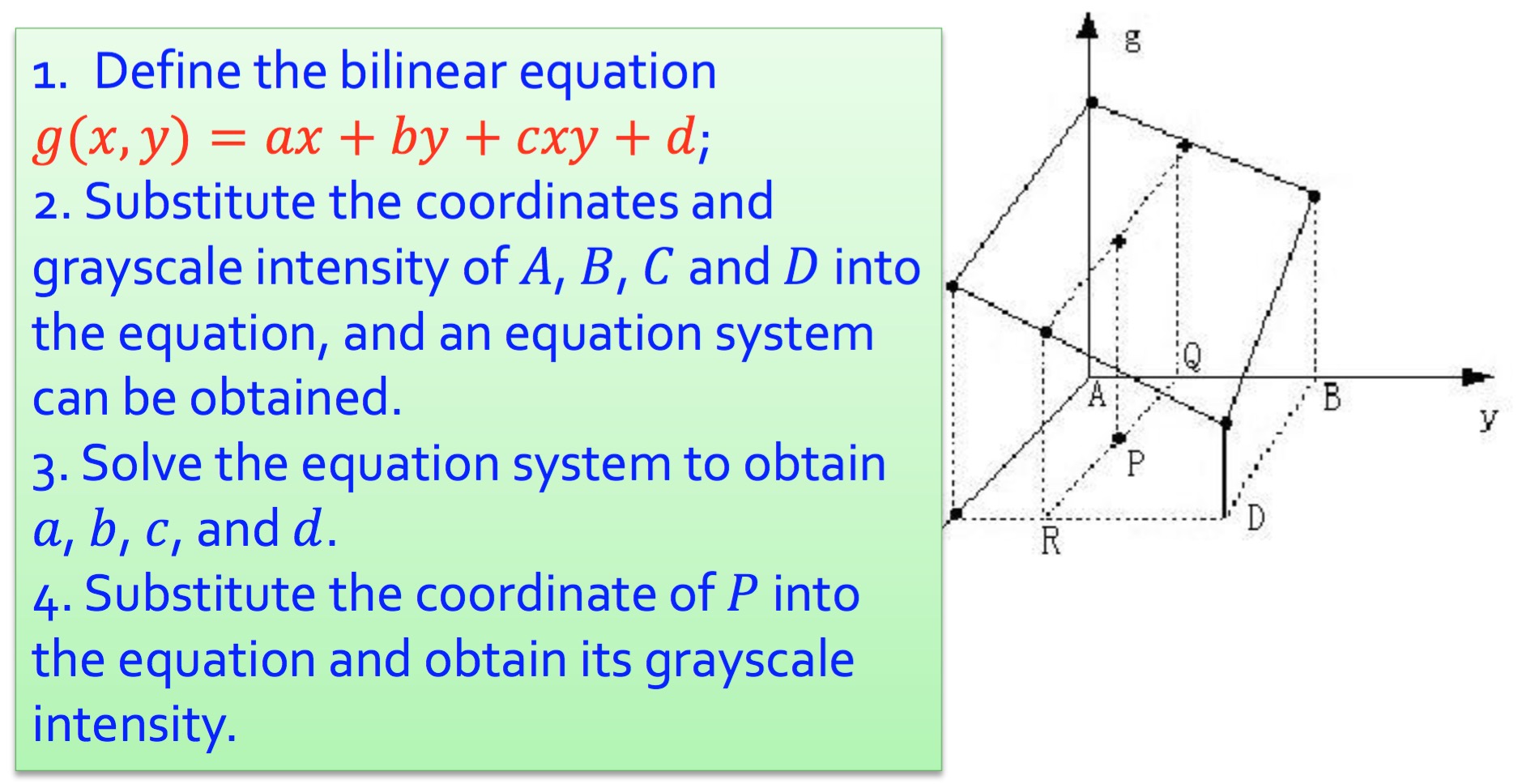
主要講一下思路吧，前面也說過，平移和映象操作比較簡單，因為無需考慮插值(interpolation)。然而如果在縮放、旋轉操作中不進行插值的話，那麼影象就會出現許多空點，比如像是這樣：

而計算插值有許多方法，比如最鄰近插值、雙線性插值、RBF插值等等。在這裡我用的是雙線性插值，因為效果尚可且操作簡單。原理如下：

也就是說，針對點P，尋找四周有值的四個點，然後計算他們的灰度值（在RGB中分別計算三通道），解方程即可。在實際操作中，可以先計算出水平方向的中間點（上圖的R，Q點）再計算P點。

再說各個操作的原理。

圖象變化其實都是對每個畫素點進行變換。都可以用矩陣的形式來表達。設某個畫素點轉變前的座標為(x, y)，轉變後的座標為(x’, y’)，那麼對於translation來說，矩陣座標變換是如下這樣的：

mirror操作的變換是這樣的：

其中，當sx＝1，sy = -1的時候就是針對x軸做映象變換，反之則是對Y軸做映象變換

scale操作的變換是這樣的：

c, d兩個值可任選，當然做完scale以後要記得interpolation

rotation：

就是根據旋轉角度進行三角變換，同樣需要interpolation

而shear就是以某一系數對單方向的畫素點進行變換，例如如果針對X軸做變換的話就是這樣：