蒙特卡羅樹搜尋+深度學習 -- AlphaGo原版論文閱讀筆記
原版論文是《Mastering the game of Go with deep neural networks and tree search》,有時間的還是建議讀一讀,沒時間的可以看看我這篇筆記湊活一下。網上有一些分析AlphaGo的文章,但最經典的肯定還是原文,還是踏踏實實搞懂AlphaGo的基本原理我們再來吹牛逼吧。
需要的一些背景
對圍棋不瞭解的,其實也不怎麼影響,因為只有feature engineering用了點圍棋的知識。這裡有一篇《九張圖告訴你圍棋到底怎麼下》可以簡單看看。
對深度學習不怎麼了解的,可以簡單當作一個黑盒演算法。但機器學習的基礎知識還是必備的。沒機器學習基礎的估計看不太懂。
“深度學習是機器學習的一種,它是一臺精密的流水線,整頭豬從這邊趕進去,香腸從那邊出來就可以了。”蒙特卡羅方法
蒙特卡羅演算法:取樣越多,越近似最優解;
拉斯維加斯演算法:取樣越多,越有機會找到最優解;
舉個例子,假如筐裡有100個蘋果,讓我每次閉眼拿1個,挑出最大的。於是我隨機拿1個,再隨機拿1個跟它比,留下大的,再隨機拿1個……我每拿一次,留下的蘋果都至少不比上次的小。拿的次數越多,挑出的蘋果就越大,但我除非拿100次,否則無法肯定挑出了最大的。這個挑蘋果的演算法,就屬於蒙特卡羅演算法——儘量找好的,但不保證是最好的。
作者:蘇椰
連結:https://www.zhihu.com/question 蒙特卡羅樹搜尋(MCTS)
網上的文章要不拿蒙特卡羅方法忽悠過去;要不籠統提一下,不提細節;要不就以為只是樹形的隨機搜尋,沒啥好談。但MCTS對於理解AlphaGo還是挺關鍵的。
MCTS這裡的取樣,是指一次從根節點到遊戲結束的路徑訪問。只要取樣次數夠多,我們可以近似知道走那條路徑比較好。貌似就是普通的蒙特卡羅方法?但對於樹型結構,解空間太大,不可能完全隨機去取樣,有額外一些細節問題要解決:分支節點怎麼選(寬度優化)?不選比較有效的分支會浪費大量的無謂搜尋。評估節點是否一定要走到底得到遊戲最終結果(深度優化)?怎麼走?隨機走?
基本的MCTS有4個步驟Selection,Expansion,Simulation,Backpropagation(論文裡是backup,還以為是備份的意思),論文裡state,action,r(reward),Q 函式都是MCTS的術語。

圖片展示瞭如何更新節點的勝率,選擇勝率大的分支進行搜尋(7/10->5/6->3/3),到了3/3葉子節點進行展開選擇一個action,然後進行模擬,評估這個action的結果。然後把結果向上回溯到根節點。來自維基百科
具體的細節,可以參考UCT(Upper Confidence Bound for Trees) algorithm – the most popular algorithm in the MCTS family。從維基百科最下方那篇論文截的圖。原文有點長,這裡點到為止,足夠理解AlphaGO即可。N是搜尋次數,控制exploitation vs. exploration。免得一直搜那個最好的分支,錯過邊上其他次優分支上的好機會。
AlphaGo
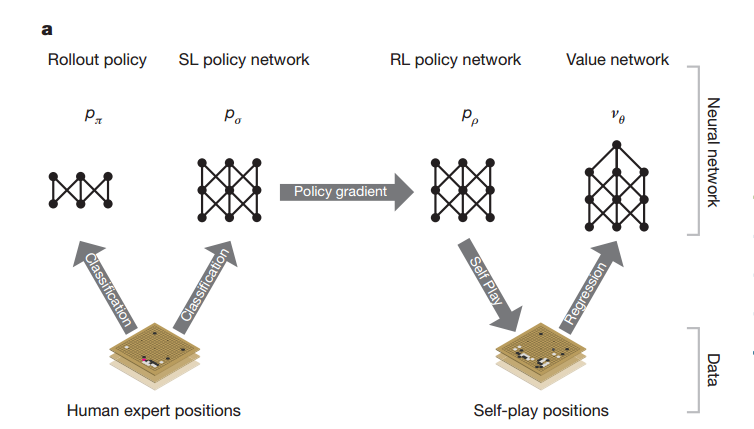
四大元件。最後只直接用了其中3個,間接用其中1個。
Policy Network (Pσ )
Supervised learning(SL)學的objective是高手在當前棋面(state)選擇的下法(action)。
要點
1. 從棋局中隨機抽取棋面(state/position)
2. 30 million positions from the KGS Go Server (KGS是一個圍棋網站)。資料可以說是核心,所以說AI戰勝人類還為時尚早,AlphaGo目前還是站在人類expert的肩膀上前進。
3. 棋盤當作19*19的黑白二值影象,然後用卷積層(13層)。比影象還好處理。rectifier nonlinearities
3. output all legal moves
4. raw input的準確率:55.7%。all input features:57.0%。後面methods有提到具體什麼特徵。需要一點圍棋知識,比如liberties是氣的意思
Fast Rollout Policy (Pπ )
linear softmax + small pattern features 。對比前面Policy Network,
- 非線性 -> 線性
- 區域性特徵 -> 全棋盤
準確率降到24.2%,但是時間3ms-> 2μs。前面MCTS提到評估的時候需要走到底,速度快的優勢就體現出來了。
Reinforcement Learning of Policy Networks (Pρ )
要點
- 前面policy networks的結果作為初始值
ρ=μ - 隨機選前面某一輪的policy network來對決,降低過擬合。
zt=±1 是最後的勝負。決出勝負之後,作為前面每一步的梯度優化方向,贏棋就增大預測的P,輸棋就減少P。- 校正最終objective是贏棋,而原始的SL Policy Networks預測的是跟expert走法一致的準確率。所以對決結果80%+勝出SL。
跟Pachi對決,勝率從原來當初SL Policy Networks的11%上升到85%,提升還是非常大的。
Reinforcement Learning of Value Networks (vθ )
判斷一個棋面,黑或白贏的概率各是多少。所以引數只有s。當然,你列舉一下a也能得到p(a|s)。不同就是能知道雙方勝率的相對值
- using policy
p for both players (區別RL Policy Network:前面隨機的一個P和最新的P對決) vθ(s)≈vPρ(s)≈v∗(s) 。v∗(s) 是理論上最優下法得到的分數。顯然不可能得到,只能用我們目前最強的Pρ 演算法來近似。但這個要走到完才知道,只好再用Value Networkvθ(s) 來學習一下了。
Δθ∝∂vθ(s)∂θ(z−vθ(s))
(上面式子應該是求min(z−vθ(s))2 ,轉成max就可以去掉求導的負號)因為前序下法是強關聯的,輸入只有一個棋子不同,z是最後結果,一直不變,所以直接這麼算會overfitting。變成直接記住結果了。解法就是隻抽取game中的position,居然生成了30 million distinct positions。那就是有這麼多局game了。
| MSE | training set | test set |
|---|---|---|
| before | 0.19 | 0.37 |
| after | 0.226 | 0.234 |
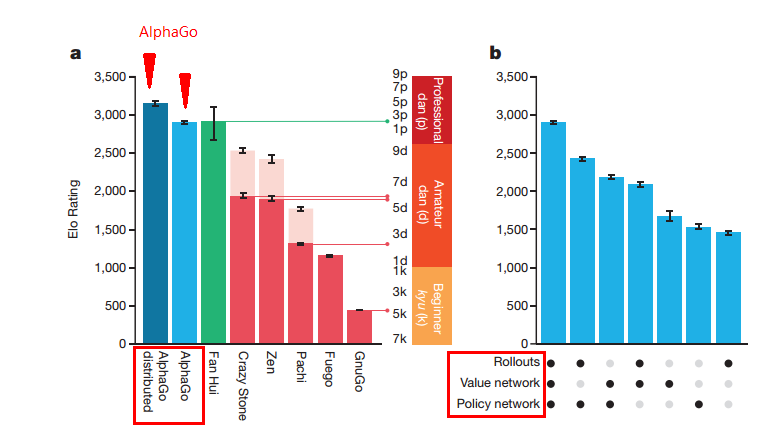
AlphaGo與其他程式的對比。AlphaGo上面提到的幾個元件之間對比。這幾個元件單獨都可以用來當AI,用MCTS組裝起來威力更強。(kyu:級,dan:段)
MCTS 組裝起來前面的元件
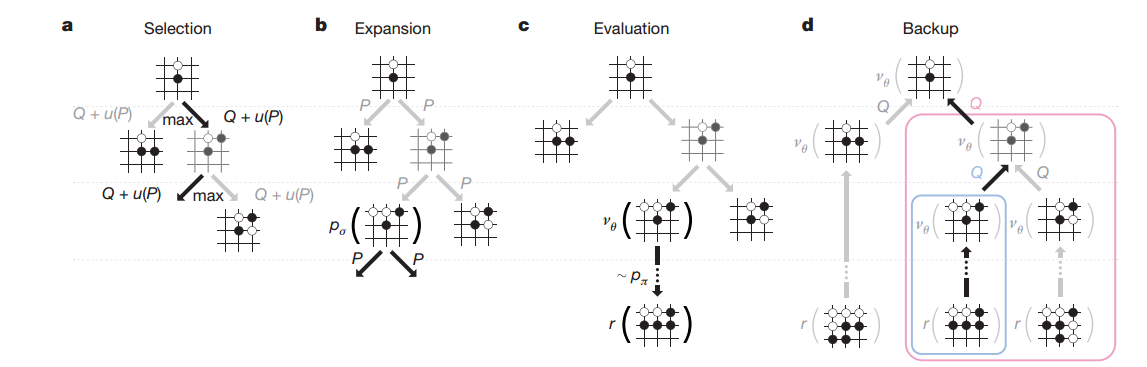
結構跟標準的MCTS類似。
每次MCTS simulation選擇
我自己補了個常數C,寫到一起容易看點。
- value network
vθ - fast rollout走到結束的結果
zL
最開始還沒expand Q是0,那SL的
for the single best move)。所以人類在這一點暫時獲勝!不過另一方面,RL學出來的value networks在評估方面效果好。所以各有所長。
搜尋次數N一多會扣分, 鼓勵exploration其他分支。
summary
整體看完,感覺AlphaGo實力還是挺強的。在機器學習系統設計和應用方面有很大的參考意義。各個元件取長補短也挺有意思。
瞭解了AlphaGo之後,再去看別人的分析就比較有感覺了,比如fb同樣弄圍棋的 @田淵棟 的 AlphaGo的分析 - 遠東軼事 - 知乎專欄