回溯法 之 馬周遊(馬跳日)問題
回溯法的應用很多,下面講述一個有趣的馬周遊問題。
馬周遊(馬跳日)問題:在一個 8*8 的棋盤上(如下圖)一匹馬從任意位置開始,恰好走過棋盤中的每一格(每個格子有且只能走一次),並且最後還可以回到起點位置。
這個問題其實可以進行推廣:即棋盤大小不一定是 8*8 ,只要棋盤大小 M * N 滿足:
① M >=6 ;N>= 6 ② M N都是偶數 ③ | M-N | <=2
當然這個問題還可以縮小:即馬周遊最後不一定要回到原點,只要遍歷走完棋盤中的所有格子即可。
顯然常規的解法就是採用回溯法,並且要在回溯過程中進行剪枝。
一、下面從馬周遊最簡單的問題描述開始做起:即馬周遊只需要遍歷走完棋盤中的所有格子即可,不要求最後要回到起點位置
解法說明:其實很容易理解到,馬周遊棋盤,也就是要遍歷棋盤中的所有格子有且只能一次,那麼很顯然就是一個圖的遍歷問題了。怎麼理解呢?
在前面的文章 八皇后 中,每個皇后都有 8 個位置的選擇,那麼對應來說就是一個滿八叉樹(也可以看做是圖)的遍歷。下面給出一個四皇后問題的圖解。在這個圖中我們就可以清楚的看到圖的遍歷過程,而且是深度優先遍歷。

那麼同樣的,關於馬周遊問題,也是同樣要進行圖的深度優先遍歷過程。那麼深度優先遍歷過程可以遞迴實現,可以非遞迴實現。下面分別給出其實現程式碼。
(1)遞迴實現
#include<iostream> #include <stdlib.h> #include <iomanip> using namespace std; //馬周遊的棋盤,注意使用的時候是從下表為1開始 int board[100][100]; int fx[]= {2,1,-1,-2,-2,-1,1,2}; int fy[]= {-1,-2,-2,-1,1,2,2,1}; int n; //棋盤大小 //引數x,y 表示棋盤的位置 //檢測(x,y) 對應位置在棋盤中是否合法 bool check(int x,int y) { if(x<1 || y<1 || x>n || y>n || board[x][y] != 0) return false; return true; } //輸出結果 void outputResult(int n) { for(int i=1; i<=n; i++) { cout<<endl<<endl; for(int j=1; j<=n; j++) { cout<<setw(3)<<board[i][j]<<" "; } } cout<<endl<<endl; } void runTable(int a,int b,int number) { if(number == n*n) //已經走完棋盤中所有的點 { outputResult(n); //輸出 exit(1); } for(int i=0; i<8; i++) //表示每一個格都有八種走法 { if(check(a + fx[i],b + fy[i])) { int x = a + fx[i]; int y = b + fy[i]; board[x][y] = number+1; //走到下一個位置,設定其序號為 number+1 runTable(x, y,number+1); board[x][y] = 0;//回溯 } } } //遞迴走法 void horseRun(int x,int y) { int number = 1; board[x][y] = number; //首先確定起始位置這個格是序號為1 runTable(x, y,number); } int main() { cout<<"輸入棋盤大小n:"; cin>>n; int x,y; cout<<"輸入馬周遊起始位置x(1~n),y(1~n):"; cin>>x>>y; horseRun(x,y); return 0; }
執行效果:

說明:以上程式在執行棋盤大小為 6*6 的時候,可以很快跑出結果,但是在棋盤大小為 8*8 的時候,就要花費幾秒,說明這個執行的效果不是很好。
(2)非遞迴實現
#include<iostream> #include <iomanip> #include <queue> using namespace std; //在某一格子的八種走法 int fx[]= {2,1,-1,-2,-2,-1,1,2}; int fy[]= {-1,-2,-2,-1,1,2,2,1}; typedef struct { int x,y; //座標 int number; //序號 } Point; //棋盤中的格子 //馬周遊的棋盤,注意使用的時候是從下表為1開始 Point board[10000][10000]; int n; //棋盤大小 int step =1; //序號 //輸出結果 void outputResult(int n) { for(int i=1; i<=n; i++) { cout<<endl<<endl; for(int j=1; j<=n; j++) { cout<<setw(3)<<board[i][j].number<<" "; } } cout<<endl<<endl; } bool check(int x,int y) { if(x<1 || y<1 || x>n || y>n || board[x][y].number != 0) return false; return true; } //下一位置有多少種走法 int nextPosHasSteps(int x, int y) { int steps = 0; for (int i = 0; i < 8; ++i) { if (check(x + fx[i], y + fy[i])) steps++; } return steps; } //非遞迴的走法 void horseRun(Point point) { queue<Point> pointQueue; pointQueue.push(point); Point temp; while(!pointQueue.empty()) { temp = pointQueue.front(); pointQueue.pop(); board[temp.x][temp.y].number = step++; int minStep = 8; int flag = 0; for(int i=0; i<8; i++) //出下一位置走法最少的進入對列 { int x=temp.x + fx[i]; int y=temp.y + fy[i]; if(check(x,y)) { if(nextPosHasSteps(x,y) <= minStep) { minStep = nextPosHasSteps(x,y); Point t; t.x = x; t.y = y; if(flag) pointQueue.pop(); pointQueue.push(t); flag = 1; } } } } } int main() { cout<<"輸入棋盤大小n:"; cin>>n; Point startPoint; cout<<"輸入馬周遊起始位置x(1~n),y(1~n):"; cin>>startPoint.x>>startPoint.y; horseRun(startPoint); //輸出結果 outputResult(n); return 0; }
說明:在程式中已經用到了一個剪枝:即每一次都優先走下一位置走法最少的。 關於剪枝的內容下面會具體講述。
執行效果:
說明:此種解法可以很快的跑出結果,甚至在 幾千乘以幾千的棋盤中,都是幾乎瞬間跑出結果,效果十分的好,因為這裡面用了一個很關鍵的剪枝。
二、完整解決馬周遊問題:既要遍歷走完棋盤中所有的格子,最後還要回到起點。
有了上面第一個簡化版馬周遊的解決經驗,那麼完整解決馬周遊問題,無法就是再新增一個限制條件:最後要回到起點。
那麼首先還是要先介紹一下在這個馬周遊回溯過程中要用到的剪枝(如果不用剪枝,那麼演算法執行效率會很低)。
使用剪枝有3處:
1、使用Warnsdorff's rule。在當前位置(Now)考慮下一個位置(Next)的時候,優先選擇下一個的位置(Next)走法最少的那個。作為當前位置(Now)的下一位置(Next)。
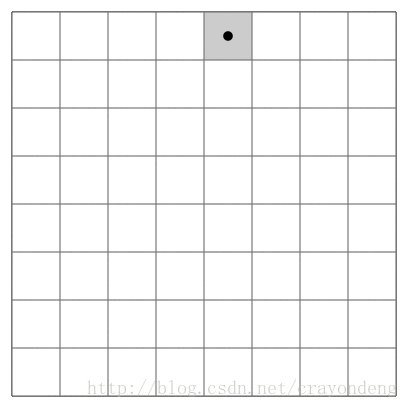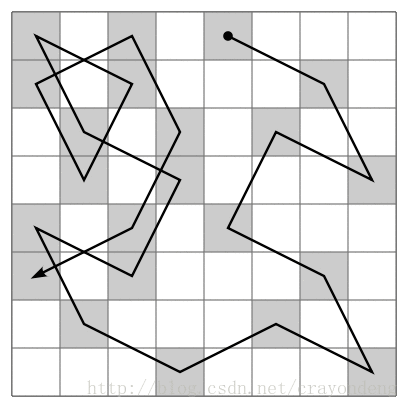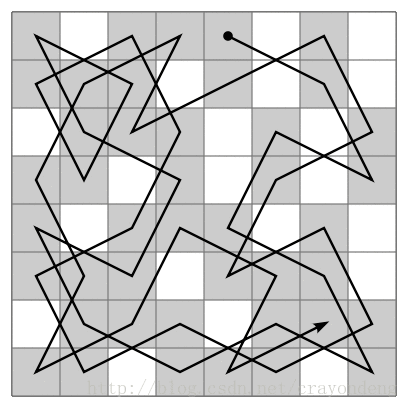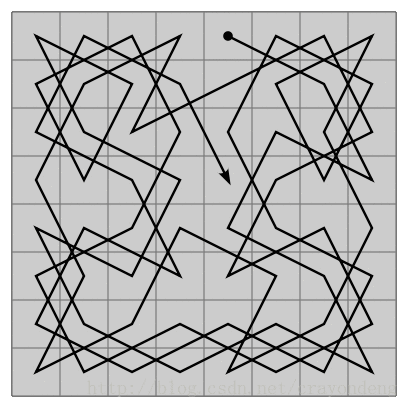
譬如說:下圖所示,當前位置現在要確定下一位置,那麼就要所有的下一個位置進行考察,看看假如走到下一個位置,它的下一個位置又有多少種走法,選擇下一個位置可能走法最少的作為當前位置(Now)的下一個位置(Next)。
2、在進行了第一點的剪枝後,如果可以優先選擇的下一個位置不止一個,則優先選擇離中心位置較遠的位置作為下一步(即靠近邊邊的位置)。
通俗點理解,第一點的剪枝就是走那些位置可能走到機會比較小的,反正走到的機會小,那麼先走完總是好的,要不然你兜一圈回來,還是要走這一個位置的。
第二點的剪枝就是走法儘量從邊邊走,然後是往中間靠。
3、第三點的剪枝,每次都從棋盤的中間點開始出發,然後求出一條合法路徑後再平移映射回待求路徑。
怎麼理解呢?所謂馬周遊棋盤,最後還要回到起點。也就是在棋盤中找到一條哈密頓迴路。那麼不管你是從哪裡開始的,最後都是會在這個哈密頓迴路中的,那麼選取的中點的位置也肯定是在這個迴路上的。
最後,找到這個這個以中點為起點的哈密頓迴路後,根據設定起點在這個迴路中的序號,映射回以這個位置為起點的馬周遊路線即可。
至於為什麼要從棋盤中間位置開始呢? 我就不太能解釋了。
知道了上面的三種剪枝方式,那麼具體是要如何實現的呢?
(1)關於第一點和第二點的剪枝,二者關聯很大。那麼我們可以將二者結合起來。放到一個結構體中,這個結構體表徵是的是下一位置。
typedef struct NextPos
{
int nextPosSteps; //表示下一位置有多少種走法;走法少的優先考慮
int nextPosDirection; //下一位置相對於當前位置的方位
int nextPosToMidLength; //表示當前位置距中間點距離;距離中間點遠的優先考慮
//
bool operator < (const NextPos &a) const
{
return nextPosSteps > a.nextPosSteps && nextPosToMidLength < a.nextPosToMidLength;
}
};注意其中,下一位置走法少的優先,下一位置距離中點遠的優先。
這樣我們在挑選下一個位置的時候,可以將符合要求的放到一個優先佇列中,這樣選取下一位置的時候直接從優先佇列拿出了就好了(省去排序的工作)。
(2)關於第三點的剪枝,其實就是涉及到最後輸出結果,這個比較簡單。
下面完整給出程式碼實現:
#include <iostream>
#include <stdlib.h>
#include <iomanip>
#include <queue>
using namespace std;
typedef struct
{
int x;
int y;
} Step;
Step step[8] = { {-2, -1}, {-1, -2}, { 1, -2}, { 2, -1}, { 2, 1}, { 1, 2}, {-1, 2}, {-2,1} };
typedef struct NextPos
{
int nextPosSteps; //表示下一位置有多少種走法;走法少的優先考慮
int nextPosDirection; //下一位置相對於當前位置的方位
int nextPosToMidLength; //表示當前位置距中間點距離;距離中間點遠的優先考慮
//
bool operator < (const NextPos &a) const
{
return nextPosSteps > a.nextPosSteps && nextPosToMidLength < a.nextPosToMidLength;
}
};
int board[100][100];
int M,N; //棋盤大小
//檢測這個位置是否可以走
bool check(int x, int y)
{
if (x >= 0 && x < M && y >= 0 && y < N && board[x][y] == 0)
return true;
return false;
}
//下一位置有多少種走法
int nextPosHasSteps(int x, int y)
{
int steps = 0;
for (int i = 0; i < 8; ++i)
{
if (check(x + step[i].x, y + step[i].y))
steps++;
}
return steps;
}
//判斷是否回到起點
bool returnStart(int x, int y)
{
//校驗最後是否可以回到起點,也就是棋盤的中間位置
int midx,midy;
midx = M / 2 - 1;
midy = N / 2 - 1;
for (int i = 0; i < 8; ++i)
if (x + step[i].x == midx && y + step[i].y == midy)
return true;
return false;
}
//輸出結果
void outputResult(int xstart,int ystart)
{
int num = M * N;
int k = num - board[xstart][ystart];
for (int i = 0; i < M; ++i)
{
cout<<endl<<endl;
for (int j = 0; j < N; ++j)
{
board[i][j] = (board[i][j] + k) % num + 1;
cout<<setw(5)<<board[i][j];
}
}
cout<<endl<<endl;
}
//某一位置距離棋盤中心的距離
int posToMidLength(int x,int y)
{
int midx = M / 2 - 1;
int midy = N / 2 - 1;
return (abs(x - midx) + abs(y - midy));
}
void BackTrace(int t, int x, int y,int xstart,int ystart)
{
//找到結果
if (t == M * N && returnStart(x,y)) //遍歷了棋盤的所以位置,並且最後可以回到起點,形成迴路
{
outputResult(xstart,ystart);
exit(1);
}
else
{
priority_queue<NextPos> nextPosQueue;
for (int i = 0; i < 8; ++i)
{
if (check(x + step[i].x, y + step[i].y))
{
NextPos aNextPos;
aNextPos.nextPosSteps = nextPosHasSteps(x + step[i].x, y + step[i].y);
aNextPos.nextPosDirection = i;
aNextPos.nextPosToMidLength = posToMidLength(x + step[i].x,y + step[i].y);
nextPosQueue.push(aNextPos);
}
}
while(nextPosQueue.size())
{
int d = nextPosQueue.top().nextPosDirection;
nextPosQueue.pop();
x += step[d].x;
y += step[d].y;
board[x][y] = t + 1;
BackTrace(t + 1, x, y,xstart,ystart);
//回溯
board[x][y] = 0;
x -= step[d].x;
y -= step[d].y;
}
}
}
void horseRun(int xstart,int ystart)
{
//初始化棋盤
for (int i = 0; i < M; i++)
for (int j = 0; j < N; j++)
board[i][j] = 0;
int midx = M / 2 -1;
int midy = N / 2 -1;
board[midx][midy] = 1; //從棋盤的中間的位置開始馬周遊
BackTrace(1, midx, midy,xstart,ystart);
}
int main(void)
{
//馬周遊起始位置
int x, y;
cout<<"請輸入棋盤大小m*n|m-n|<=2 且 m和n都為偶數 且 m,n < 20 :";
cin>>M>>N;
cout<<"請輸入馬周遊起始位置--橫縱座標0 <= x < "<<M<<"和0 <= y < "<<N<<" :";
cin>>x>>y;
horseRun(x,y); //執行馬周遊
return 0;
}執行效果:
說明:這個程式的極限是 20 ,當棋盤大小達到 20 * 20 的時候就很難跑出結果,但是小於20的棋盤都可以很快的跑出結果。
好了,關於馬周遊問題就講述到這裡,歡迎交流討論。