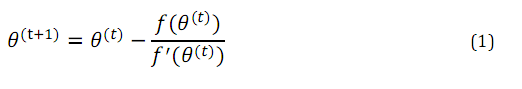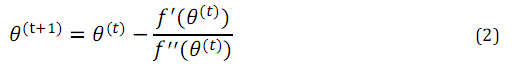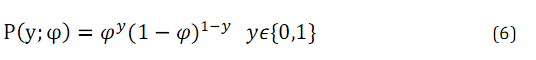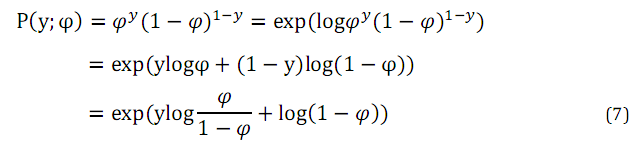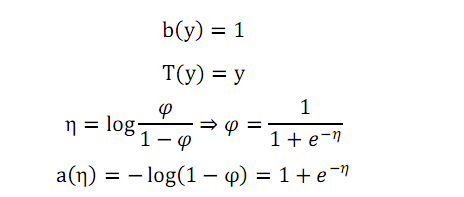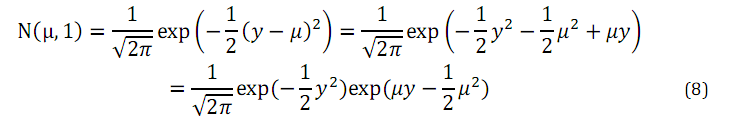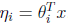斯坦福大學公開課機器學習課程(Andrew Ng)四牛頓方法與廣義線性模型
本次課所講主要內容:
1、 牛頓方法:對Logistic模型進行擬合
2、 指數分佈族
3、 廣義線性模型(GLM):聯絡Logistic迴歸和最小二乘模型
一、牛頓方法
牛頓方法與梯度下降法的功能一樣,都是對解空間進行搜尋的方法。
假設有函式

步驟:
1)
給出一個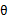
2)
在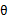

3)
令x軸交點處為新的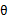
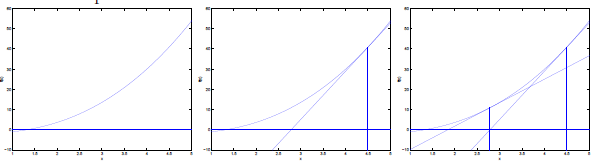
如下圖所示:
因為過





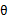


所以更新規則為:
牛頓方法在機器學習中的應用
對於機器學習問題,我們優化的目標函式為極大似然估計L,當極大似然估計函式取值最大時,其導數為0,這樣就和上面函式f取0的問題一致了。
極大似然函式的求解更新規則為:
牛頓方法的收斂速度:二次收斂
每次迭代使解的有效數字的數目加倍:假設當前誤差是0.1,一次迭代後,誤差為0.001,再一次迭代,誤差為0.0000001。該性質當解距離最優質的足夠近才會發現。
上面是當引數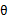
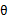
H為Hessian矩陣,後面的是目標函式的梯度。H的規模是n*n,n為引數向量的長度,它的每個元素表示一個二階導數,計算公式如下:
牛頓方法的優缺點:
優點:若特徵數和樣本數合理,牛頓方法的迭代次數比梯度上升要少得多
缺點:每次迭代都要重新計算Hessian矩陣,如果特徵很多,則H矩陣計算代價很大
二、指數分佈族
指數分佈族是指可以表示為指數形式的概率分佈。指數分佈的形式如下:
η - 自然引數,通常是一個實數
T(y) – 充分統計量,通常,T(y)=y,實際上是一個概率分佈的充分統計量(統計學知識)
當a、b、T都給定時,上式定義了一個以η為引數的函式族。
下面我們將伯努利分佈與高斯分佈轉換為指數分佈族的形式。
伯努利分佈
對其進行如下轉換:
有公式(7),對比公式(5),我們就可以分別得到公式(5)中各引數,如下:
由上式可以發現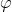
高斯分佈的形式為
高斯分佈轉換為指數分佈的推導過程如下:
有公式(8)可知,高斯分佈轉換為指數分佈族的引數分別為:
三、廣義線性模型
定義了指數分佈族之後有什麼用呢?我們可以通過指數分佈族引出廣義線性模型(generalized linear model, GLM)。
在統計學上,廣義線性模型是一種受到廣泛應用的線性迴歸模式。此模式假設實驗者所量測的隨機變數的分佈函式與實驗中系統性效應(即非隨機的效應)可經由一連結函式(link function)建立起可資解釋其相關性的函式。
注意到上述公式7與公式8的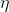
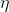
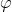
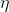
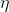
廣義線性模型有三個假設:
(1)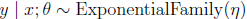
例:若要統計網站點選量y,用泊松分佈建模
(2) 給定x,目標是求出以x為條件的T(y)的期望E[T(y)|x],即讓學習演算法輸出h(x) = E[T(y)|x]
(3)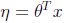
logistic模型的推導如下:
在這個式子中,第一行是伯努利分佈的性質,第二行有假設二和假設三得出。
最小二乘模型的推導如下:
正則響應函式:g(η) = E[y;η],將自然引數η和原始概率分佈中的引數聯絡起來的函式
正則關聯函式:g-1
總結:廣義線性模型通過假設一個概率分佈,得到不同模型,例如當選取高斯分佈時,就可以得到最小二乘模型,當選取伯努利分佈時就得到logistic模型,而梯度下降、牛頓方法都是為了求取使所建立模型有最優解的未知引數 。
。參考:
斯坦福ML公開課筆記
http://blog.csdn.net/maverick1990/article/details/12564973