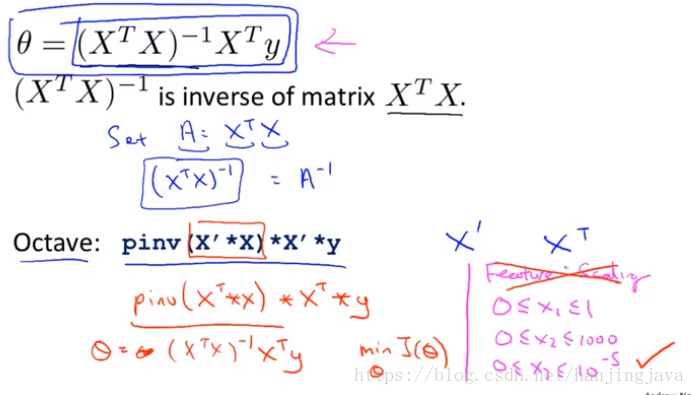本文是學習Andrew Ng的機器學習系列教程的學習筆記。教學視訊地址：

本文中的白色背景視訊截圖來自Andrew Ng的視訊腳程, 思維導圖為原創總結。

多變數的線性迴歸：

15. Linear Regression with multiple variables - multiple features 首先定義出線性迴歸的矩陣表示：  

Use vector to show feature

Inner product(內積) is θ transpose X

Feature vector X

Parameter vector theta θ

Multivariate linear regression

16. Linear Regression with multiple variables - Gradient descent for multiple variables然後是梯度下降的矩陣表示：

就是對各個特徵求偏導，不包含求導引數時，導數都為0.  

17. Linear Regression with multiple variables - Gradient descent in practice I : feature scaling  

Feature scaling 特徵縮放

Y = θ1 * x1 + θ2 * x2

If x1 = 0-2000, x2 = 1-5, then when

Use feature scaling to get more effect Gradient Descent.

Feature scaling make x1 and x2 be closer. Then the gradient descent will converge much faster.

Dividing by the maximum value

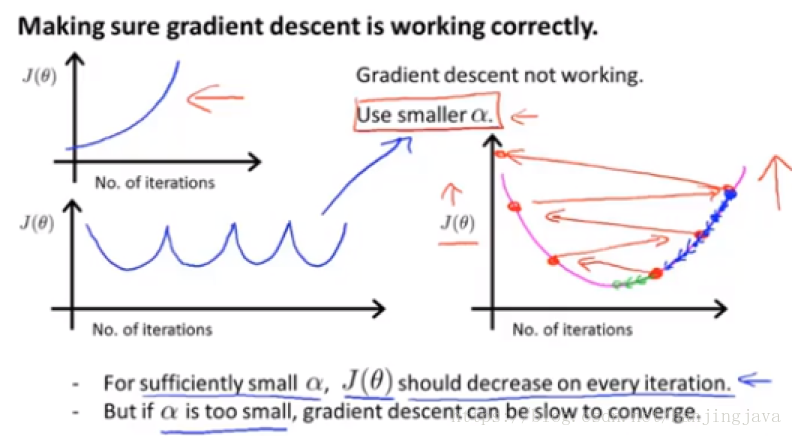
18. Linear regression with multiple variables - gradient descent in practive II: learning rate 用圖形化方法來檢視選擇的學習率引數合不合適，每次可以按3倍的關係調整學習率。這裡要不斷嘗試，沒有絕對方法。

J(θ) should decease after each iterations

After 400 iterations, the gradient descent is already converge.

Choosing what this threshold is pretty difficult.

So, in order to check your gradient descent has converged, I actually tend to look at plots like this figure. And this figure will tell you if your gradient descent is working correctly.

When you see this figure, thy to use small learning rate

Choose more α  to try.

Choose a small one and then increase the learning rate threefold.

Many times later, you will get one value that is too small and one value is too large.

Then I try to pick the largest possible value or just something slightly smaller than the largest reasonable value that I found. This may be a good learning rate for my problem.

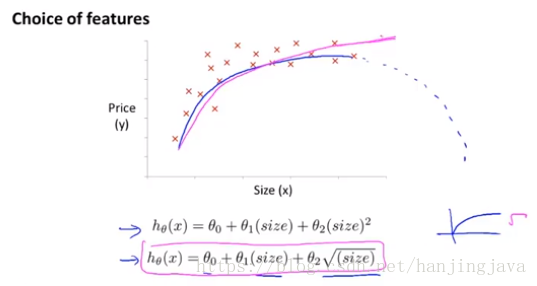
19. Linear regression with multiple variables - features and polynomial regression 

How to choose features and algorithm

Polynomial regression allows you to use the machinery of linear regression to fit very complicated, even very non-linear functions.

Two features times together or add higher ^

Not use frontage and depth, but use land area = frontage * depth.

Feature scaling will more important when use polynomial regression

Choose different features you can sometimes get better models.

Find better models to fit your data.

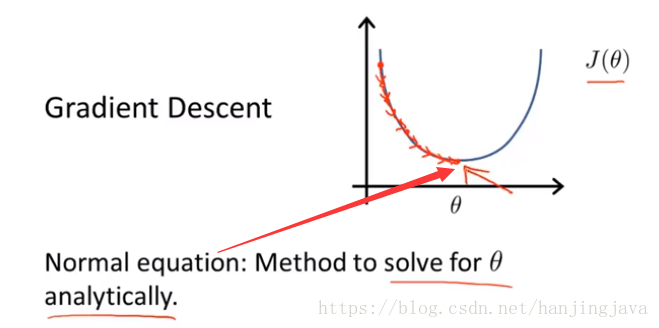
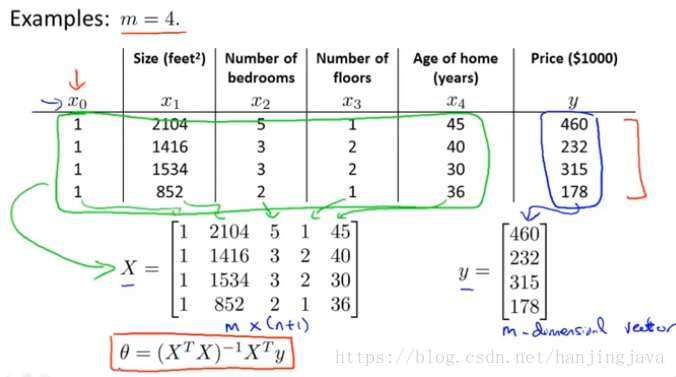
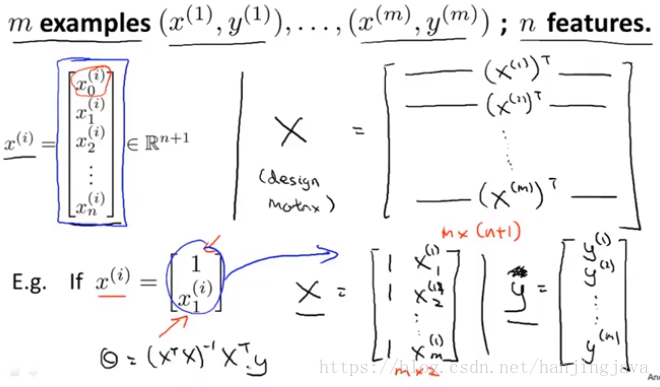
20. Linear regression with multiple variables - normal equation 用公式來計算引數：  

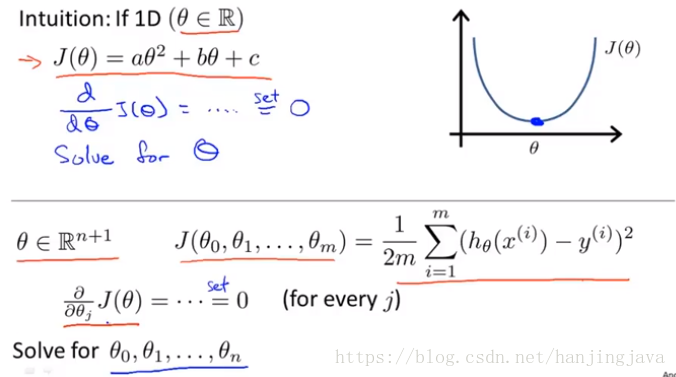
Normal equation can get the optimal value θ in basically one step.

Calculus tell us how to find better through take the partial derivative of J.

Normal equation:

And if you use normal equation there is no need to features scaling.

When number of features is large, use Gradient Descent.

When get non-invertibility X^TX, how to use normal equation.

When features have linear relations, the X^TX will be non-invertible.