在機器人的運動中，經常會涉及到航向推演。 下面這篇部落格寫的挺好的。

在學習機器人運動模型推導的時候，有看到 網上別人的推導過程，連結如下：

其中都有相對應的推導過程，但是，如果我只是在這 複製黏貼那就毫無意義了，這裡說一下我的推導思路，沒有做對應的近似，

結果也是很接近，算是開拓思路，減少誤差吧，找個時間將會 搭個機器人里程計 框架計算出結果再與imu對比， 看一下誤差會不會特別大。

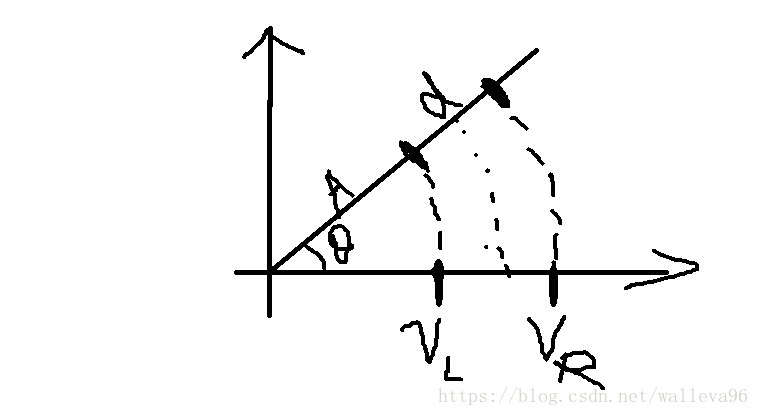
哈哈，感受一下靈魂畫手吧。 在差速機器人模型中，應用 PID（或ADRC演算法）的演算法，對左右輪的電機進行閉環控制，可以得到一個相對比較穩定的轉速狀態，設左路的速度為Vl 右輪為Vr, 那麼模型的中心線的線速度 Va=(Vl+Vr)/2 , 旋轉角為θ， 左輪離圓心的距離為A，右輪離圓心的距離為（A+d）， 輪距為d，設運動的時間Δt。

那麼可得左輪的旋轉角的公式為 ： θ/360‘= （Δt * Vl）/（2*π*A），右輪的公式為 ： θ/360‘= （Δt * Vr）/（2*π*（A+d）），

將二者相等之後，可得： A = （Vl*d）/（Vr-Vl），

模型的中線點的線速度和角度的公式為：  θ/360‘ = （Va*Δt）/（2*π*（A+d/2））；

結合前面的等式可得：  θ/360‘= （(Vr-Vl) *Δt ）/（2*π*d） ;

所以      θ = （(Vr-Vl) *Δt *360 ）/（2*π*d） ; 弧度制：  θ = （(Vr-Vl) *Δt ）/（d），

這公式打得累死，===

前面的連結上 都會利用 泰勒級數，對 sin（θ ）===》 θ。

如有錯誤，歡迎指出。

最後感謝一下csdn的草稿儲存，差點哭出來 ==