做機器人底層程式的時候，經常用到航跡推演（Odometry），無論是定位導航還是普通的方向控制。航跡推演中除了對機器人位姿進行估計，另一個很重要的關係是移動機器人前進速度、轉向角速度與左輪速度、右輪速度之間的轉換。

  在機器人區域性路徑規劃演算法DWA解析一文中，是在假設已知機器人前進線速度和角速度的情況下，對機器人航跡推演的位姿進行推導了，然而缺少如何通過左右輪速度得到、，因此本文將補上這個空缺。

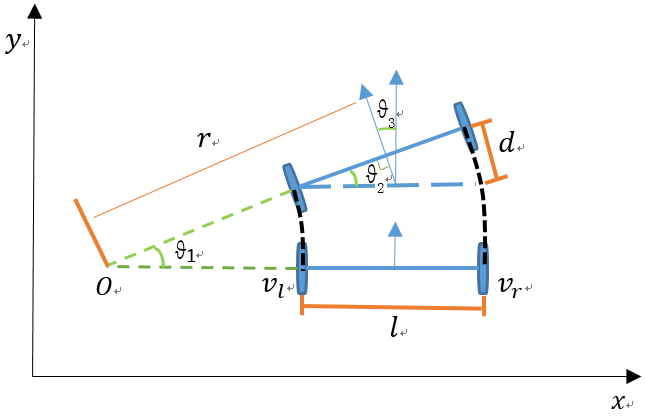
  下圖是移動機器人在兩個相鄰時刻的位姿，其中是兩相鄰時刻移動機器人繞圓弧運動的角度，是兩相鄰時刻移動機器航向角（朝向角head）的變化量。是左右輪之間的間距，是右輪比左輪多走的距離。

  移動機器人前進速度等於左右輪速度的平均，這個好理解。

         (1)

  現在來推導機器人航向角如何計算，以及如何計算角速度。如圖所示，把兩個時刻的機器人位置疊加在一起，可以清楚的看到移動機器人航向角變化量是。從圖中的幾何關係可以得到：

也就是說移動機器人航向角變化了多少角度，它就繞其運動軌跡的圓心旋轉了多少角度。這句話很好驗證，我們讓機器人做圓周運動，從起點出發繞圓心一圈回到起點處，在這過程中機器人累計的航向角為360度，同時它也確實繞軌跡圓心運動了360度，說明機器人航向角變化多少度，就繞圓心旋轉了多少度。而這三個角度中，

所以可以得到機器人繞圓心運動的角速度，它也是機器人航向角變化的速度：

        (2)

線速度、角速度都有了，因此可以推出移動機器人圓弧運動的半徑：

       (3)

從公式（3）可以發現當左輪速度等於右輪速度時，半徑無窮大，即直線運動。最後將三個公式綜合起來，可以得到左右輪速度和線速度角速度之間的關係如下，：