移動機器人相機模型:從相機移動到二維影象
阿新 • • 發佈:2020-10-04
如果只是希望獲取影象上的一些資訊(例如特徵提取、擬合等),那麼我們不會對三維空間中相機的位置有所要求。但如果希望通過二維的影象去理解三維空間中攝像機的資訊,或者是影象中物體在三維空間中的資訊,那麼就不得不考慮成像過程中三維變化為二維時的具體過程。而攝像機模型就是三維到二維的一種對映。本文簡要總結了**單目相機**的成像過程,以便於讀者將相機模型作為一種基礎的工具理解更深層次的內容。
本文通過講解三維世界座標系下某一點是如何被對映到二維影象上的一點的完整流程來講解,以下為整體流程:
$$
World\ \to Camera\ \to Retinal\ \to Pixel\
$$
(世界座標系——相機座標系——成像平面座標系——影象座標系)
下面對這四個座標系作出一個簡要的介紹:
- 世界座標系` P_w`:通常是三維空間中人為選擇的一個參考座標系。單位為物理單位,例如m。
- 相機座標系` P_c`:三維空間中,通常以攝像機的光心作為原點,光軸作為z軸的一個座標系。可以通過世界座標系的平移和旋轉來獲得。單位為物理單位,例如m。
- 成像平面座標系` P`:通過相機模型對映得到的一個二維座標系。單位為物理單位,例如m。
- 影象座標系` P_uv`:通過所成像轉換獲得的在計算機內部可以儲存的矩陣影象上的座標系。單位為畫素。
## 1. World -> Camera
**假如攝像頭固定不動,那麼世界座標系和相機座標系可以直接重合。但如果我們要把攝像頭放在一個能夠移動的機器人身上,那麼就有必要令一個固定的座標系和一個跟著機器人走的相機座標系。**
如果上述這句話你不太理解,那就說明你確實有必要閱讀這篇文章,等到閱讀結束後再回過頭來思考這個問題。而現在,你只需要知道,我們在這裡考慮的是後面這種情況,即**攝像頭置於移動機器人上**。
作為一個移動機器人,它必然有所處位置座標和一個朝向,我們把機器人的位置和朝向稱為**位姿**。如果它還沒開始運動,我們不妨將該位置作為世界座標系原點,而相機朝向作為Z軸:
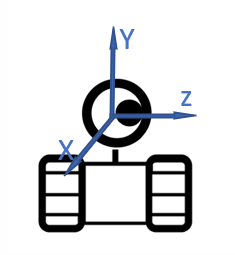
機器人在空間中會進行移動和轉向,於是我們可以按照同樣方式定義一個跟隨著機器人進行移動的座標系,稱為相機座標系。
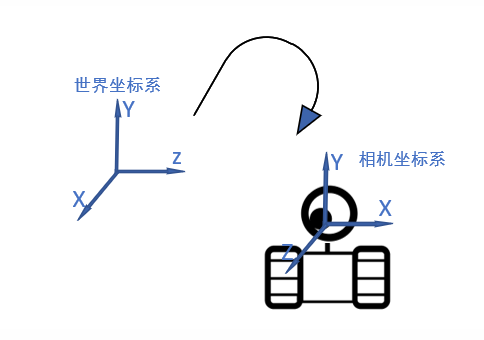
為了表示出這種移動和轉向,我們需要知道機器人相對於原來位置移動了多少,旋轉了多少。
很自然的,我們可以通過當前機器人在世界座標系下的座標,來表示機器人是如何從世界座標系原點移動到當前位置。於是把該座標,稱為**平移向量**:
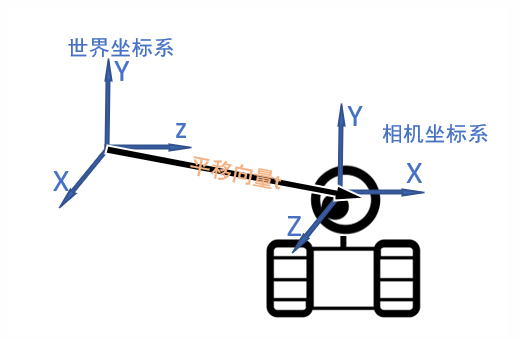
而對於**旋轉**,通常使用旋轉矩陣R進行描述。對於如何理解旋轉矩陣,我這裡推薦看[臺大的機器人學視訊P4](https://www.bilibili.com/video/BV1v4411H7ez?p=4)(通過列空間變換和投影的方式去理解)。我這裡直接使用單位正交基的方式進行描述,意思是一致的。總之,下式表示是**在A看來B座標系的姿態**,或者可以把在B座標系下的座標表示通過左乘下列R轉換成A座標系下的座標表示。
$$
R_{AB}=\begin{bmatrix} |&|&|\\\hat X_B^A & \hat Y_B^A & \hat Z_B^A\\ |&|&|\\\end{bmatrix}=\begin{bmatrix}e_1^Ae_1^B & e_2^Ae_1^B & e_3^Ae_1^B\\ e_1^Ae_2^B & e_2^Ae_2^B & e_3^Ae_2^B\\e_1^Ae_3^B & e_2^Ae_3^B & e_3^Ae_3^B\\ \end{bmatrix}
$$
也就是說,旋轉矩陣R除了表示在A看來B座標系的姿態,也可以**用來轉換空間中某一點的座標表示**(而這正是我們的相機模型最需要的)。即有:
$$
P^A=R_{AB}P^B
$$
此外在機器人學中比較重要的一點是,R能夠用來描述物體的旋轉。例如下式就表示的是在A座標系下點1通過一個R旋轉至點2。
$$
P_2^A=RP_1^A
$$
回到我們的機器人上來。假定現在機器人在世界座標系初始位置時看到了一點` P_W`,然後經過一次旋轉和平移,此時看到了同一個點,座標為` P_C`。通過上面的定義,我們能夠很自然的得到一個等式:
$$
P_c=R_{cw}P_w+t_{cw}
$$
我們通常把這裡的` R`和` t`稱為**相機的外參**。
為了矩陣運算上的便利,上式同時也可以表現成下面這樣(注意使用的是齊次座標的形式):
$$
\begin{bmatrix}
x_w\\y_w\\z_w\\1
\end{bmatrix}
=
\begin{bmatrix}
R & t \\ 0^t & 1
\end{bmatrix}
\begin{bmatrix}
x_c\\y_c\\z_c\\1
\end{bmatrix}
$$
常將中間由R和t組成的矩陣寫作變換矩陣T,於是可以表示成下列形式:
$$
P_c=T_{cw}P_w \ldots\ldots0
$$
此式子即為世界座標系轉換為相機座標系的變換式。它揭示了兩個很簡單的道理:1. 知道` R_cw`和` t_cw`,那就能夠將點在兩個座標系下進行轉換。2. 如果知道多個點在兩個座標系下的座標表示,那就可以求解獲得` R_cw`和` t_cw`。
## 2. Camera -> Retinal
好了,現在我們已經能夠知道如何把世界座標系下的點轉換成相機座標系下的點了,現在我們要考慮的是三位空間下的點是如何轉換到二維平面上。此刻我們考慮的幾何模型才是真正的相機模型。
相機模型通常會考慮兩種:**針孔模型**和**透鏡模型。**
一般來說,考慮針孔模型就夠了,因為透鏡模型不過是將針孔模型的焦距f進行修改。
首先先考慮針孔模型([圖源](https://raw.githubusercontent.com/CV-xueba/A01_cvclass_basic/master/%E8%AE%A1%E7%AE%97%E6%9C%BA%E8%A7%86%E8%A7%89%E5%9F%BA%E7%A1%80_%E8%AF%BE%E4%BB%B6/12_%E6%91%84%E5%83%8F%E6%9C%BA%E5%87%A0%E4%BD%95.pdf)):
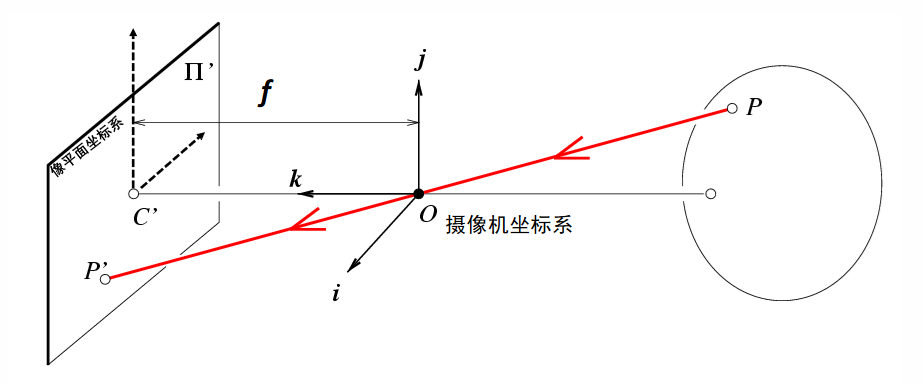
如上圖所示,針孔模型可以簡單看作,位於三維空間中的某一點P經過相機座標系的中心點O對映至像平面座標系上的P'的一個過程。於是乎,我們可以把這一模型視作一個相似三角形模型:
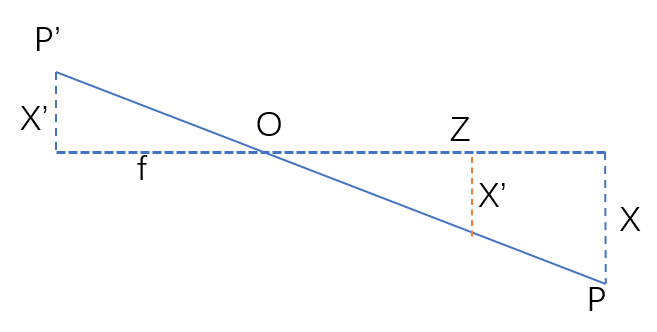
很容易看出來左邊X成像是倒的,對於座標系來說這樣的倒會引入負號,因此我們在O點右側也畫一個X‘,這樣就能消除這個負號。而對於引入的橙色X’所在平面,我們稱為歸一化成像平面。於是成像過程就有如下式子:
$$
X' = f \cfrac {X_c} {Z_c} \ldots \ldots 1
$$
$$
Y' = f \cfrac {Y_c} {Z_c}\ldots\ldots 2
$$
## 3. Retinal -> Pixel
由上面的推導,我們很清楚,它們都是在物理層面進行轉換的,因此單位都是m。而真正拿到我們手中的是一張張由畫素點構成的矩陣影象。因此在成像平面座標系到影象座標系還需要進行取樣和量化。而同時我們也清楚,影象座標的原點通常在影象左上角,x軸朝向影象右邊,y軸豎直向下。而成像平面座標系的原點則是在像的中間。因此要把成像平面座標系轉換至畫素座標系,需要**進行一次縮放和原點平移**。
因此,成像平面座標系的座標P’到畫素座標[u,v]有如下關係:
$$
u = aX'+c_x\ldots\ldots3
$$
$$
v = aY'+c_y\ldots\ldots4
$$
------
至此,我們已經完成了每一個區域性過程的推導。但是,我們不可能每次都這樣一次一次進行部分運算,如果我們希望直接把相機座標系下的點轉換到畫素座標系下,該怎麼轉換?又或者,我們希望從世界座標系下的點開始轉換呢?下面就會對這樣的過程進行講解。
## Camera -> Pixel
在上面,我們已經獲得了` Camera -> Retinal`和` Retinal -> Pixel`的式子,因此可以將` X',Y'`消去(即把1和2帶入3和4),得到下列式子:
$$
u = af \cfrac {X_c} {Z_c}+c_x
$$
$$
v = bf \cfrac {Y_c} {Z_c}+c_y
$$
通常地,我們會令` f_x = af`和`f_y = bf`(這是由於a的單位為pixel/m,而f的單位為m,相乘從而將量綱統一到pixel):
$$
u = f_x \cfrac {X_c} {Z_c}+c_x
$$
$$
v = f_y \cfrac {Y_c} {Z_c}+c_y
$$
將上式化作矩陣形式:
$$
\begin{bmatrix}
u\\v\\1
\end{bmatrix}
=
\frac 1 {Z_c}
\begin{bmatrix}
f_x & 0 & c_x \\ 0 & f_x & c_y \\ 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
X_c\\Y_c\\Z_c
\end{bmatrix}\ldots\ldots5
$$
通常我們會將中間的3*3矩陣作為**內參矩陣K**,我們很清楚,前面的f是固定的,a是取樣過程固定的,因此f_x也是固定的,也就是說內參矩陣K也是從出廠開始就是固定的:
$$
K =
\begin{bmatrix}
f_x & 0 & c_x \\ 0 & f_x & c_y \\ 0 & 0 & 1
\end{bmatrix}
$$
5式通常又可以寫作下列形式:
$$
ZP_{uv} = KP_c\ldots\ldots6
$$
## World -> Pixel
由於我們的機器人的運動,導致相機也不斷在運動,因此我們可以把0式代入到6式中:
$$
ZP_{uv}=KT_{cw}P_w
$$
至此,我們已經完成了整個過程的
