算法系列之七:愛因斯坦的思考題(上)
(1)、英國人住在紅色的房子裡;
(2)、瑞典人養狗作為寵物;
(3)、丹麥人喝茶;
(4)、綠房子緊挨著白房子,在白房子的左邊;
(5)、綠房子的主人喝咖啡;
(6)、抽Pall Mall牌香菸的人養鳥;
(7)、黃色房子裡的人抽Dunhill牌香菸;
(8)、住在中間那個房子裡的人喝牛奶;
(9)、挪威人住在第一個房子裡面;
(10)、抽Blends牌香菸的人和養貓的人相鄰;
(11)、養馬的人和抽Dunhill牌香菸的人相鄰;
(12)、抽BlueMaster牌香菸的人和啤酒;
(13)、德國人抽Prince牌香菸;
(14)、挪威人和住在藍房子的人相鄰;
(15)、抽Blends牌香菸的人和喝礦泉水的人相鄰。
這個題目的答案就包含在5個種類共25個元素的所有組合當中,當某一個組合能夠滿足以上15條線索時,就可以從中找到答案,以下就是一個滿足全部線索的組合,可以看出本題的答案是住在綠色房子中的德國人養魚作為寵物:
|
房子 |
國家 |
飲料 |
寵物 |
煙 |
|
黃色 |
挪威 |
水 |
貓 |
Dunhill |
|
藍色 |
丹麥 |
茶 |
馬 |
Blends |
|
紅色 |
英國 |
牛奶 |
鳥 |
PallMall |
|
綠色 |
德國 |
咖啡 |
魚 |
Prince |
|
白色 |
瑞士 |
啤酒 |
狗 |
BlueMaster |
用計算機解決這個問題的本質就是列舉這5個種類25個元素的所有組合,應用15條線索對每個組合進行判斷,能夠滿足全部線索的組合就是最終的結果。和其它用窮舉法演算法一樣,解決這個推理題也需要解決三個關鍵點:定義能夠描述這個問題的資料模型、基於這個資料模型的一套列舉演算法和應用15條線索判斷結果是否正確的方法。
考察這個問題的描述,需要列舉結果的元素分為5個類別,分別是房子(顏色)、國家、飲料型別、寵物種類和香菸的品牌。根據題意,5個種類的元素不能重複,但是彼此存在聯絡,這個聯絡簡單描述就是:某個國家的人只能住在某個顏色的房子中,喝一種飲料,養一種寵物並抽一種品牌的香菸。定義資料模型時可以採用“組”(group)的概念來定義這種關係,每個“組”包含5個種類的各一個元素,保證了對上述固定關係的約束。每個元素都由兩個屬性,一個是型別,一個是值,比如“咖啡”,其型別是飲料,值是咖啡,可以這樣對元素進行定義:
|
61 typedefstruct tagItem 62 { 63 ITEM_TYPE type; 64 int value; 65 }ITEM; |
確定了元素的資料定義,“組”的資料定義就可以確定了:
|
107 typedefstruct tagGroup 108 { 109 ITEM items[GROUPS_ITEMS]; 110 }GROUP; |
這個GROUP的資料定義雖然清晰明瞭,但是對GROUP內的元素的定位不是很直觀,比如對GROUP內的某個元素操作時需要遍歷所有的元素逐個比較型別來定位元素,這就存在一個演算法的效率問題。既然GROUP內的item用陣列進行組織,而陣列的下標天生就具有位置關係,何不利用這一點簡化資料定義呢?首先對ITEM_TYPE的值進行一些約束,為每個型別賦一個明確的值,這個值就是item資料的位置,固定了值之後的ITEM_TYPE定義如下:
|
42 typedefenum tagItemType 43 { 44 type_house = 0, 45 type_nation = 1, 46 type_drink = 2, 47 type_pet = 3, 48 type_cigaret = 4 49 }ITEM_TYPE; |
對GROUP也重新定義:
|
107 typedefstruct tagGroup 108 { 109 int itemValue[GROUPS_ITEMS]; 110 }GROUP; |
這樣定義GROUP可以顯著簡化資料定位問題,比如“住在中間那個房子裡的人喝牛奶”這個線索,就可以這樣用程式碼實現:
|
groups[2].itemValue[type_drink]= DRINK_MILK; |
接下來要處理15條線索的數學模型問題。先分析一下這15條線索,大致可以分成三類:第一類是描述某些元素之間具有固定繫結關係的線索,比如,“丹麥人喝茶”和“住綠房子的人喝咖啡”等等,線索1、2、3、5、6、7、12、13可歸為此類;第二類是描述某些元素型別所在的“組”所具有的相鄰關係的線索,比如,“養馬的人和抽Dunhill牌香菸的人相鄰”和“抽Blends牌香菸的人和養貓的人相鄰”等等,線索10、11、14、15可歸為此類;第三類就是不能描述元素之間固定關係或關係比較弱的線索,比如,“綠房子緊挨著白房子,在白房子的左邊”和“住在中間那個房子裡的人喝牛奶”等等。
對於第一類具有繫結關係的線索,其數學模型可以這樣定義:
|
67 typedefstruct tagBind 68 { 69 ITEM_TYPE first_type; 70 int first_val; 71 ITEM_TYPE second_type; 72 int second_val; 73 }BIND; |
first_type和first_val是一個繫結關係中前一個元素的型別和值,second_type和second_val是繫結關係中後一個元素的型別和值。以線索6“綠房子的主人喝咖啡”為例,first_type就是type_house,first_val就是COLOR_GREEN(COLOR_GREEN是個整數型常量),second_type就是type_drink,second_val就是DRINK_COFFEE(DRINK_COFFEE是個整數型常量)。線索1、2、3、5、6、7、12、13就可以儲存在binds陣列中:
|
75 const BIND binds[]= 76 { 77 { type_house, COLOR_RED, type_nation, NATION_ENGLAND}, 78 { type_nation, NATION_SWEDEND, type_pet, PET_DOG}, 79 { type_nation, NATION_DANMARK, type_drink, DRINK_TEA}, 80 { type_house, COLOR_GREEN, type_drink, DRINK_COFFEE}, 81 { type_cigaret, CIGARET_PALLMALL, type_pet, PET_BIRD}, 82 { type_house, COLOR_YELLOW, type_cigaret, CIGARET_DUNHILL}, 83 { type_cigaret, CIGARET_BLUEMASTER, type_drink, DRINK_BEER}, 84 { type_nation, NATION_GERMANY, type_cigaret, CIGARET_PRINCE} 85 }; |
對於第二類描述元素所在的“組”具有相鄰關係的線索,其數學模型可以這樣定義:
|
89 typedefstruct tagRelation 90 { 91 ITEM_TYPE type; 92 int val; 93 ITEM_TYPE relation_type; 94 int relation_val; 95 }RELATION; |
type和val是某個“組”內的某個元素的型別和值,relation_type和relation_val是與該元素所在的“組”相鄰的“組”中與之有關係的元素的型別和值。以線索10“抽Blends牌香菸的人和養貓的人相鄰”為例,type就是type_cigaret,val就是CIGARET_BLENDS(CIGARET_BLENDS是個整數型常量),relation_type是type_pet,relation_val是PET_CAT(PET_CAT是個整數型常量)。線索10、11、14、15就可以儲存在relations陣列中:
|
097 const RELATION relations[]= 098 { 099 { type_cigaret, CIGARET_BLENDS, type_pet, PET_CAT}, 100 { type_pet, PET_HORSE, type_cigaret, CIGARET_DUNHILL}, 101 { type_nation, NATION_NORWAY, type_house, COLOR_BLUE}, 102 { type_cigaret, CIGARET_BLENDS, type_drink, DRINK_WATER} 103 }; |
對於第三類線索,無法建立統一的數學模型,只能在列舉演算法進行過程中直接使用它們過濾掉一些不符合條件的組合結果。比如線索8“住在中間那個房子裡的人喝牛奶”,就是對每個飲料型別組合結果直接判斷groups[2].itemValue[type_drink]的值是否等於 DRINK_MILK,如果不滿足這個線索就不再繼續下一個元素型別的列舉。再比如線索4“綠房子緊挨著白房子,在白房子的左邊”,就是在對房子型別進行組合排列時,將綠房子和白房子看成一個整體進行排列組合的列舉,得到的結果直接符合了線索4的要求。
解決了資料模型的定義,接下來就要考慮如何判定一個組合結果符合題目要求的全部線索。這個判別是關鍵點,如果不能正確地從上億個組合結果中識別出正確的結果,後面將要介紹的列舉演算法就成了無的放失。根據本文建立的數學模型,第三類線索直接在列舉演算法部分應用,因此只需要對列舉得到的組合結果應用第一類線索和第二類線索進行過濾即可。
具有繫結關係的線索描述的是一個“組”內兩種元素之間的固定關係,判斷的方法就是遍歷全部的“組”,找到BIND資料中的first_type和first_val標識的元素所在的組group,然後檢查group組中型別為second_type的元素的值是否等於second_val,如果group中型別為second_type對應元素的值與second_val的值不一致就直接返回檢查失敗,否則就說明當前的組合結果滿足此BIND資料對應的線索,然後對下一個BIND資料重複上述檢查過程,直到檢查完binds陣列中所有線索對應的BIND資料。圖(1)是具有繫結關係的線索檢查流程圖:
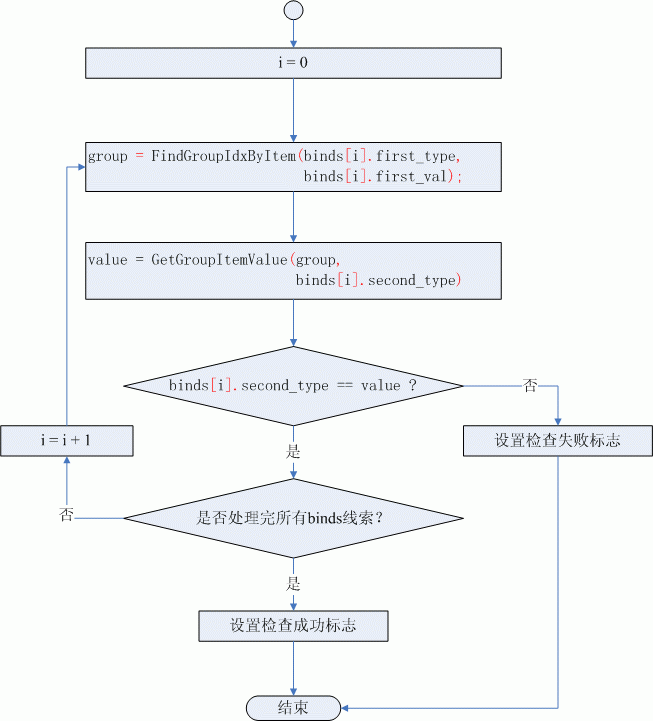
圖(1)具有繫結關係的線索檢查流程圖
“組”相鄰關係的線索描述的是相鄰的兩個組之間元素的固定關係,判斷的方法就是遍歷全部的“組”,找到RELATION資料中的type和val標識的元素所在的組group,然後分別檢查與group相鄰的兩個組(第一個組和最後一個組只有一個相鄰的組)中型別為relation_type的元素對應的值是否等於relation_val,如果相鄰的組中沒有一個能滿足RELATION資料就表示當前組合結果不滿足線索,直接返回檢查失敗。相鄰的組中只要一個組中的元素滿足RELATION資料描述的關係就表示當前組合結果符合RELATION資料對應的線索,需要對下一個RELATION資料重複上述檢查過程,直到檢查完relations陣列中的全部線索對應的RELATION資料。圖(2)是具有“組”相鄰關係的線索檢查流程圖:
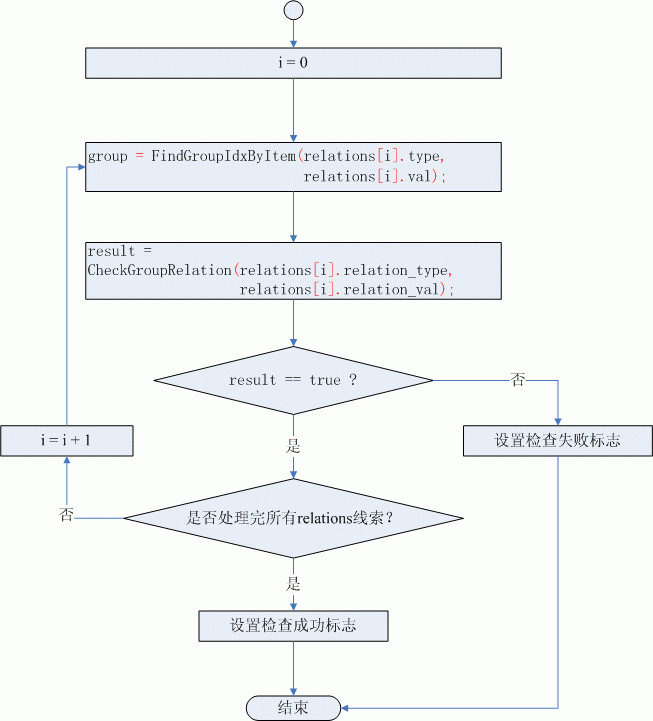
圖(2)“組”相鄰關係的線索檢查流程圖
【未完,“算法系列之七:愛因斯坦的思考題(下)”繼續】