貪心與動態規劃的區別與聯絡
先來看一個例子:
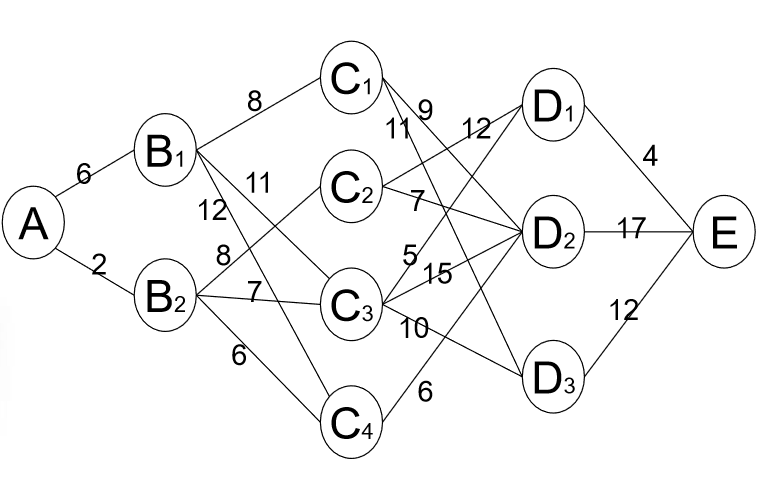
如圖,各結 點代表城市, 兩結點間連 線上數字表 示城市間的 距離。試找出從結點A到 結點E的最短距離
貪心:
首先,這題如果用貪心來看的話,則為A->B2,B2->C4, C4->D2, D2->E, 這應該沒有爭議吧(如果硬要挑毛病的話那麼就假設是有向圖,只能往右走),這樣得出來的結果是31,這是貪心的結果,即每次考慮眼前的最優解。
動態規劃:
如果從動歸的角度來看的話,那麼它的選擇就不是線性的了,而是在到達B、C、D、E這四個階段時從前面記錄的所有相鄰節點所記錄的最短路徑中選擇下一條最短路徑(總結得過於繁瑣),怎麼理解呢?我們一步步來看。
我們從A開始,在貪心和動歸眼裡都是兩條路,但不同的是貪心選擇了A->B2這條最短路徑,就遺忘了還有A->B1這個選擇,那麼它的下一步就只能從B2這個節點開始選擇下一步的最短路徑;而對於動態規劃來說,它需要記錄的不是從A開始的下一條最短路徑,它要記錄的是到從A開始的到B1所走過的最短距離和到B2所走過的最短距離,即B1=6,B2=2;然後下一步,進入到第二階段,即從B開始,它首先從B1開始,走向C1,然後記錄到C1的最短距離,即C1=8,然後是C3=17,C4=13;然後從B2開始走,C2=10,然後到C3的時候發現以前的值(即從B1到C3)比現在的大,進行更新(如果比現在的路徑距離小則跳過,也就是說對於每個格子要有一句判斷語句,判斷當前值與過去的值)即C3=9,同理C4=8;然後進入C階段
8
6 10 14
最後形成這樣一記錄表格:0 17 18 由此我們可知,最短距離就是E處記錄的值18;
2 9 19
8
因此,我們可以看出貪心與動歸的本質區別,貪心記錄眼前最優值,而動歸記錄到達每個位置時的值,而且是到達每個位置時的最優值,為什麼不漏掉某個位置呢,因為沒人會直到全域性最優路徑會不會是從這條路走出來的。
請注意我上面說的這句話,它暗含的意思是從區域性最優不一定能推出全域性最優,同時也表明了貪心不一定能算出全域性最優。而動歸是全域性的最優解。
(下面的內容經我檢查,發現有誤,請勿輕易閱讀!!!!!!,但未查明原因,故尚未刪除)
下面就動歸的問題,我有些其他的思考:
計算矩陣連乘積:
在科學計算中經常要計算矩陣的乘積。若A是一個p×q 的矩陣,B是一個q×r的矩陣,則其乘積C=AB是一個 p×r的矩陣。計算C=AB總共需要pqr次的乘法。現在 的問題是,給定n個矩陣{A1,A2,…,An}。其中Ai與Ai+1是 可乘的,i=1,2,…,n-1。要求計算出這n個矩陣的連乘積 A1A2…An
看一個計算3個矩陣{A1,A2,A3}的連乘積的例子。設3個 矩陣的維數:10×100,100×5和5×50。按 ((A1A2)A3) 算,需10×100×5+10×5×50=7500次乘法。若按 (A1(A2A3))算,則需要的乘法次數為 100×5×50+10×100×50=75000
下面是上課時老師給出的關於動態規劃解矩陣連乘積問題的思路
記矩陣連乘積AiAi+1…Aj為Ai…j,設計算次序在矩陣Ak和Ak+1之間將矩陣鏈斷開, 1<=k<n,則完全加括號方式為((A1…Ak) (Ak+1…An)) 先計算A1…k和Ak+1…n,然後將所得的結果相乘才 得到A1…n。顯然其總計算量為計算A1…k的計算量 加上計算Ak+1…n的計算量,再加上A1…k與Ak+1…n 相乘的計算量 關鍵特徵是:計算A1…n的一個最優次序所包含的 計算A1…k和Ak+1…n的次序也是最優的
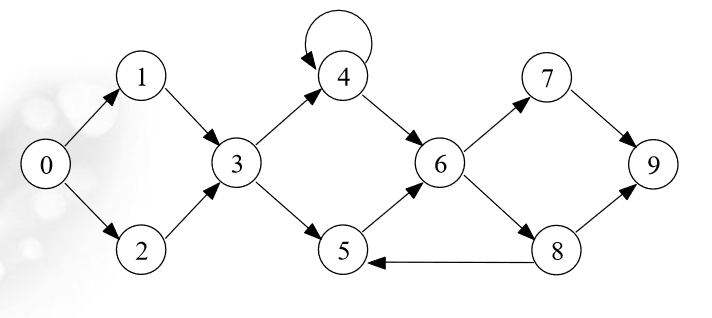
這裡說到A1...Aj可以分解為A1...Ak和Ak+1...Aj,這似乎與我前面說的有些出入,因為這裡暗含的意思是區域性最優可以推出全域性最優,那麼怎麼回事呢?請注意思路中所說, 對於矩陣來說,它的總計算量是等於分段的計算量相乘的, 也就是說在這裡相當於單一的路徑,請看下面的圖:
(沒找到合適的圖,暫且用這張,假設為有權圖,即每條邊都有權值,設為長度),如果要求求出從0到9的最短距離,那麼很明顯,點0,3,6,9是必經點,在這幾個點上,貪心的結論是成立的,即0->9的最短路徑可以分為幾段路徑之和,但對於其他點來說,這一結論是不成立的,因為最短路徑不一定會經過那個點。同樣,對於本文一開始給出的那張圖來說,結論可謂是處處不成立,因為除了兩端點每個點都是分裂點。(這僅是我在老師講解動態規劃舉矩陣連乘時產生的思考,本人水平不高,如若有錯,敬請指正,謝謝)