第四講——Neural Networks 神經網路的表示

===============================

（一）、為什麼引入神經網路？——Nonlinear hypothesis

（二）、神經元與大腦（Neurons and Brain）

（三）、神經網路的表示形式

（四）、怎樣用神經網路實現邏輯表示式？

（五）、分類問題（Classification）

本章主要圍繞神經網路的建模及其線性表示（即neural networks的representation）做以初步瞭解，在下一章中將會有更詳細的神經網路如何學習方面的知識。

===============================

（一）、為什麼引入神經網路？——Nonlinear hypothesis

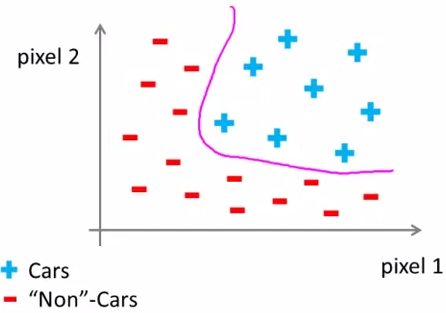
之前我們討論的ML問題中，主要針對Regression做了分析，其中採用梯度下降法進行引數更新。然而其可行性基於假設引數不多，如果引數多起來了怎麼辦呢？比如下圖中這個例子：從100*100個pixels中選出所有XiXj作為logistic regression的一個引數，那麼總共就有5*10^7個feature，即x有這麼多維。

所以引入了Nonlinear hypothesis，應對高維資料和非線性的hypothesis（如下圖所示）：

===============================

（二）、神經元與大腦（neurons and brain）

神經元工作模式：

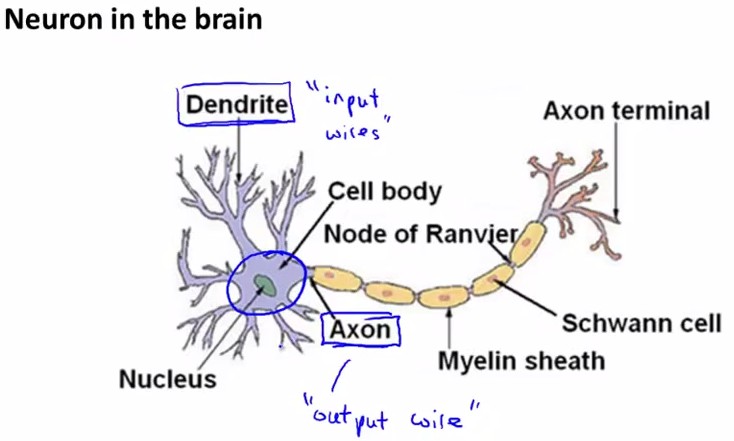
神經網路的邏輯單元：輸入向量x（input layer），中間層a(2,i)（hidden layer）, 輸出層h(x)（output layer）。

其中，中間層的a(2,i)中的2表示第二個級別（第一個級別是輸入層），i表示中間層的第幾個元素。或者可以說，a(j,i) is the activation of unit i in layer j.

===============================

（三）、神經網路的表示形式

從圖中可知，中間層a(2，j)是輸入層線性組合的sigmod值，輸出又是中間層線性組合的sigmod值。

下面我們進行神經網路引數計算的向量化：

令z⁽²⁾表示中間層，x表示輸入層，則有

，

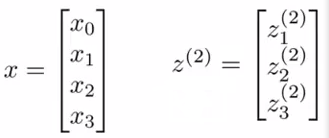z⁽²⁾=Θ⁽¹⁾x

a⁽²⁾=g(z⁽²⁾)

或者可以將x表示成a⁽¹⁾，那麼對於輸入層a⁽¹⁾有[x_0~x_3]4個元素，中間層a⁽²⁾有[a⁽²⁾₀~a⁽²⁾₃]4個元素（其中令a⁽²⁾₀=1），則有

h(x)= a⁽³⁾=g(z⁽³⁾)

z⁽³⁾=Θ⁽²⁾a⁽²⁾

通過以上這種神經元的傳遞方式（input->activation->output）來計算h(x), 叫做Forward propagation, 向前傳遞。

這裡我們可以發現，其實神經網路就像是logistic regression，只不過我們把logistic regression中的輸入向量[x₁~x₃]變成了中間層的[a⁽²⁾₁~a⁽²⁾₃], 即

h(x)=g(Θ⁽²⁾₀ a⁽²⁾₀+Θ⁽²⁾₁ a⁽²⁾₁+Θ⁽²⁾₂ a⁽²⁾₂+Θ⁽²⁾₃ a⁽²⁾₃)

而中間層又由真正的輸入向量通過Θ⁽¹⁾學習而來，這裡呢，就解放了輸入層，換言之輸入層可以是original input data的任何線性組合甚至是多項式組合如set x1*x2 as original x1...另外呢，具體怎樣利用中間層進行更新下面會更詳細地講；此外，還有一些其他模型，比如：

===============================

（四）、怎樣用神經網路實現邏輯表示式？

神經網路中，單層神經元（無中間層）的計算可用來表示邏輯運算，比如邏輯AND、邏輯或OR

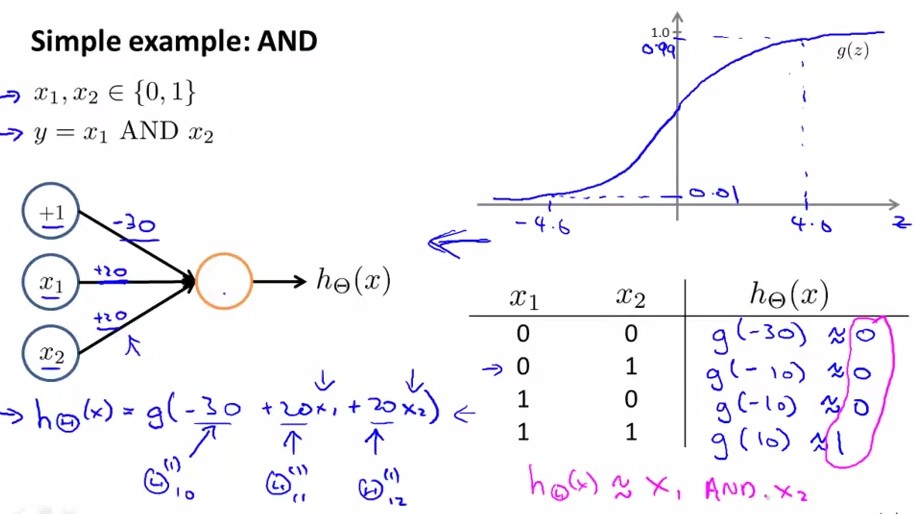
給定神經網路的權值就可以根據真值表判斷該函式的作用。再給出一個邏輯或的例子，如下圖所示：

以上兩個例子只是單層傳遞，下面我們再給出一個更復雜的例子，用來實現邏輯表達< x1 XNOR x2 >, 即邏輯同或關係，它由前面幾個例子共同實現：

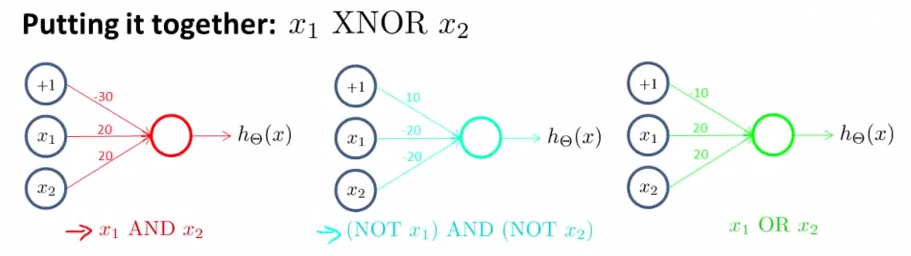
將AND、NOT AND和 OR分別放在下圖中輸入層和輸出層的位置，即可得到x1 XNOR x2，道理顯而易見：

a²₁ = x1 && x2

a²₂ = （﹁x1）&&（﹁x2） 

a³₁ =a²₁ ||a²₁ =(x1 && x2) ||  （﹁x1）&&（﹁x2） = x1 XNOR x2；

應用：手寫識別系統

===============================

（五）、分類問題（Classification）

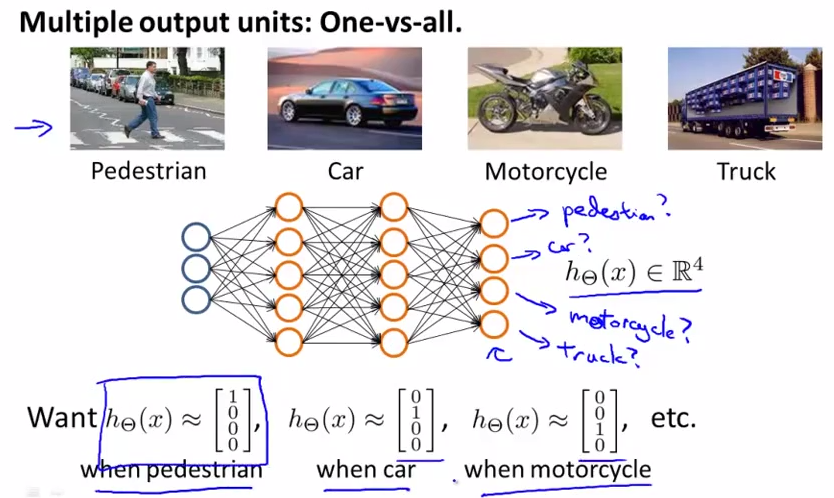
輸入向量x有三個維度，兩個中間層，輸出層4個神經元分別用來表示4類，也就是每一個數據在輸出層都會出現[a b c d]^T，且a,b,c,d中僅有一個為1，表示當前類。