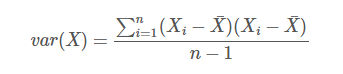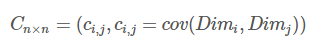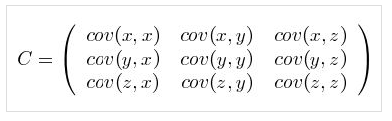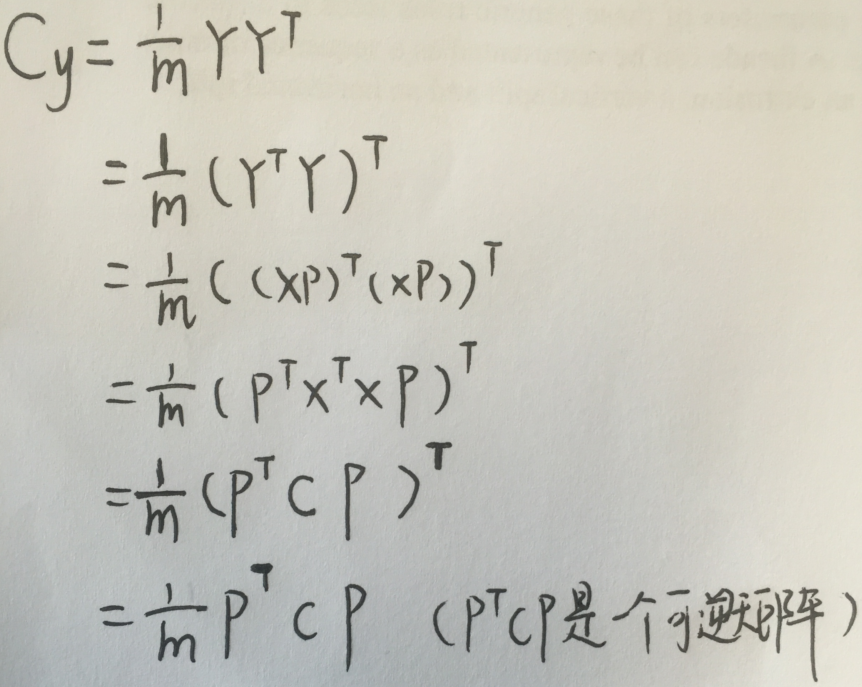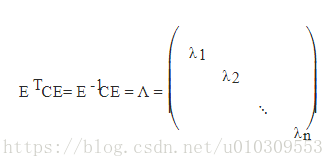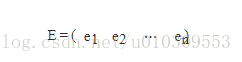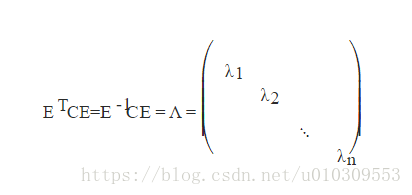一、協方差矩陣

一個維度上方差的定義：

協方差的定義：

（a）

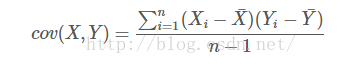
協方差就是計算了兩個維度之間的相關性，即這個樣本的這兩個維度之間有沒有關係。

協方差為0，證明這兩個維度之間沒有關係，協方差為正，兩個正相關，為負則負相關。

協方差矩陣的定義：

對n個維度，任意兩個維度都計算一個協方差，組成矩陣，定義如下

直觀的對於一個含有x,y,z三個維度的樣本，協方差矩陣如下

可以看出，對角線表示了樣本在在各個維度上的方差。

其他元素表示了不同維度之間兩兩的關聯關係。

二、協方差矩陣的計算

（1）先讓樣本矩陣中心化，即每一維度減去該維度的均值，使每一維度上的均值為0，

（2）然後直接用新的到的樣本矩陣乘上它的轉置

（3）然後除以(N-1)即可‘

數學推導相對容易，樣本矩陣中心化以後，樣本均值為0，因此式a中每個維度無需減去均值，只需要進行與其他維度的乘法，

這樣就可以用轉置相乘實現任意兩兩維度的相乘。

三、矩陣相乘的“變換的本質”理解

A*B兩個矩陣相乘代表什麼？

A的每一行所表示的向量，變到B的所有列向量為基底表示的空間中去，得到的每一行的新的表示。

B的每一列所表示的向量，變到A的所有行向量為基底表示的空間中去，得到的每一列的新的表示。

三、PCA深入

PCA的目的是降噪和去冗餘，是一種常用的資料分析方法。PCA通過線性變換將原始資料變換為一組各維度線性無關的表示，可用於提取資料的主要特徵分量，常用於高維資料的降維。

樣本矩陣的格式：

樣本1 [特徵a1，特徵a2，特徵a3，.....，特徵an]

樣本2 [特徵a1，特徵a2，特徵a3，.....，特徵an]

樣本3 [特徵a1，特徵a2，特徵a3，.....，特徵an]

樣本4 [特徵a1，特徵a2，特徵a3，.....，特徵an]

PCA後：r<n

樣本1 [特徵b1，特徵b2，特徵b3，.....，特徵br]

樣本2 [特徵b1，特徵b2，特徵b3，.....，特徵br]

樣本3 [特徵b1，特徵b2，特徵b3，.....，特徵br]

樣本4 [特徵b1，特徵b2，特徵b3，.....，特徵br]

直白的來說，就是對一個樣本矩陣，

（1）換特徵，找一組新的特徵來重新表示

（2）減少特徵，新特徵的數目要遠小於原特徵的數目

我們來看矩陣相乘的本質，用新的基底去表示老向量，這不就是重新找一組特徵來表示老樣本嗎？？？

所以我們的目的是什麼？就是找一個新的矩陣（也就是一組基底的合集），讓樣本矩陣乘以這個矩陣，實現換特徵+減少特徵的重新表示。

因此我們進行PCA的基本要求是：

（1）第一個要求：使得樣本在選擇的基底上儘可能的而分散。

為什麼這樣？

極限法，如果在這個基底上不分散，乾脆就在這個基地上的投影(也就是特徵)是一樣的。那麼會有什麼情況？

想象一個二維例子：

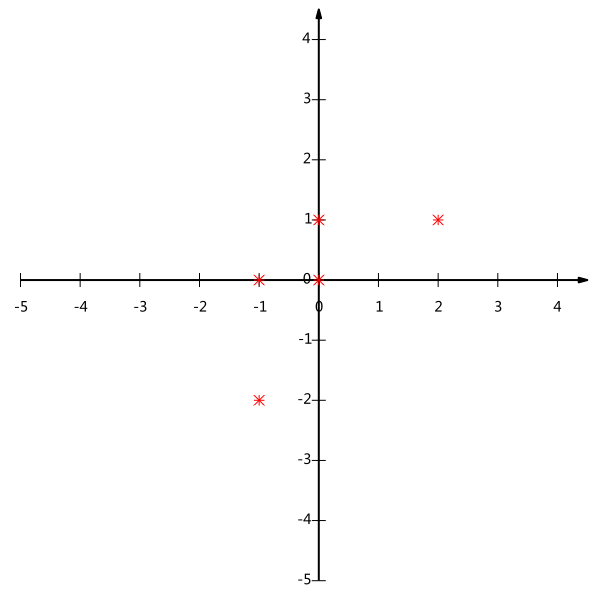
以下這一組樣本，有5個樣本，有2個特徵x和y，矩陣是

[-1,-2]

[-1, 0]

[ 0, 0]

[ 2, 1]

[ 0, 1]

畫圖如下：

我現在是二維特徵表示，x一個特徵，y一個特徵。我現在降維。

降成一維，我要選一個新的基底（特徵）。

如果我選(1,0)作為基底，就是x軸嘛，然後我把這些樣本投影到x軸，或者乘以[1,0]列向量。

得，裡面好幾個數都一樣，分不出來了。

所以這就是為樣本在基底上要儘可能分散了，這個分散不就是樣本在這個“基底上的座標”（這個基底上的特徵值）的方差要儘可能大麼？

（2）第二個要求：使得各個選擇的基底關聯程度最小。

剛才是二維降一維，只選則一個一維基底就可以了，太拿衣服了。

考慮一個三維點投影到二維平面的例子。這樣需要倆基底。

基底得一個一個找啊，先找第一個，要找一個方向，使得樣本在這個方向上方差最大。

再找第二個基底，怎麼找，方差最大？這不還是找的方向和第一個差不多麼？那這兩個方向表示的資訊幾乎是重複的。

所以從直觀上說，讓兩個欄位儘可能表示更多的原始資訊，我們是不希望它們之間存在（線性）相關性的，因為相關性意味著兩個欄位不是完全獨立，必然存在重複表示的資訊。所以最好就是選擇和第一個基底正交的基底。

那怎麼找呢？不能隨便寫一個矩陣吧？答案肯定是要基於原來的樣本的表示。

我們求出了原來樣本的協方差矩陣，協方差矩陣的對角線代表了原來樣本在各個維度上的方差，其他元素代表了各個維度之間的相關關係。

也就是說我們希望優化後的樣本矩陣，它的協方差矩陣，對角線上的值都很大，而對角線以外的元素都為0。

現在我們假設這個樣本矩陣為X（每行對應一個樣本），X對應的協方差矩陣為Cx，而P是我們找到的對樣本進行PCA變換的矩陣，即一組基按列組成的矩陣，我們有Y=XP

Y即為我們變化後的新的樣本表示矩陣，我們設Y的協方差矩陣維Cy，我們想讓協方差矩陣Cy是一個對角陣，那麼我們先來看看Cy的表示

注意：

推導規程為了把X湊一起，我們用了Y Yt=((Y Yt)t)t=(Yt Y)t

把樣本組織成行向量和列向量是一樣的原來，最後結果只需要一個轉置就變成一個格式了。把樣本X組織成列向量，就要把基底P組織成行向量，就要寫PX了

好了，我們退出了Cy的表示，最後的結果很神奇的成了一個熟悉的形式：方陣可對角化的表示式

讓我們來回憶一下可對角化矩陣的定義，順便也回憶了矩陣相似的定義：

（1）什麼是可對角化和相似：如果一個方塊矩陣A相似於對角矩陣，也就是說，如果存在一個可逆矩陣P 使得 P ⁻¹AP 是對角矩陣，則它就被稱為可對角化的。

（2）如何判斷可對角化呢：我們再來回憶一下矩陣可對角化的條件：n × n 矩陣 A 只在域 F 上可對角化的，如果它在 F 中有 n 個不同的特徵值，就是說，如果它的特徵多項式在 F 中有 n 個不同的根，也就說他有n個線性無關的特徵向量，這三條件是等價的，滿足一個就可以對角化。

注意哦：有n個線性無關的特徵向量並不一定代表有n個不同的特徵值，因為可能多個特徵向量的對於空間的權重相同嘛。。。但是n個不同的特徵值一定有n個線性無關的特徵向量啦。

C是啥呢，C是協方差矩陣，協方差矩陣是實對稱矩陣，就是實數的意思，有很多很有用的性質

1）實對稱矩陣不同特徵值對應的特徵向量，不僅是線性無關的，還是正交的。

2）設特徵向量λ重數為r，則必然存在r個線性無關的特徵向量對應於λ，因此可以將這r個特徵向量單位正交化。

3） n階實對稱矩陣C，一定存在一個正交矩陣E，滿足如下式子，即C既相似又合同於對角矩陣。（這裡又溫習了合同的概念哦）

由上面兩條可知，一個n行n列的實對稱矩陣一定可以找到n個單位正交特徵向量，設這n個特徵向量為e1,e2,...,en

我們將其按列組成矩陣：

則對協方差矩陣C有如下結論：

PCA演算法步驟總結：

設有m條n維資料，這裡比較糊塗就是按行組織樣本還是按列組織樣本，下面是按行組織樣本：

1）將原始資料按行組成n行m列矩陣X，代表有n個數據，每個資料m個特徵

2）將X的每一列（代表一個屬性欄位）進行零均值化，即減去這一列的均值

3）求出協方差矩陣C=1/n* XXT

4）求出協方差矩陣的特徵值及對應的特徵向量

5）將特徵向量按對應特徵值大小從上到下按列排列成矩陣，取前k列組成矩陣P

6）Y=XP即為降維到k維後的資料

按列組織是這樣的，理解一下：

1）將原始資料按列組成n行m列矩陣X

2）將X的每一行（代表一個屬性欄位）進行零均值化，即減去這一行的均值

3）求出協方差矩陣C=1/m*XXT
4）求出協方差矩陣的特徵值及對應的特徵向量

5）將特徵向量按對應特徵值大小從上到下按行排列成矩陣，取前k行組成矩陣P

6）Y=PX即為降維到k維後的資料