資料結構之圖(鄰接表儲存,DFS和BFS遍歷)
阿新 • • 發佈:2019-01-24
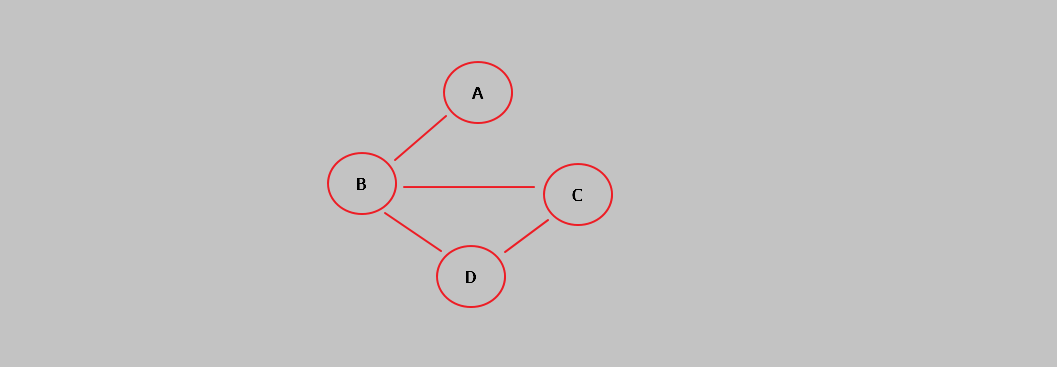
來看下面的一個簡單的圖,
那麼這樣的一個圖,我們應該用什麼儲存結構來儲存它呢?常用的是鄰接矩陣和鄰接表,這裡鄰接矩陣不做講解,如下所有程式碼都是以鄰接表作為儲存結構,所以這裡就只講解下鄰接表。那麼什麼是鄰接表呢?如何構造呢?
鄰接表是一種鏈式儲存。就如上圖,一共有四個頂點(分別是A,B,C,D),鄰接表就是為這四個頂點的每個頂點建立一條單鏈表,也就是四條單鏈表,每個連結串列第一個元素就是該頂點自己。下面就以上面的圖為例,具體介紹如何建立鄰接表。
首先看第一條單鏈表,表頭是頂點A。因為頂點A只與頂點B有鄰接,因此,該單鏈表大概描述為A---->B;
再看第二條單鏈表,表頭是B,而B與A,C,D都有鄰接,故而描述為B----->A------->C------->D;
依次第三條單鏈表為C------>B----->D;
最後第四條單鏈表為D------>B----->C。
現在來理清一下下面程式碼的三個結構體都代表什麼,理清的話,下面的程式碼就很容易理解了。
struct ArcNode { int adjvex; //該弧所指向的頂點的位置 ArcNode * next; //指向下一條弧的指標 //int weight;邊上是否有權 }; typedef struct VNode { char vertex; //頂點資訊 ArcNode * firstarc; //指向第一條依附該頂點的弧的指標 }AdjList[20]; struct ALGraph { AdjList adjList; int vexNum; //圖的頂點數 int arcNum; //圖的弧數 };
看第二個結構體VNode,上面已經說過,對於ABCD四個頂點每個建立一條單鏈表,那麼這四條連結串列該如何管理呢?對的,用陣列,這也就是AdjList[20]的由來(這裡假設一個圖的頂點不超過20個,讀者可以根據自己需求改動)。
第一個結構體ArcNode就是建立連結串列所必需的節點。
那麼最後一個結構體ALGraph就是用來表示一個圖,在一段程式裡,你要做三個圖,就要用這個結構體去申請三個變數,來儲存你的三個圖。
好了,接下來直接看程式碼吧。所有原始碼都已經在下面貼出,沒有遺漏。以下程式碼建立的圖是無向,無權圖,並且使用鄰接表表示圖。部分程式碼參考嚴蔚敏的資料結構。
一:main部分
#include<iostream>
#include<queue>
using namespace std;
struct ArcNode
{
int adjvex; //該弧所指向的頂點的位置
ArcNode * next; //指向下一條弧的指標
//int weight;邊上是否有權
};
typedef struct VNode
{
char vertex; //頂點資訊
ArcNode * firstarc; //指向第一條依附該頂點的弧的指標
}AdjList[20];
struct ALGraph
{
AdjList adjList;
int vexNum; //圖的頂點數
int arcNum; //圖的弧數
};
bool visited[20];//設定標誌陣列
void CreateGraph(ALGraph & graph);
void PrintGraph(ALGraph & graph);
void DFSTraverse(ALGraph & graph);
void BFSTraverse(ALGraph & graph);
int main()
{
/*
8
9
A B C D E F G H
0 1
0 2
1 3
1 4
2 5
2 6
3 7
4 7
5 6
*/
ALGraph graph;
//1.建立鄰接表
CreateGraph(graph);
//2.列印鄰接表
cout << "\n鄰接表列印為: \n";
PrintGraph(graph);
//3.深度優先搜尋DFS
cout << "\n深度優先搜尋DFS: ";
DFSTraverse(graph);
cout << endl;
//4.廣度優先搜尋BFS
cout << "\n廣度優先搜尋BFS: ";
BFSTraverse(graph);
cout << endl<<endl;
return 0;
}二:具體實現
1.構造鄰接表
void CreateGraph(ALGraph & graph)
{
////////1.輸入頂點數和弧數
cout << "請輸入圖的頂點數: ";
cin >> graph.vexNum;
cout << "請輸入圖的弧數: ";
cin >> graph.arcNum;
///////2.輸入頂點資訊
cout << "請輸入" << graph.vexNum << "個頂點資訊: ";
for (int i = 0; i < graph.vexNum; i++)
{
cin >> graph.adjList[i].vertex;
graph.adjList[i].firstarc = nullptr;
}
///////3.根據輸入的弧的資訊構造鄰接表
cout << "請輸入" << graph.arcNum << "個弧的資訊: \n";
int h1, h2;
ArcNode * temp;
for (int i = 0; i < graph.arcNum; i++)
{
cin >> h1 >> h2;
temp = new ArcNode;
temp->adjvex = h2;
temp->next = graph.adjList[h1].firstarc;
graph.adjList[h1].firstarc = temp;
temp = new ArcNode;
temp->adjvex = h1;
temp->next = graph.adjList[h2].firstarc;
graph.adjList[h2].firstarc = temp;
}
}2.列印鄰接表
void PrintGraph(ALGraph & graph)
{
for (int i = 0; i < graph.vexNum; i++)
{
cout << graph.adjList[i].vertex << "------>";
ArcNode * p = graph.adjList[i].firstarc;
while (p)
{
cout << graph.adjList[p->adjvex].vertex << " ";
p = p->next;
}
cout << endl;
}
}3.深度優先搜尋DFS。類似於樹的先序遍歷。假設圖中所有頂點未被訪問,則深度優先遍歷是從某個頂點v開始,訪問完後,接著訪問v的未被訪問的鄰接點,直至遍歷完。
void DFS(ALGraph & graph, int v)
{
visited[v] = true;
cout << graph.adjList[v].vertex << " ";
ArcNode * p = graph.adjList[v].firstarc;
while (p)
{
if (!visited[p->adjvex])
DFS(graph, p->adjvex);
p = p->next;
}
}
void DFSTraverse(ALGraph & graph)
{
for (int i = 0; i < graph.vexNum; i++)//初始化訪問標誌陣列
visited[i] = false;
for (int i = 0; i < graph.vexNum; i++)
{
if (!visited[i])//如果沒有訪問
DFS(graph, i);
}
}4.廣度優先搜尋BFS。類似於樹的層次遍歷。假設圖中所有頂點未被訪問,則廣度優先遍歷是從某個頂點v開始,訪問後,接著訪問v的未被訪問的鄰接點,然後分別從這些鄰接點開始依次訪問它們的鄰接點(因此用到了佇列),直至遍歷完。
void BFSTraverse(ALGraph & graph)
{
for (int i = 0; i < graph.vexNum; i++)//初始化訪問標誌陣列
visited[i] = false;
queue<int> q;
for (int i = 0; i < graph.vexNum; i++)
{
if (!visited[i])//如果沒有訪問過
{
visited[i] = true;
q.push(i);//訪問過的入佇列
cout << graph.adjList[i].vertex << " ";
while (!q.empty())//佇列不為空時
{
int x = q.front();
q.pop();//先取出隊首第一個元素,然後將第一個元素刪除
ArcNode * p = graph.adjList[x].firstarc;
while (p)//訪問未被訪問過的鄰接頂點
{
if (!visited[p->adjvex])
{
visited[p->adjvex] = true;
cout << graph.adjList[p->adjvex].vertex << " ";
q.push(p->adjvex);
}
p = p->next;
}
}
}
}
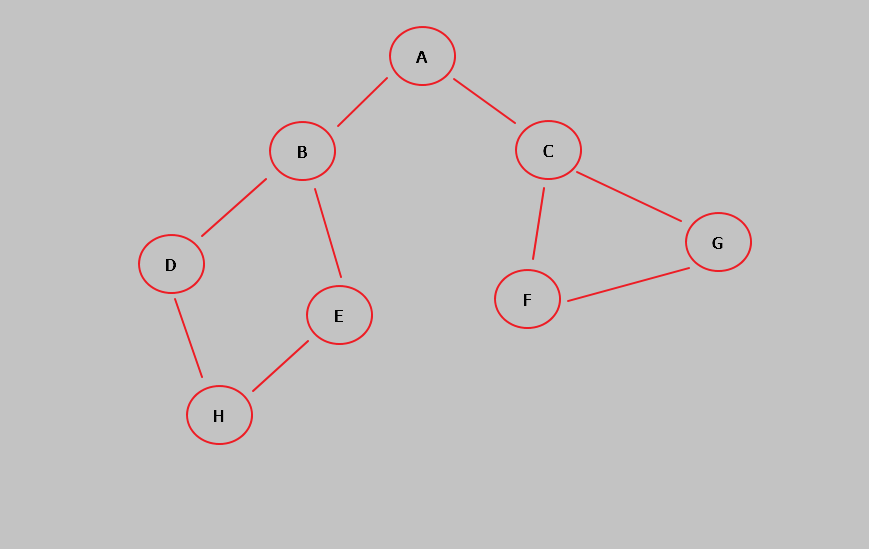
}三:資料測試
其中上述資料建立的圖的結構如下圖: