今天介紹一下NormFace: L2 Hypersphere Embedding for Face Verification

Motivation

希望利用正則化解決兩個問題：1. 人臉識別任務裡面的loss有softmax、contrastive、triplet、pairwise等等，其中softmax是單個樣本輸入就可以訓練的，其他的都是需要sample的，尤其是metric-learning每次要sample 3個樣本才能算出一個loss，這會導致取樣空間為N^3，速度慢而且取樣策略對訓練結果影響很大；2. softmax本身優化的是沒有歸一化的內積結果，但是最後在預測的時候使用的一般是cosine距離或者歐式距離，這會導致優化目標和最終的距離度量其實並不一致。我們之前做的時候用softmax訓練做pretrain，然後後面用歐式距離的metric-learning做進一步學習或者finetune其實也是不大合理的，用一個歐式距離優化目標去finetune一個內積空間最優的模型應該不容易得到好的效果。

基本原理

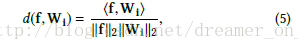既然最後在特徵對比的時候使用歸一化的cosine距離，那麼就在訓練的時候也把feature做歸一化處理，即 ，其中e是為了防止除0的較小正數。 對應的BP求導公式： 為了解釋一下為什麼需要normalize，作者還做了比較漂亮的數學推導並給出了視覺化的結果。softmax loss傾向於學習到一個radial分佈的特徵，其原因在於特徵的scale越大就會使得softmax的loss越小，figure.3裡面是softmax之前的fc有bias的情況下會使得有些類別在角度上沒有區分性但是通過bias可以區分，在這種情況下如果對feature做normalize，會使得中間的那個小類別的feature變成一個單位球形並與其他的feature重疊在一起，所以在feature normalize的時候是不能加bias的。 做了歸一化之後，softmax的優化就變成了直接優化cosine距離了： 但是這裡有遇到一個問題是這樣訓練並不收斂，其原因在於normalize之後softmax loss的輸入處於一個[-1,1]的分佈，其最小值被抑制、是有下限的，並且對於一個類別的概率來說，其公式為：，

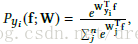即使樣本被完美分類，即對應類別的輸出為1，其他的為-1，那麼這個概率Py還是一個比較小的值，而softmax loss的梯度為1-Py，這使得容易的樣本梯度也很大。相比於原來的softmax loss，其輸入的scale可以很大使得概率Py是個接近於1的數使得難易樣本的梯度差別比較明顯。所以解決辦法也就顯而易見了，就是在normalize之後加個scale，讓這個差距再拉大，所以最終normalize之後的softmax loss如下，其中w和f都是歸一化的。

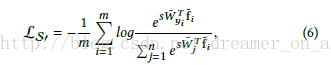
到這裡為止作者已經解決了歸一化的softmax問題，那麼歸一化還有什麼好處呢，由於歸一化之後w和f的平方項為1或者常數，

那麼歐式距離、內積、cosine距離就變成了等價的

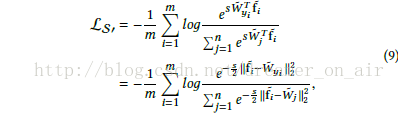所以contrastive和metric-learning也可以寫成單樣本形式：

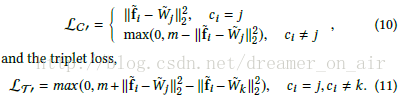
其原理在於用Wj、Wk去代替原本loss裡面的fj和fk，作者把這個Wj叫做第j類feature的agent，

直觀的理解就是fi和他自己所在類別的Wj的距離應該足夠接近而與其他類別的Wk的距離應該足夠遠，

其實這個與原本的constractive和triplet loss還是有本質差別的，這裡的loss輸入仍然是f和W內積之後的輸出，

只不過形式變成了不同類別所對應的輸出之間的比較，而原來在沒有normalize的情況下這個值並不能等價

於cosine距離並且範圍不固定使得margin的選擇變得很困難。相比於作者之前的工作

SphereFace: Deep Hypersphere Embedding for Face Recognition. In Proceedings of the IEEE conference on computer vision

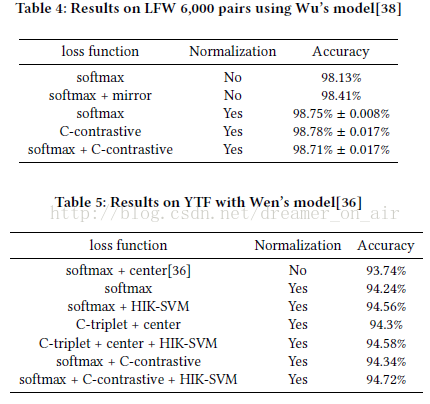
and pattern recognition，除了做weight normalize之外還做了feature normalize， 並由此設計了一些分類任務也可以實現的intra&inter classloss。

實驗結果

相比於前面的推演，實驗結果有點讓人失望，結論是normalize本身比loss的區別更重要， 而且提升也不是特別明顯。其中有一些trick作者在文章裡提到的： 1. 歸一化feature的時候scale是十分必要的但是歸一化weight的時候並不需要scale， 從原理上來看最終是W和f的內積，所以任何一方有scale應該都是可以的， 所以作者也沒能解釋這個原因是什麼，有分析明白的朋友可以幫忙解釋一下？ 2. finetune要比from scratch要好，其中from scratch做weight normalize訓練無法收斂。

總結：

數學上的工作比較漂亮，normalize本身對於深度學習的訓練有好處這個事情其實已經是共識， 在normalize之後用內積的方式構造了contrastive、triplet、centerloss的idea是很新穎的， 但是當類別數較多的時候，比如1000萬類，還是會遇到softmax一樣的超大W視訊記憶體問題， 還是得用傳統的triplet loss。另外就是在實際計算triplet的時候作者沒有提到取樣之類的問題， 雖然變成了單樣本模式，但是f與哪些Wj和Wk計算distance貌似沒有提， 如果都算的話計算量比較大而且並沒有hard negtive samping在裡面，這可能也是導致結果在新提出的loss上並沒有變好的原因。