一元線性迴歸(原理)
阿新 • • 發佈:2019-01-25
前言:
一元線性迴歸是資料探勘的基礎模型,其中包含了非常重要的數學回歸的概念,是學習多元迴歸,廣義線性迴歸的基礎。本文主要講解1)基礎原理2)數學推導3)R語言演示,來介紹一元線性迴歸。
關鍵詞:一元線性迴歸基礎原理、最小二乘法、數學推導、R語言
整體思路:
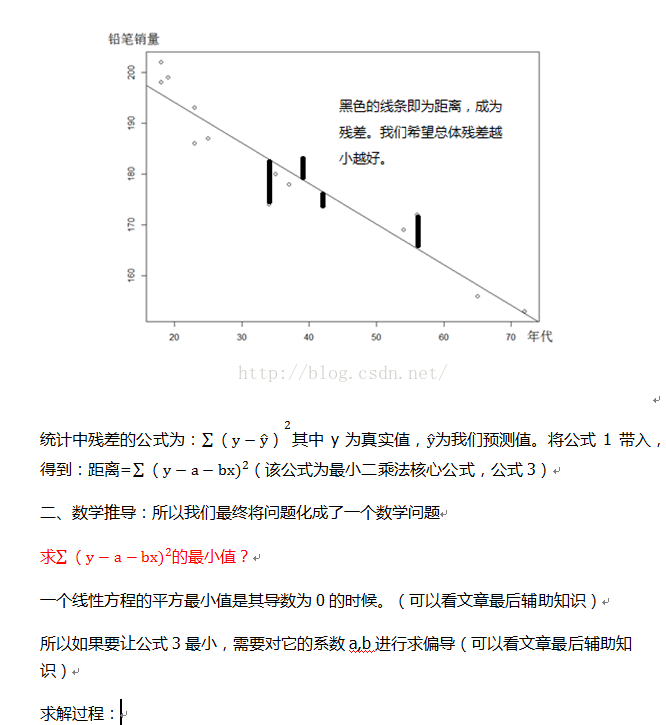
根據已知點求一條直線,希望直線與各個點距離之和為最小,根據最小二乘法算出最小時直線的引數。
正文:
一、基礎原理:假設已知鉛筆銷量和時代的關係,如下圖散點:
三、R語言實現:
> x = c(18,23,25,35,65,54,34,56,72,19,23,42,18,39,37)
>y=c(202,186,187,180,156,169,174,172,153,199,193,174,198,183,178)
> plot(x,y)#繪散點圖
> fm = lm(y ~ x) #擬合線性迴歸模型
> abline(fm) #繪製(新增)迴歸線
輔助知識:
求導的目的是求一個公式的變化率。比如y=x^2 求導後為 y=2x ,即當X=0時它的變化率是最低。(斜率為0),隨著X增大1個單位,y的變化速度就增加2個單位的速度。如果x=10,y的增幅變化率就是20.可以自己想想一下y=x^2的圖形就明白了。
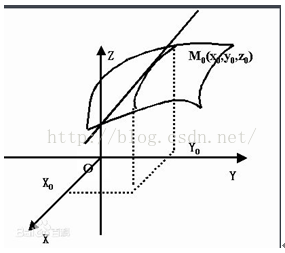
偏導:在一元函式中,我們已經知道導數就是函式的變化率。對於二元函式我們同樣要研究它的“變化率”。所以就分別對每個元素進行求導,稱為偏導。參考資料:
《R語言統計分析軟體簡明教程》 王斌會等
百度百科